If Abc Dbc Then B Is The Midpoint Of Ad
Breaking News Today
Jun 02, 2025 · 5 min read
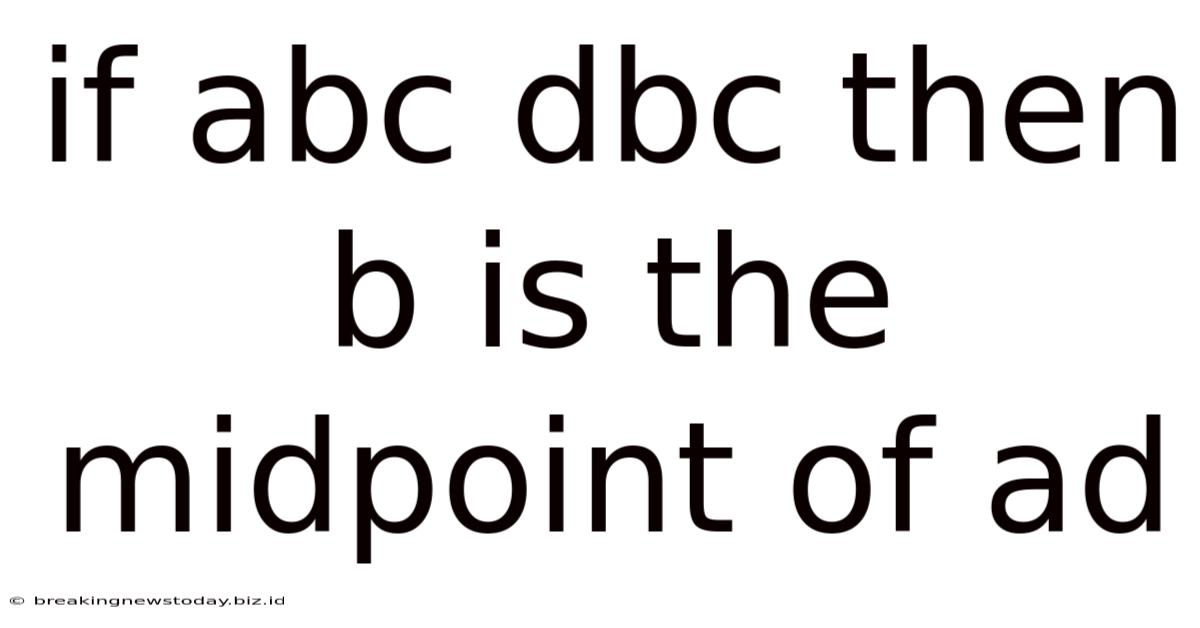
Table of Contents
If AB = BC, then B is the Midpoint of AC: A Comprehensive Exploration
This article delves into the geometrical concept proving that if the length of line segment AB is equal to the length of line segment BC, then point B is the midpoint of line segment AC. We will explore various approaches to proving this fundamental theorem, examining its implications and applications in different contexts. This exploration will be suitable for students of geometry, mathematics enthusiasts, and anyone looking for a deeper understanding of this essential geometric principle.
Understanding the Midpoint Theorem
The midpoint theorem states that a point B is the midpoint of a line segment AC if and only if the distance from A to B is equal to the distance from B to C. In simpler terms: AB = BC. This seemingly simple statement forms the basis for many more complex geometrical proofs and constructions.
This isn't just a theoretical concept; it's a foundational principle used extensively in:
- Coordinate Geometry: Determining the coordinates of midpoints given the coordinates of endpoints.
- Construction Geometry: Accurately bisecting line segments using compasses and straightedges.
- Advanced Geometry: Used as a stepping stone for more complex theorems and proofs involving triangles, circles, and other shapes.
- Real-World Applications: Finding the center of objects, determining equilibrium points, and other practical applications in engineering and design.
Proof Methods: Demonstrating AB = BC Implies B is the Midpoint of AC
We can prove the midpoint theorem using several methods. Let's explore a few:
1. The Distance Formula (Coordinate Geometry Approach)
Let's assume we have two points A and C on a Cartesian coordinate plane. Let the coordinates of A be (x₁, y₁) and the coordinates of C be (x₂, y₂). If B is the midpoint of AC, its coordinates would be:
B = ((x₁ + x₂)/2, (y₁ + y₂)/2)
The distance formula calculates the distance between two points (x₁, y₁) and (x₂, y₂) as:
√((x₂ - x₁)² + (y₂ - y₁)²)
Now, let's calculate the distances AB and BC:
AB = √(((x₁ + x₂)/2 - x₁)² + ((y₁ + y₂)/2 - y₁)²) = √(((x₂ - x₁)/2)² + ((y₂ - y₁)/2)²) = (1/2)√((x₂ - x₁)² + (y₂ - y₁)²)
BC = √(x₂ - (x₁ + x₂)/2)² + (y₂ - (y₁ + y₂)/2)²) = √(((x₂ - x₁)/2)² + ((y₂ - y₁)/2)²) = (1/2)√((x₂ - x₁)² + (y₂ - y₁)²)
As you can see, AB = BC. This demonstrates that if B is the midpoint, then AB = BC. The reverse is also true: If AB = BC, then B is the midpoint.
2. Geometric Approach: Using Congruent Triangles
This method employs the principles of congruent triangles. Let's imagine a line segment AC. Point B lies on AC such that AB = BC. Now, let's construct a perpendicular bisector of AC, intersecting AC at point M. This bisector divides AC into two equal halves, AM = MC.
Consider two right-angled triangles: △AMB and △CMB. We know that:
- AB = BC (given)
- AM = MC (by construction of the perpendicular bisector)
- ∠AMB = ∠CMB = 90° (by construction)
By the Side-Angle-Side (SAS) postulate of congruent triangles, △AMB ≅ △CMB. Since these triangles are congruent, their corresponding sides are equal, and therefore, M must coincide with B. Consequently, B is the midpoint of AC.
3. Vector Approach
Using vectors, let's represent the position vectors of points A, B, and C as a, b, and c, respectively. If B is the midpoint of AC, then the vector from A to C can be represented as c - a. The midpoint B can be expressed as:
b = a + (1/2)(c - a) = (a + c)/2
The vector AB is b - a = (a + c)/2 - a = (c - a)/2
The vector BC is c - b = c - (a + c)/2 = (c - a)/2
Therefore, the magnitude of vector AB equals the magnitude of vector BC, showing that AB = BC. Again, the reverse holds true; if AB = BC, then B is the midpoint.
Implications and Applications
The seemingly simple theorem of AB = BC implying B is the midpoint of AC has significant implications in various fields:
1. Construction and Design
In architecture, engineering, and design, accurately determining midpoints is crucial for creating symmetrical and balanced structures. From building bridges to designing logos, the concept of the midpoint ensures precision and aesthetic appeal.
2. Computer Graphics and Programming
Midpoint calculations are fundamental in computer graphics and programming. They are used for things such as:
- Line drawing algorithms: Efficiently rendering lines on a screen.
- Interpolation: Smoothing curves and surfaces.
- 3D modeling: Precisely placing points and vertices in three-dimensional space.
3. Navigation and Surveying
In navigation and surveying, finding the midpoint is essential for calculating distances and locations. Midpoint calculations help determine the center of a geographical area, the midpoint of a journey, or the precise location of an object.
4. Physics and Engineering
The midpoint theorem plays a role in physics and engineering calculations, such as:
- Center of mass: Calculating the centroid of an object.
- Equilibrium points: Determining points of balance or stability in a system.
- Moments and forces: Analysis of forces acting on objects.
Advanced Considerations
The concept extends beyond simple line segments. Similar principles apply to more complex geometrical shapes and situations. For instance:
- Midpoint of a curve: Approximating the midpoint of a curved line using numerical methods.
- Midpoint in higher dimensions: Extending the concept to three or more dimensions.
- Midpoint theorem in non-Euclidean geometries: Exploring variations of the midpoint theorem in spaces that don't adhere to Euclidean axioms.
Conclusion
The theorem "If AB = BC, then B is the midpoint of AC" is a foundational concept in geometry with wide-ranging applications across numerous disciplines. We have explored various approaches to proving this theorem, highlighting its importance in both theoretical mathematics and practical applications. Understanding this principle solidifies a critical understanding of geometry and lays the groundwork for tackling more advanced geometrical problems and real-world challenges. The simplicity of the theorem belies its immense power and significance in the world of mathematics and beyond.
Latest Posts
Latest Posts
-
Select The Text That Has A More Objective Tone
Jun 04, 2025
-
The Passage Implies That The Icebox Of The Nation Slogan
Jun 04, 2025
-
Sarah Sights The Top Of The Statue Of Liberty
Jun 04, 2025
-
Which Describes Oxygen Content As Earth Evolved Over Time
Jun 04, 2025
-
A Student Drew The Following Flowchart
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about If Abc Dbc Then B Is The Midpoint Of Ad . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.