If Ef Bisects Cd Cg 5x 1
Breaking News Today
Jun 04, 2025 · 5 min read
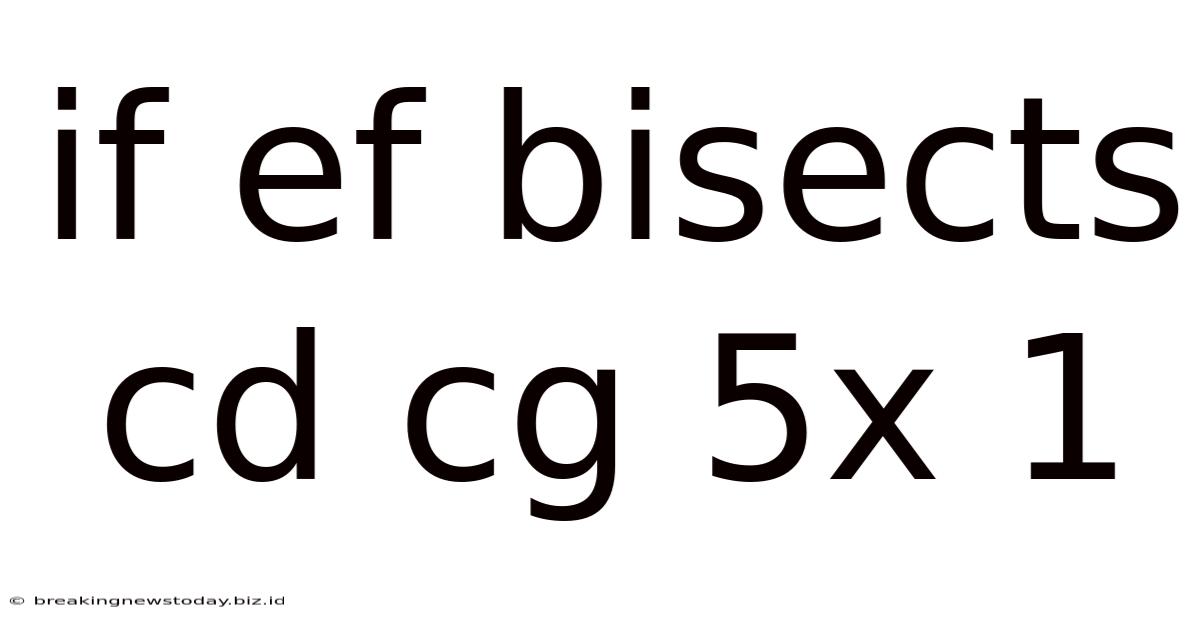
Table of Contents
If EF bisects CD, CG = 5x + 1... Solving Geometry Problems
This article delves into the world of geometry, specifically exploring problems involving bisectors and how to solve them systematically. We'll unpack the given statement "If EF bisects CD, CG = 5x + 1..." and demonstrate how to approach similar problems, emphasizing the importance of understanding geometric principles and utilizing algebraic techniques. This will cover various scenarios and problem-solving strategies to equip you with the skills to tackle a wide range of geometry challenges. We'll also touch upon the application of these concepts in real-world situations.
Understanding the Problem: Bisectors and Segments
Before we dive into the specifics, let's clarify some key terms. A bisector is a line, segment, or ray that divides a line segment or an angle into two equal parts. In our problem, we're told that EF bisects CD. This means that EF intersects CD at a point, let's call it G, such that CG = GD. The statement "CG = 5x + 1" gives us an algebraic expression for the length of segment CG.
To solve this kind of problem, we'll almost always need more information. The problem statement, as it stands, is incomplete. We need additional information about the lengths of other segments, angles formed, or relationships between different parts of the figure to find the value of x and the lengths of the segments.
Scenario 1: Introducing Additional Information
Let's assume, for our first scenario, that we are given an additional piece of information: GD = 3x + 7. Since EF bisects CD, we know that CG = GD. Therefore, we can set up an equation:
5x + 1 = 3x + 7
Solving for x:
2x = 6 x = 3
Now that we have the value of x, we can find the lengths of CG and GD:
CG = 5x + 1 = 5(3) + 1 = 16 GD = 3x + 7 = 3(3) + 7 = 16
Therefore, CG = GD = 16. The length of CD is 32 (CG + GD).
Scenario 2: Incorporating Angles
Let's consider a different scenario where instead of another segment length, we are given information about angles. Suppose we know that angle CGE is a right angle (90 degrees) and angle DGF is also a right angle (90 degrees). Furthermore, suppose we are given that EG = 8. This information, while not directly involving the lengths of CG and GD, could be relevant depending on the overall geometric figure. For example, if the complete figure is a rectangle or square, knowing that CG = GD allows us to understand the relationship between the sides.
In this case, the information provided, while potentially useful in a larger context, doesn’t directly help us solve for x. We would require additional data, possibly relationships between segments CG and EG, or information about another segment within the complete geometric figure.
Scenario 3: Introducing Triangles
Let's imagine the segment CD is part of a larger triangle. Let’s assume that points C, G, and another point, H, form a right-angled triangle, with the right angle at G. Let's say we are given the length of CH = 20. We can then use the Pythagorean theorem (a² + b² = c²) to solve for x. However, we'd need additional information linking CG and GH to solve the problem using this approach. Simply knowing CG = 5x + 1, and CH is not enough to solve for x.
General Problem Solving Strategies for Geometry
Solving geometry problems often involves a combination of geometric principles and algebraic techniques. Here's a step-by-step approach:
-
Draw a diagram: Always start by drawing a clear diagram of the given information. This helps visualize the problem and identify relevant relationships.
-
Identify relevant theorems and postulates: Recall the geometrical theorems and postulates that might be applicable to the problem. This could include the Pythagorean theorem, properties of bisectors, angle relationships in triangles, properties of parallel lines, and more.
-
Set up equations: Based on the diagram and the identified theorems/postulates, set up equations that relate the given information.
-
Solve the equations: Use algebraic techniques to solve the equations and find the unknown values.
-
Check your solution: Always check your solution to make sure it's consistent with the given information and the diagram.
Real-World Applications of Geometry and Bisectors
The concept of bisectors and related geometrical principles have numerous real-world applications:
-
Architecture and Construction: Bisectors are used extensively in architectural and construction designs for creating symmetrical structures, dividing spaces efficiently, and ensuring precise measurements.
-
Engineering: In engineering, bisectors are important in designing structures, calculating distances, and solving problems related to angles and measurements.
-
Cartography (Mapmaking): Bisectors play a role in creating accurate maps and calculating distances and areas.
-
Computer Graphics and Game Development: Bisectors are fundamental to creating computer graphics and game design, helping to create symmetrical shapes, calculate angles, and optimize graphics rendering.
Advanced Techniques and Considerations
For more complex problems, you might need to use more advanced techniques like coordinate geometry, vectors, or trigonometric functions. These techniques enable you to deal with geometric problems in a more analytical and abstract way.
Conclusion:
The statement "If EF bisects CD, CG = 5x + 1..." itself is insufficient to solve for x. It requires additional information about other lengths, angles, or relationships within the geometric figure. Understanding bisectors and applying geometric principles in conjunction with algebraic techniques are essential for tackling such problems. Remember to always visualize the problem with a diagram, identify relevant theorems, set up equations systematically, and verify your solutions. The problem-solving strategies discussed here, along with a firm grasp of geometric concepts, will equip you to solve a wide variety of geometry challenges, both simple and complex. Remember to always practice and expand your knowledge base to become proficient in this field.
Latest Posts
Latest Posts
-
The Healthfulness Of A Food Is Best Described As Its
Jun 06, 2025
-
Using A An Statement When Saying No
Jun 06, 2025
-
Which Of The Following Characterizes An Exchange
Jun 06, 2025
-
For A Certain Rectangular Region The Ratio
Jun 06, 2025
-
The Four Ss In The Vehicle Movement Checklist Are
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about If Ef Bisects Cd Cg 5x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.