Lin Multiplies 7/8 Times A Number
Breaking News Today
Jun 01, 2025 · 5 min read
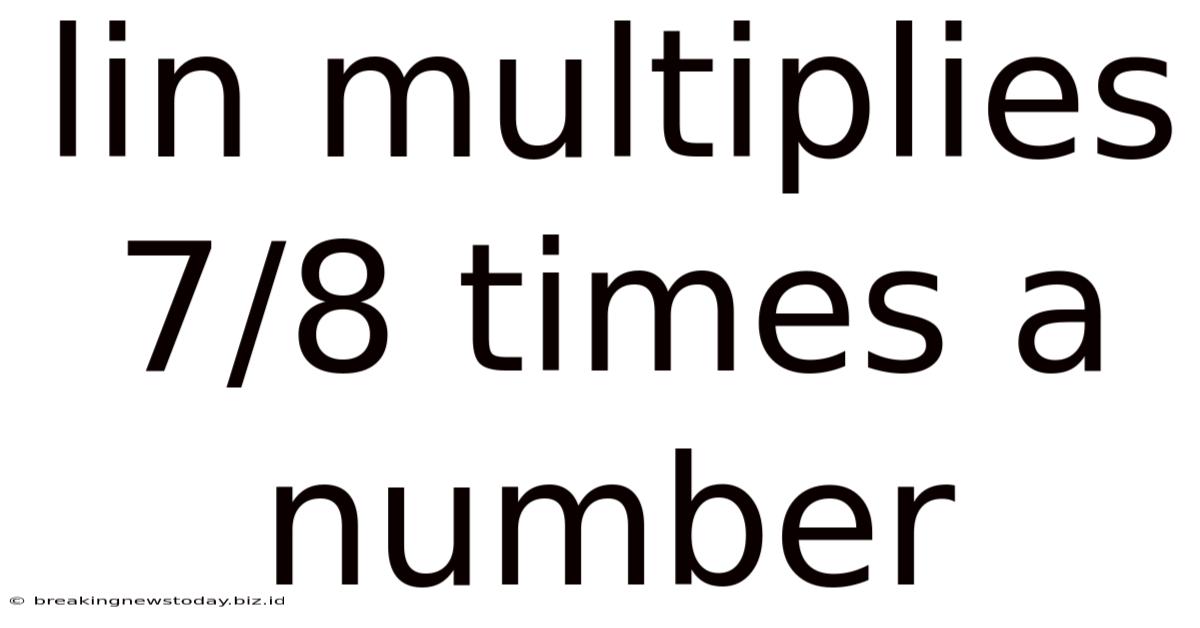
Table of Contents
Lin Multiplies 7/8 Times a Number: A Deep Dive into Fractions and Algebra
This article explores the mathematical problem where Lin multiplies a number by 7/8, examining the various ways to solve this, the underlying mathematical concepts, and how to apply this to similar problems. We'll delve into the intricacies of fractions, algebraic representation, and practical applications, aiming to provide a comprehensive understanding for students and anyone interested in strengthening their mathematical skills.
Understanding the Problem: Lin's Multiplication
The core of the problem lies in understanding the phrase "Lin multiplies 7/8 times a number." This translates directly into a mathematical expression. Let's represent the unknown number as 'x'. The problem can then be written as:
(7/8) * x
or more simply:
7x/8
This expression signifies that Lin is taking seven-eighths of the unknown number 'x'. This seemingly simple problem opens doors to exploring various mathematical concepts and techniques for finding a solution.
Solving for 'x': Different Approaches
The solution hinges on knowing either the result of Lin's multiplication or having additional information relating to 'x'. Let's explore several scenarios and their respective solutions:
Scenario 1: The Result is Known
Let's assume the result of Lin's multiplication is a known value, say 'y'. Our equation then becomes:
7x/8 = y
To solve for 'x', we follow these steps:
-
Multiply both sides by 8: This eliminates the denominator, resulting in: 7x = 8y
-
Divide both sides by 7: This isolates 'x', giving us the solution: x = 8y/7
This formula allows us to find the original number 'x' if we know the result 'y' of Lin's multiplication. For example, if y = 56, then x = (8 * 56) / 7 = 64.
Scenario 2: Additional Information about 'x'
Suppose we know that 'x' is related to another variable or has a specific property. Let's consider a few examples:
-
x is 16 more than another number 'z': If x = z + 16, we substitute this into our original equation: (7/8)(z + 16) = y. Solving this requires expanding the brackets and then following the steps outlined in Scenario 1.
-
x is a multiple of 8: If x is a multiple of 8, we can represent it as x = 8k, where k is an integer. Substituting this into the equation gives us (7/8)(8k) = y, which simplifies to 7k = y. This means that the result 'y' will always be a multiple of 7.
-
x is a fraction: If x is a fraction, say a/b, the equation becomes (7/8)(a/b) = y. This can be simplified to 7a/8b = y and solved for 'a' or 'b' depending on what is known.
These scenarios highlight the importance of understanding the context of the problem to devise an appropriate solution.
Deep Dive into Fraction Multiplication
The problem inherently involves fraction multiplication. Understanding this operation is crucial for accurately solving the problem. When multiplying fractions, we multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(a/b) * (c/d) = (a * c) / (b * d)
In Lin's problem, we have (7/8) * x. If x were also a fraction, say p/q, the multiplication would be:
(7/8) * (p/q) = (7p) / (8q)
This demonstrates the straightforward nature of fraction multiplication, a fundamental concept necessary for solving algebraic equations involving fractions.
Algebraic Representation and Manipulation
The problem beautifully illustrates the power of algebraic representation. Expressing the problem as an equation (7x/8 = y) allows for systematic manipulation to isolate the unknown variable 'x'. This is a cornerstone of algebra, enabling the solution of a wide array of problems. The process of solving for 'x' involves applying the principles of inverse operations:
- Multiplication's inverse is division: We divide both sides by 7 to counteract the multiplication by 7.
- Division's inverse is multiplication: We multiply both sides by 8 to counteract the division by 8.
This methodical approach highlights the elegance and precision of algebraic manipulation.
Real-World Applications
The concept of multiplying a number by a fraction has numerous practical applications:
-
Calculating discounts: A 12.5% discount can be expressed as 1/8. Calculating the discounted price involves multiplying the original price by 7/8.
-
Portioning ingredients: Recipes often require fractional amounts of ingredients. If a recipe calls for 7/8 of a cup of flour, and you want to make a larger batch, you'll multiply this fraction by the scaling factor.
-
Determining percentages: Multiplying a number by 7/8 is equivalent to calculating 87.5% of that number. This is useful in various scenarios, including calculating sales tax, commission, or grades.
-
Scaling dimensions: In design or construction, scaling dimensions often involves multiplying lengths or areas by fractions.
-
Financial calculations: Interest calculations and determining portions of investments often require manipulating fractions.
Expanding the Problem: More Complex Scenarios
Let's explore more complex variations of Lin's problem to further enhance our understanding:
-
Adding or subtracting fractions: The problem could be extended to include additional fractions. For example, what if Lin adds 1/4 to the result of multiplying a number by 7/8? This would create an equation like: (7x/8) + (1/4) = y. Solving this requires careful manipulation of fractions.
-
Multiple unknown variables: The problem could involve multiple unknown variables. For example, if Lin multiplies two unknown numbers, x and y, by 7/8 and the result is z, then the equation becomes (7/8)xy = z. Solving this requires additional information.
-
Using inequalities: Instead of an equality, we could introduce an inequality. For example, (7/8)x > y. This would lead to solving for a range of values for x rather than a single value.
These expanded scenarios demonstrate how the basic principles of fraction multiplication and algebraic manipulation can be applied to more intricate mathematical problems.
Conclusion: Mastering Fractions and Algebra
Lin's simple problem of multiplying a number by 7/8 provides a gateway to understanding fundamental concepts in fractions and algebra. By analyzing various scenarios, exploring different solution methods, and understanding real-world applications, we have gained a deeper appreciation for the power and versatility of these mathematical tools. Mastering these concepts is not only crucial for academic success but also essential for navigating numerous practical situations. Through continued practice and exploration, one can confidently tackle even the most complex problems involving fractions and algebraic manipulation. The journey from a simple multiplication problem to a comprehensive understanding of its underlying mathematical principles demonstrates the beauty and practicality of mathematics in our everyday lives.
Latest Posts
Latest Posts
-
What Type Of Tubing Flare Is Shown In This Illustration
Jun 02, 2025
-
0 04 Is 10 Times As Great As Which Decimal
Jun 02, 2025
-
What Is Twisted In An Angular Misalignment
Jun 02, 2025
-
True Or False Schuberts Song Melodies Focused On Religious Themes
Jun 02, 2025
-
The Most Visible Indication Of Oversight Is The
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about Lin Multiplies 7/8 Times A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.