Match Each Type Of Factorial Design To The Correct Definition.
Breaking News Today
Apr 04, 2025 · 6 min read
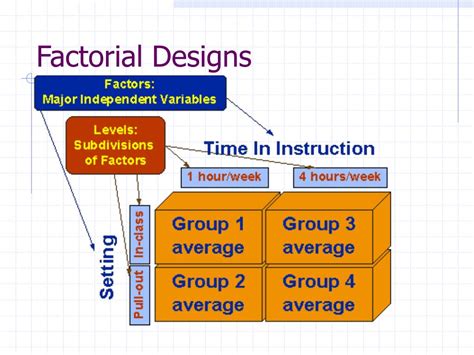
Table of Contents
Matching Factorial Designs to Their Definitions: A Comprehensive Guide
Factorial designs are a cornerstone of experimental design, allowing researchers to investigate the effects of multiple independent variables (factors) simultaneously. Understanding the nuances of different factorial designs is crucial for conducting rigorous and insightful experiments. This comprehensive guide provides clear definitions for various factorial designs, highlighting their strengths and weaknesses, and offering practical examples to solidify your understanding.
What is a Factorial Design?
Before diving into specific types, let's establish a foundational understanding. A factorial design is an experimental design where two or more independent variables are manipulated to observe their effects on a dependent variable. The key characteristic is that all possible combinations of the independent variables' levels are included in the experiment. This allows researchers to assess not only the main effects of each independent variable but also the interactions between them. Interactions occur when the effect of one independent variable depends on the level of another.
Types of Factorial Designs and Their Definitions:
We'll explore several common types, categorized by their structure and complexity:
1. Completely Randomized Factorial Design (CRF):
Definition: This is the simplest form of a factorial design. Subjects (or experimental units) are randomly assigned to each combination of the independent variable levels. This randomization ensures that any differences observed between groups are likely due to the manipulation of the independent variables, rather than pre-existing differences between subjects.
Strengths: Simple to implement and analyze. Provides unbiased estimates of main effects and interactions.
Weaknesses: Can be inefficient if there are many factors or levels, requiring a large number of subjects. Doesn't control for confounding variables beyond random assignment.
Example: Imagine studying the effect of fertilizer type (Factor A: Organic vs. Chemical) and watering frequency (Factor B: Daily vs. Weekly) on plant growth (dependent variable). A CRF would randomly assign plants to each of the four possible combinations (Organic & Daily, Organic & Weekly, Chemical & Daily, Chemical & Weekly).
2. Randomized Block Design (RBD):
Definition: This design introduces a blocking factor to control for a known source of variation. Subjects are first grouped into blocks based on this blocking factor, and then randomly assigned to the treatment combinations within each block. This reduces the error variance and increases the power of the experiment.
Strengths: More efficient than CRF when a significant source of variation exists. Reduces experimental error.
Weaknesses: Requires identification of a relevant blocking factor. Analysis is slightly more complex than CRF.
Example: Continuing with the plant growth example, if the plants are grown in different sections of a greenhouse with varying sunlight exposure, sunlight could be the blocking factor. Plants within each section are then randomly assigned to the fertilizer and watering combinations.
3. Nested Factorial Design (Hierarchical Design):
Definition: This design is used when one factor is nested within another. This means that the levels of one factor are only meaningful within a specific level of the other factor.
Strengths: Appropriate for hierarchical structures, like studying the effect of teachers (Factor A) and students within each teacher (Factor B, nested within A).
Weaknesses: More complex analysis compared to CRF and RBD.
Example: Evaluating the teaching methods (Factor A) used by different teachers (Factor A levels). Student performance (dependent variable) is measured, and student is nested within teacher – different teachers have different sets of students.
4. Split-Plot Factorial Design:
Definition: This design is used when it's impractical or impossible to randomize the levels of one or more factors across all experimental units. One factor is applied to larger "whole plots," while the other factor is applied to smaller "subplots" within each whole plot.
Strengths: Allows for the investigation of factors that are difficult or impossible to randomly assign.
Weaknesses: More complex analysis due to the presence of whole plot and subplot error terms.
Example: Studying the effect of different irrigation systems (Factor A, applied to whole plots of land) and fertilizer types (Factor B, applied to subplots within each irrigation system).
5. Latin Square Design:
Definition: A Latin square design is used to control for two sources of variation, reducing experimental error. It's a special case of a factorial design where the number of levels of each factor is the same, and each level of one factor appears only once in each row and column.
Strengths: Efficient in controlling for two nuisance variables.
Weaknesses: Requires an equal number of levels for all factors. The analysis is more complex than simpler factorial designs.
Example: Testing different types of car tires (Factor A), driven on different road surfaces (Factor B), and by different drivers (Factor C).
6. Fractional Factorial Designs:
Definition: These designs are used when the full factorial design is too large or expensive to conduct. Only a fraction of the possible combinations of factor levels are included in the experiment.
Strengths: Significant reduction in the number of experimental runs. Cost-effective.
Weaknesses: Some information on main effects and interactions may be lost. Requires careful planning to ensure that important effects can be estimated. Analysis requires specialized techniques.
Example: In a situation with many factors (e.g., studying the influence of five factors on product yield), a full factorial design would require 2<sup>5</sup> = 32 runs. A fractional factorial design might only require a fraction of those runs, for example 16 runs or less, still providing valuable insights.
7. Repeated Measures Factorial Design:
Definition: In this design, the same subjects are measured under all combinations of the independent variable levels. This reduces the error variance by controlling for individual differences between subjects.
Strengths: Increased statistical power compared to designs without repeated measures. Fewer subjects are needed.
Weaknesses: Can lead to carry-over effects if the order of treatment conditions is not carefully controlled. Analysis requires specialized techniques that account for the repeated measures nature of the data.
Example: Measuring reaction time (dependent variable) under different levels of caffeine (Factor A) and different task complexities (Factor B) in the same group of participants.
Choosing the Right Factorial Design:
The selection of the appropriate factorial design depends on several factors:
- Number of factors and levels: Simple designs are suitable for fewer factors and levels. More complex designs are needed for larger studies.
- Resources: The availability of resources (time, subjects, materials) influences the feasibility of different designs.
- Presence of confounding variables: Blocking or other control strategies may be necessary to address confounding variables.
- Research question: The specific research question dictates the structure of the experiment.
Beyond the Basics: Advanced Considerations
The designs discussed above represent the core types. However, the field of experimental design is rich and diverse. Variations and combinations of these designs exist, further enhancing their flexibility and applicability to various research contexts. For instance, you might encounter mixed-model designs where some factors are between-subjects and others are within-subjects.
Mastering factorial designs requires a thorough understanding of statistical principles and careful consideration of the specific research question. This guide provides a foundational overview to help you choose and implement the most appropriate design for your experimental needs. Remember that consulting with a statistician is highly recommended, especially for complex designs or intricate analyses. Proper design planning minimizes error, maximizes statistical power, and ultimately leads to more robust and reliable research conclusions.
Latest Posts
Latest Posts
-
What Value Of X Will Make Parallelogram Abcd A Rhombus
Apr 05, 2025
-
In The Conclusion Of An Argumentative Essay The Author Should
Apr 05, 2025
-
Expressways Are Safer Than Other Types Of Roads Because
Apr 05, 2025
-
Miscible Liquids Such As Water And Alcohol Are Mutually
Apr 05, 2025
-
Jjs Mother Objects To A Goal His Iep Team Recommended
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Match Each Type Of Factorial Design To The Correct Definition. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
