One-half Of A Number Y Is More Than 22
Breaking News Today
Jun 05, 2025 · 5 min read
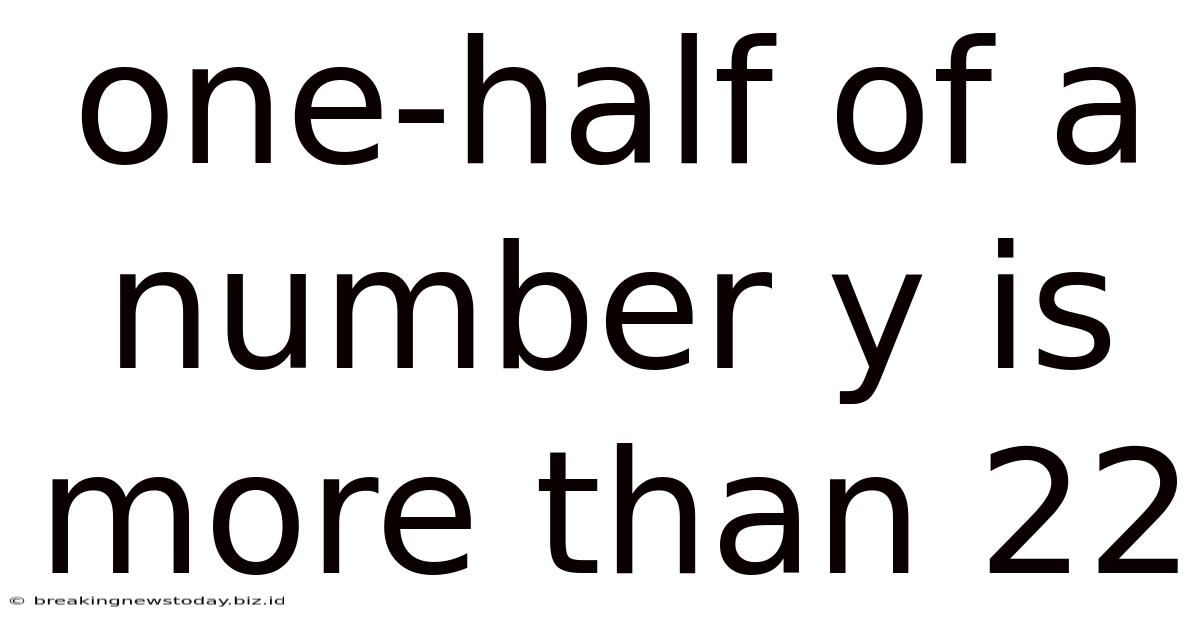
Table of Contents
One-Half of a Number Y is More Than 22: A Deep Dive into Mathematical Inequalities
This article explores the mathematical inequality "one-half of a number y is more than 22," delving into its solution, practical applications, and extensions to more complex scenarios. We'll examine different approaches to solving this inequality, discuss its graphical representation, and illustrate its relevance in real-world problems. Understanding this seemingly simple inequality provides a foundation for tackling more challenging mathematical concepts.
Understanding the Inequality: ½y > 22
The statement "one-half of a number y is more than 22" translates directly into the mathematical inequality:
½y > 22
This inequality indicates that half of an unknown number, represented by 'y', is greater than 22. Our goal is to find the range of values for 'y' that satisfy this condition.
Solving the Inequality: Isolating the Variable
To solve for 'y', we need to isolate the variable on one side of the inequality sign. We can achieve this through a series of algebraic manipulations, remembering that the rules for manipulating inequalities are slightly different than those for equations. Specifically, when multiplying or dividing both sides of an inequality by a negative number, we must reverse the direction of the inequality sign.
Here's the step-by-step solution:
-
Multiply both sides by 2: This eliminates the fraction, giving us:
y > 44
This is our solution. Any value of 'y' greater than 44 will satisfy the original inequality.
Verification: Checking the Solution
Let's test our solution with a few values:
- y = 45: ½(45) = 22.5, which is greater than 22. This confirms our solution.
- y = 44: ½(44) = 22, which is not greater than 22. This confirms the strict inequality (>).
- y = 100: ½(100) = 50, which is greater than 22. This further validates our solution.
Graphical Representation: Visualizing the Solution
The solution, y > 44, can be visually represented on a number line. We would draw a number line, mark the point 44, and shade the region to the right of 44. An open circle at 44 indicates that 44 itself is not included in the solution set.
This graphical representation provides a clear and intuitive understanding of the range of values that satisfy the inequality.
Real-World Applications: Where Inequalities Matter
Inequalities like this one are not just abstract mathematical concepts; they have numerous practical applications in various fields:
1. Business and Finance: Profit Margins and Targets
Imagine a business setting a target profit margin. If a company wants its profit (y) to be more than double its initial investment (22), the inequality would be represented as:
½y > 22
Solving this reveals that the profit needs to be greater than 44 to meet the target. This scenario illustrates the use of inequalities in setting and evaluating financial goals.
2. Engineering and Physics: Safety Margins and Load Limits
In engineering, safety factors are crucial. Consider a bridge designed to support a maximum load of 44 tons. To ensure a safety margin, engineers might require the load-bearing capacity (y) to be more than double the maximum expected load:
½y > 44
This means the bridge must support more than 88 tons to guarantee a sufficient safety factor. Inequalities play a critical role in ensuring structural integrity and safety.
3. Everyday Life: Budgeting and Savings
Suppose someone wants to save more than half of their monthly income (y) to achieve a specific financial goal, say, saving more than $22. The inequality would be:
½y > 22
Solving for y shows that they need to earn more than $44 per month to meet their savings target. This example demonstrates the relevance of inequalities in personal finance management.
Extending the Concept: More Complex Inequalities
While the initial inequality was straightforward, let's explore some more complex scenarios involving the same fundamental concept:
1. Compound Inequalities: Combining Multiple Conditions
Consider a scenario where the profit (y) must be more than double the initial investment (22) and less than five times the investment:
½y > 22 and y < 110
Solving both inequalities independently and then finding the intersection of their solution sets would provide the range of values for 'y' satisfying both conditions.
2. Inequalities with Multiple Variables: Introducing Additional Factors
Let's introduce another variable, 'x', representing expenses. Suppose the profit (y) needs to be more than double the initial investment (22) plus the expenses (x):
½y > 22 + x
To solve this, we would need additional information about the value of 'x' or express 'y' in terms of 'x'. This exemplifies how inequalities can handle multiple variables reflecting real-world complexities.
3. Inequalities with Absolute Values: Handling Distances
Absolute values introduce a different layer of complexity. Consider the inequality:
|½y| > 22
This implies that the absolute value of half of 'y' is greater than 22. This means that ½y > 22 or ½y < -22. Solving each inequality separately yields two distinct solution sets that must be combined.
Conclusion: The Power of Inequalities in Problem Solving
The simple inequality, "one-half of a number y is more than 22," while seemingly basic, provides a powerful entry point into the world of mathematical inequalities. By understanding how to solve and interpret inequalities, we gain valuable tools for modeling and solving real-world problems across various disciplines. From managing personal finances to ensuring structural integrity, the applications are vast and far-reaching. Mastering this fundamental concept sets the stage for tackling more complex inequalities and furthering our understanding of mathematical relationships. The ability to translate word problems into mathematical expressions and then solve them effectively is a key skill applicable throughout many areas of life. This seemingly simple inequality is a stepping stone to a deeper understanding of advanced mathematical concepts, highlighting the interconnectedness of mathematics and real-world challenges. The power of inequalities lies not only in their mathematical solution but also in their capacity to represent and solve a wide range of practical problems, making them an essential tool in various fields.
Latest Posts
Latest Posts
-
Which Situation Is Most Likely To Cause Peer Conflict
Jun 06, 2025
-
4 01 Quiz Independent Dependent And Noun Clauses
Jun 06, 2025
-
0 8 Is 10 Times As Great As Which Decimal
Jun 06, 2025
-
What Person Does Jake Ask To Help Find The Museum
Jun 06, 2025
-
If Lmn Xyz Which Congruences Are True By Cpctc
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about One-half Of A Number Y Is More Than 22 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.