One Hundredth More Than 2.75 Is
Breaking News Today
Jun 07, 2025 · 5 min read
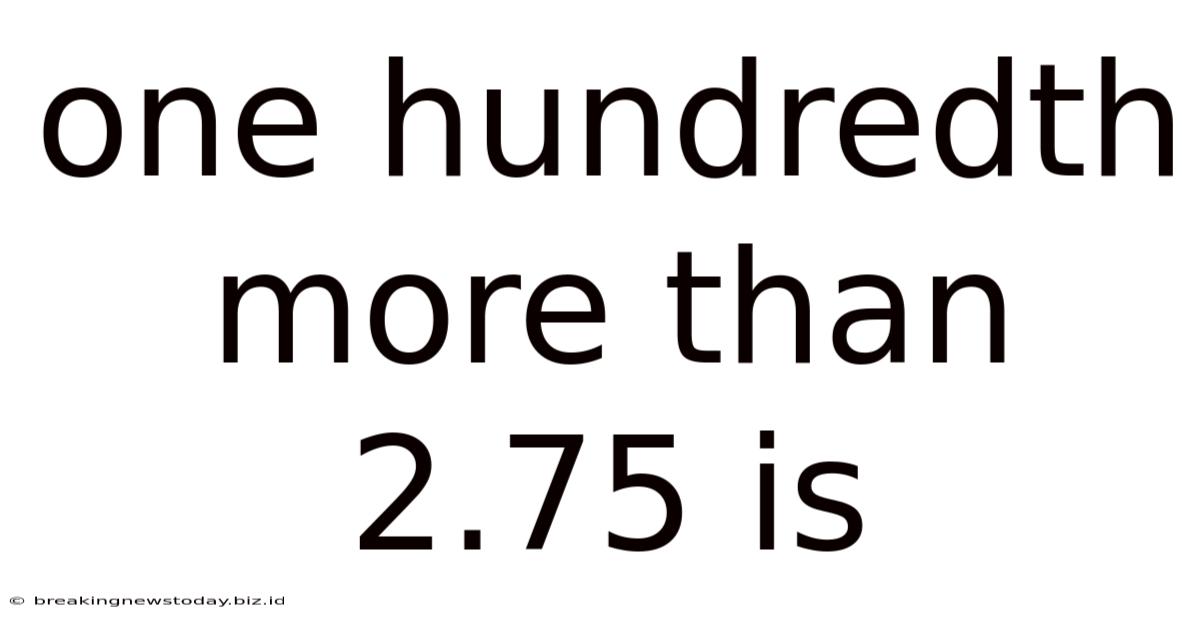
Table of Contents
One Hundredth More Than 2.75 Is: A Deep Dive into Decimal Arithmetic and its Applications
This seemingly simple question, "One hundredth more than 2.75 is?", opens the door to a fascinating exploration of decimal arithmetic, its practical applications, and the underlying mathematical principles. While the answer itself is straightforward, understanding the process and its context unlocks a broader appreciation for numerical operations and their relevance in various fields.
Understanding Decimal Numbers
Before we tackle the problem directly, let's solidify our understanding of decimal numbers. Decimals represent fractions where the denominator is a power of 10 (10, 100, 1000, and so on). The decimal point separates the whole number part from the fractional part. For instance, in the number 2.75, '2' represents the whole number, while '.75' represents the fractional part, which can also be expressed as 75/100 or ¾.
Place Value in Decimals
The place value system is crucial for understanding decimal operations. Each digit to the right of the decimal point represents a decreasing power of 10:
- Tenths (1/10): The first digit after the decimal point.
- Hundredths (1/100): The second digit after the decimal point.
- Thousandths (1/1000): The third digit after the decimal point, and so on.
In 2.75, the '7' is in the tenths place (representing 7/10), and the '5' is in the hundredths place (representing 5/100).
Calculating One Hundredth More Than 2.75
Now, let's address the core question: what is one hundredth more than 2.75? "One hundredth" is equivalent to 0.01. Therefore, we need to add 0.01 to 2.75:
2.75 + 0.01 = 2.76
Therefore, one hundredth more than 2.75 is 2.76.
Practical Applications of Decimal Arithmetic
The seemingly simple operation of adding one hundredth to a number has far-reaching applications across various disciplines:
1. Finance and Accounting
Decimal arithmetic is fundamental to financial calculations. Interest rates, stock prices, currency exchange rates, and many other financial metrics are expressed as decimals. Understanding decimal addition, subtraction, multiplication, and division is crucial for accurate financial reporting, investment analysis, and personal budgeting. For example, calculating compound interest requires repeated decimal addition. Similarly, understanding changes in stock prices, expressed as decimal fractions, is vital for investors.
2. Measurement and Engineering
Many physical measurements, such as length, weight, volume, and temperature, often involve decimal values. Engineers and scientists frequently utilize decimals in their calculations, ensuring precision in design, construction, and manufacturing processes. For instance, in engineering drawings, dimensions are often specified down to hundredths or even thousandths of an inch or millimeter, requiring precise decimal calculations for accurate construction.
3. Science and Data Analysis
Scientific experiments often generate data containing decimal numbers. Analyzing this data frequently involves adding, subtracting, averaging, and performing other calculations using decimals. This is vital for drawing accurate conclusions from experimental results. For instance, in chemistry, concentrations of solutions are often expressed as decimals, and calculations involving these concentrations require precise decimal arithmetic. Similarly, in physics, many physical quantities are measured in decimal values, requiring careful handling of decimal numbers.
4. Computing and Programming
Computers use binary systems (base-2) internally, but they can easily represent and manipulate decimal numbers. Programming languages handle decimal arithmetic seamlessly, allowing developers to create applications for diverse fields, ranging from financial modelling to scientific simulations. Accuracy in decimal arithmetic is crucial for reliable software functioning, particularly in programs related to finance, simulations, and scientific calculations.
5. Everyday Life
Beyond specialized fields, decimal arithmetic is used in our everyday lives:
- Shopping: Calculating the total cost of items, including sales tax.
- Cooking: Measuring ingredients precisely, using decimals in recipes.
- Travel: Understanding distances and fuel consumption, expressed in decimal values.
Expanding the Understanding: Further Exploration of Decimals
This simple problem of adding one hundredth to 2.75 opens avenues for more complex calculations and concepts:
1. Percentage Increases and Decreases
Understanding the addition of one hundredth is directly related to percentage changes. Adding 0.01 to 2.75 represents a 1% increase. Similarly, subtracting 0.01 would represent a 1% decrease. This concept is widely used in finance, economics, and statistics.
2. Scientific Notation
For extremely large or small numbers, scientific notation (using powers of 10) becomes essential. It simplifies the representation and manipulation of such numbers. Understanding decimals is crucial for working with scientific notation, as decimals are frequently used to express the mantissa (the numerical part) of a number in scientific notation.
3. Significant Figures and Rounding
In scientific and engineering contexts, the concept of significant figures is paramount. Significant figures determine the precision of a measurement or calculation. Rounding numbers to a specific number of significant figures is a common practice that often involves working with decimals.
4. Decimal to Fraction Conversions
The ability to convert decimals to fractions and vice versa enhances our understanding of their relationship. For example, 2.75 can be expressed as the fraction 11/4. This conversion facilitates calculations and problem-solving in specific scenarios.
5. Advanced Mathematical Operations
Decimals are fundamental for more advanced mathematical operations, including calculus, where infinitesimal changes are often expressed using decimals.
Conclusion
The seemingly simple question, "One hundredth more than 2.75 is?", reveals the profound importance and widespread application of decimal arithmetic. From simple everyday calculations to complex scientific computations, decimals are an integral part of our numerical world. Mastering decimal operations strengthens numerical literacy, enhancing our ability to engage with various fields and solve problems effectively. Understanding the principles behind decimal operations, including place value, significant figures, and conversions, builds a solid foundation for tackling more advanced mathematical concepts and real-world applications. The ability to perform these basic calculations accurately and efficiently is a skill that is invaluable across a multitude of disciplines and everyday life situations.
Latest Posts
Latest Posts
-
Show One Way To Count From 82 To 512
Jun 07, 2025
-
On What Did The Carolingian Renaissance Greatly Depend
Jun 07, 2025
-
Which Of The Following Is A Key Desired Telework Skill
Jun 07, 2025
-
Choose The Correct Translation Of The Following Time 3 10
Jun 07, 2025
-
Which Processes Relate To Mechanical Weathering Check All That Apply
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about One Hundredth More Than 2.75 Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.