Round This Number To The Nearest One. 87.6
Breaking News Today
Jun 06, 2025 · 5 min read
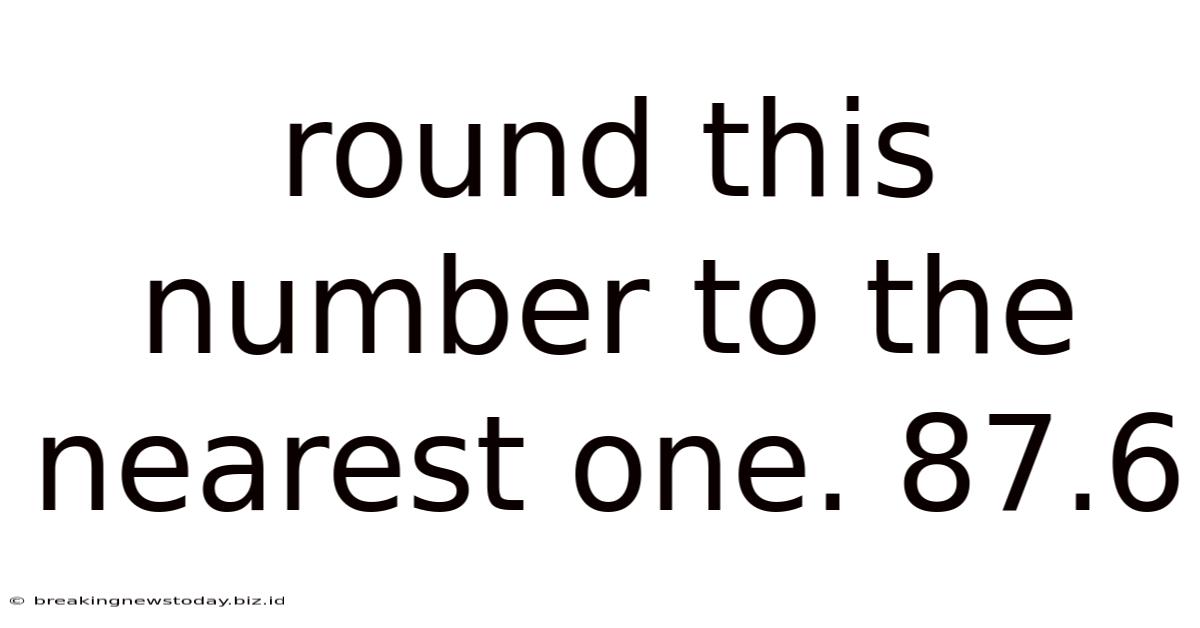
Table of Contents
Rounding Numbers: A Comprehensive Guide with Focus on 87.6
Rounding numbers is a fundamental mathematical concept with far-reaching applications across various fields. From everyday calculations to complex scientific computations, understanding how to round numbers correctly ensures accuracy and efficiency. This article delves deep into the process of rounding, focusing specifically on rounding the number 87.6 to the nearest one, and expanding upon the broader principles and practical uses of rounding.
Understanding the Concept of Rounding
Rounding involves approximating a number to a certain level of precision. Instead of using the exact value, we simplify it by reducing the number of significant digits. This is particularly useful when dealing with:
- Decimal numbers: Numbers with digits after the decimal point. Rounding allows for easier handling and interpretation of these numbers.
- Large numbers: Simplifying large numbers improves readability and makes calculations less cumbersome.
- Estimates and approximations: In scenarios where precise values aren't required, rounding offers a quick and practical way to obtain an approximate result.
The process of rounding relies on identifying the place value to which you're rounding and examining the digit immediately to its right. This digit determines whether we round up or down.
Rounding 87.6 to the Nearest One
Let's focus on the specific example of rounding 87.6 to the nearest one. The "one" refers to the ones place, which is the digit in the units position.
- Identify the ones digit: In 87.6, the ones digit is 7.
- Examine the digit to its right: The digit immediately to the right of the ones digit is 6.
- Apply the rounding rule: The standard rounding rule is:
- If the digit to the right is 5 or greater, round the ones digit up.
- If the digit to the right is less than 5, keep the ones digit as it is.
- Round up: Since the digit to the right of 7 (which is 6) is greater than or equal to 5, we round the 7 up to 8.
- Result: Therefore, 87.6 rounded to the nearest one is 88.
Different Rounding Methods
While the standard rounding method (as illustrated above) is commonly used, there are other variations, each with its own set of rules and applications. These include:
1. Rounding Down (Floor Function)
Rounding down always involves selecting the nearest smaller integer. Regardless of the digit to the right of the ones place, the number is always rounded down. For example, rounding 87.6 down would result in 87. This method is frequently used in situations where underestimation is preferred over overestimation, such as in inventory management or resource allocation.
2. Rounding Up (Ceiling Function)
Rounding up always involves selecting the nearest larger integer. Regardless of the digit to the right of the ones place, the number is always rounded up. Rounding 87.6 up would result in 88. This is often used in scenarios where overestimation is safer than underestimation, such as in estimating project costs or time.
3. Rounding to Significant Figures
This method focuses on the number of significant digits a number should have after rounding. The number of significant figures determines the accuracy level required. For instance, if we need to round 87.6 to two significant figures, the result would still be 88. However, if we needed only one significant figure, it would be rounded to 90. This approach is crucial in scientific and engineering applications where precision is critical.
4. Rounding to Even (Banker's Rounding)
Banker's rounding is a variation designed to reduce bias in repeated rounding. When the digit to the right is exactly 5, it rounds to the nearest even number. For example, 87.5 would round to 88 (an even number), while 86.5 would round to 86. This method helps to minimize cumulative errors over many rounding operations.
Practical Applications of Rounding
Rounding is not merely a mathematical exercise; it finds practical use in various real-world scenarios:
- Finance: Rounding is vital in financial transactions. Amounts are often rounded to the nearest cent or dollar for ease of accounting and reporting.
- Engineering: In engineering design and construction, rounding is used to simplify measurements and calculations, ensuring practicality and feasibility.
- Science: Rounding is essential in scientific data analysis to manage significant figures and present results with appropriate accuracy.
- Statistics: Rounding is used extensively in statistical analysis to represent data concisely and prevent unnecessary detail.
- Everyday Life: We round numbers constantly in our daily lives, for instance, when estimating distances, quantities, or costs.
Errors Introduced by Rounding
While rounding simplifies calculations, it's essential to be aware of the potential for introducing rounding errors. These errors accumulate, especially when rounding numerous times in a single calculation. In critical applications, techniques for managing and minimizing rounding errors are necessary.
Choosing the Right Rounding Method
The selection of an appropriate rounding method depends on the context and the desired level of accuracy. Understanding the implications of each method ensures that the chosen approach aligns with the specific requirements of the task. For everyday estimations, the standard rounding method is often sufficient. However, in more demanding applications, such as those involving financial calculations or scientific data analysis, it may be necessary to employ more sophisticated rounding methods, like Banker's rounding or rounding to significant figures, to minimize errors and maintain accuracy.
Conclusion: Mastering Rounding Techniques
Rounding numbers is a skill that transcends simple mathematics; it's a crucial tool for effective data handling and calculation. Understanding the different rounding methods and their applications empowers individuals to navigate various situations with confidence, ensuring accuracy and efficiency in their computations, whether it's rounding 87.6 to the nearest whole number or tackling more complex rounding challenges. The ability to accurately and appropriately round numbers is a fundamental skill for anyone working with numbers in any capacity. By mastering these techniques, one can improve their mathematical proficiency and reduce the risk of errors in calculations, ultimately leading to more accurate and reliable results. Remember to always consider the context and the required level of precision when choosing your rounding method.
Latest Posts
Latest Posts
-
Which Sentence Best Contrasts Two Things
Jun 07, 2025
-
18 Is 24 Of What Number
Jun 07, 2025
-
Some Polyhedrons Are Both Prisms And Pyramids
Jun 07, 2025
-
Which Shows A Successful Communication Strategy For An Adolescent
Jun 07, 2025
-
Which Statement Best Explains Why Producers Conduct Market Research
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Round This Number To The Nearest One. 87.6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.