Sari Is Factoring The Polynomial 2x 2 5x 3
Breaking News Today
Jun 07, 2025 · 5 min read
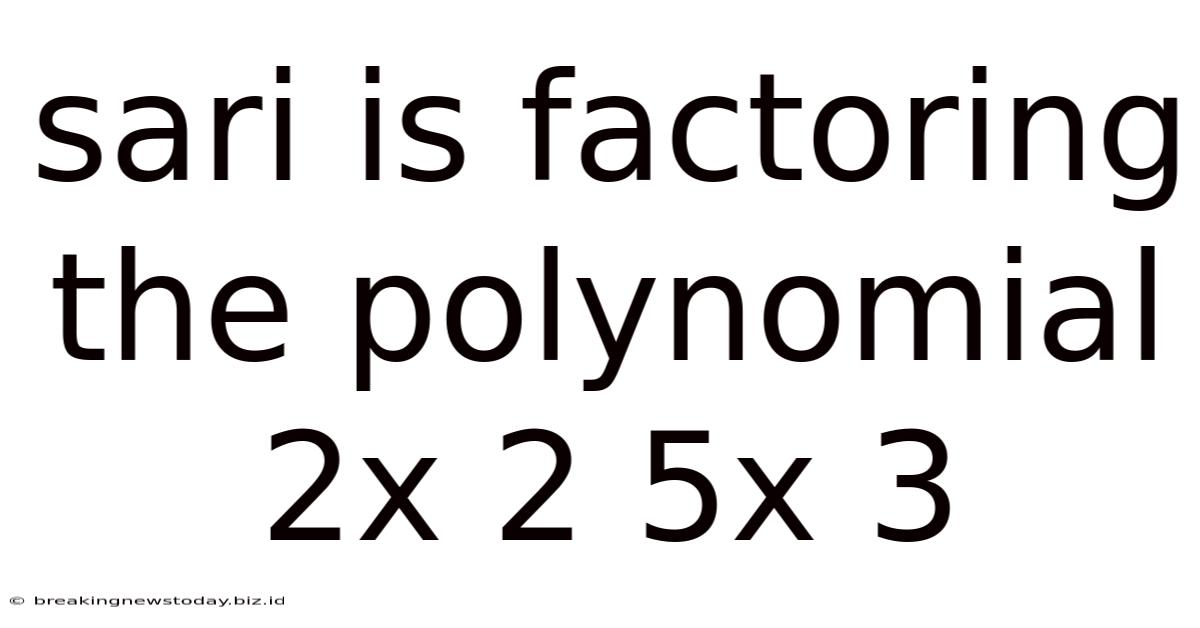
Table of Contents
Factoring Quadratics: A Deep Dive into 2x² + 5x + 3
Factoring polynomials is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding more advanced mathematical concepts. This article will delve into the process of factoring the quadratic polynomial 2x² + 5x + 3, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll move beyond simply finding the answer and explore the why behind each step, solidifying your understanding of quadratic factoring.
Understanding Quadratic Polynomials
Before we tackle the specific problem of factoring 2x² + 5x + 3, let's establish a strong foundation. A quadratic polynomial is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form:
ax² + bx + c
where a, b, and c are constants, and a ≠ 0. In our case, a = 2, b = 5, and c = 3.
Method 1: AC Method (Product-Sum Method)
This is a widely used method for factoring quadratic trinomials. The steps are as follows:
-
Find the product 'ac': In our case, a = 2 and c = 3, so ac = 2 * 3 = 6.
-
Find two numbers that add up to 'b' and multiply to 'ac': We need two numbers that add up to 5 (our b value) and multiply to 6. These numbers are 2 and 3 (2 + 3 = 5 and 2 * 3 = 6).
-
Rewrite the middle term: Rewrite the middle term (5x) as the sum of the two numbers we found, multiplied by x. This gives us: 2x² + 2x + 3x + 3
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
(2x² + 2x) + (3x + 3) = 2x(x + 1) + 3(x + 1)
-
Factor out the common binomial: Notice that both terms now share the common binomial factor (x + 1). Factor this out:
(x + 1)(2x + 3)
Therefore, the factored form of 2x² + 5x + 3 is (x + 1)(2x + 3).
Verifying the Solution
To ensure our factoring is correct, we can expand the factored form using the distributive property (FOIL method):
(x + 1)(2x + 3) = x(2x) + x(3) + 1(2x) + 1(3) = 2x² + 3x + 2x + 3 = 2x² + 5x + 3
This matches our original polynomial, confirming that our factoring is accurate.
Method 2: Trial and Error
This method involves systematically trying different combinations of binomial factors until you find the correct one. It's particularly effective when the coefficient of x² (a) is small.
-
Consider the factors of 'a' and 'c': The factors of 'a' (2) are 1 and 2. The factors of 'c' (3) are 1 and 3.
-
Set up binomial factors: We'll set up the binomial factors as ( _x + _ )( _x + _ ), where the blanks represent the factors of 'a' and 'c' we'll test.
-
Test combinations: We'll try different combinations:
- (x + 1)(2x + 3): Expanding this gives 2x² + 5x + 3 (Correct!)
- (x + 3)(2x + 1): Expanding this gives 2x² + 7x + 3 (Incorrect)
- (2x + 1)(x + 3): Expanding this gives 2x² + 7x + 3 (Incorrect)
- (2x + 3)(x + 1): Expanding this gives 2x² + 5x + 3 (Correct!)
As you can see, the trial and error method can be time-consuming, but it reinforces understanding of factor interactions. The correct combination is (x + 1)(2x + 3).
Method 3: Quadratic Formula
While not a direct factoring method, the quadratic formula can help find the roots (solutions) of the quadratic equation 2x² + 5x + 3 = 0. These roots can then be used to determine the factors.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values (a = 2, b = 5, c = 3):
x = [-5 ± √(5² - 4 * 2 * 3)] / (2 * 2) = [-5 ± √(25 - 24)] / 4 = [-5 ± 1] / 4
This gives us two solutions:
x₁ = (-5 + 1) / 4 = -1 x₂ = (-5 - 1) / 4 = -3/2
These roots correspond to the factors (x + 1) and (x + 3/2). To obtain integer coefficients, multiply the second factor by 2: (2x + 3). Thus, the factored form is (x + 1)(2x + 3).
Applications of Factoring
Factoring quadratic polynomials has numerous applications in mathematics and beyond. Some key applications include:
- Solving quadratic equations: Setting the factored polynomial equal to zero allows us to find the roots of the equation, representing the x-intercepts on a graph.
- Simplifying algebraic expressions: Factoring can simplify complex expressions, making them easier to manipulate and analyze.
- Calculus: Factoring is essential in calculus for finding derivatives and integrals.
- Physics and engineering: Quadratic equations and their solutions are used extensively in physics and engineering to model various phenomena, such as projectile motion and circuit analysis.
Advanced Factoring Techniques (Beyond the Scope of 2x² + 5x + 3)
While this article focuses on factoring 2x² + 5x + 3, it's important to note that more complex polynomials may require advanced techniques, including:
- Factoring by substitution: This involves substituting a variable to simplify the polynomial before factoring.
- Factoring sums and differences of cubes: These specialized formulas handle polynomials of the form a³ + b³ and a³ - b³.
- Factoring using the difference of squares: This applies to polynomials in the form a² - b².
Conclusion
Factoring the quadratic polynomial 2x² + 5x + 3, whether using the AC method, trial and error, or indirectly through the quadratic formula, provides a valuable exercise in understanding fundamental algebraic principles. Mastering these techniques is critical for success in higher-level mathematics and related fields. Remember to practice regularly and explore different methods to develop a strong intuition for factoring polynomials. This will not only improve your problem-solving skills but also build a solid foundation for future mathematical endeavors. By understanding the why behind each step, you'll transition from simply memorizing procedures to truly understanding the power of polynomial factorization.
Latest Posts
Latest Posts
-
Which Statement Describes A Benefit Of Desalination Technology
Jun 07, 2025
-
What Is The Narrowest Definition Of The Number 2 3
Jun 07, 2025
-
Which Statement Is True Regarding The Dimensions Of Wellness
Jun 07, 2025
-
Which Statement Best Describes The Theme Of Song Of Myself
Jun 07, 2025
-
Which Best Describes The Use Of Irony In This Excerpt
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Sari Is Factoring The Polynomial 2x 2 5x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.