Simplify The Expression X 5 X 7
Breaking News Today
Jun 03, 2025 · 4 min read
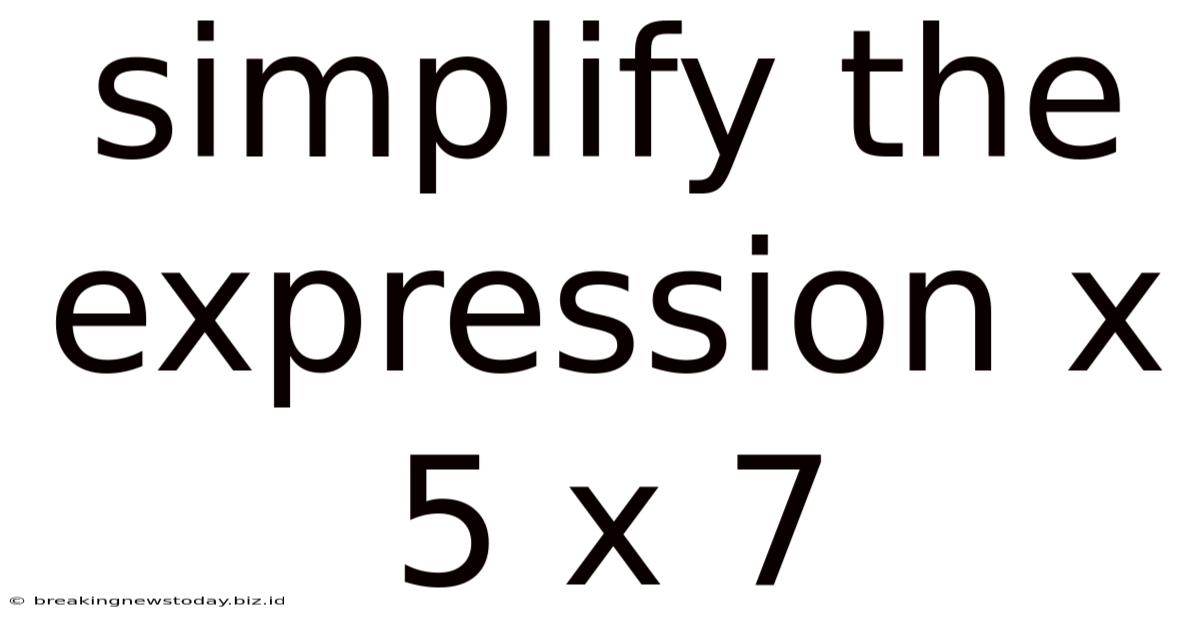
Table of Contents
Simplifying the Expression x⁵ x⁷: A Deep Dive into Algebraic Principles
This article delves into the seemingly simple mathematical expression x⁵ x⁷, exploring its simplification, the underlying algebraic principles involved, and extending the concept to more complex scenarios. We'll cover the fundamental rules of exponents, provide practical examples, and offer insights into how this foundational concept forms the basis for more advanced algebraic manipulations. This comprehensive guide is designed for students, educators, and anyone seeking a deeper understanding of algebraic simplification.
Understanding Exponents and Their Properties
Before we tackle the simplification of x⁵ x⁷, let's establish a solid foundation in exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For instance, in the expression x⁵, 'x' is the base, and '5' is the exponent, meaning x multiplied by itself five times: x * x * x * x * x.
Several crucial properties govern the manipulation of exponents. These properties are the cornerstones of simplifying expressions like x⁵ x⁷:
1. Product of Powers Property:
This property is the key to simplifying our expression. It states that when multiplying two exponential expressions with the same base, you add the exponents. Mathematically:
xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾
This rule is the direct solution to our problem. We will apply this directly in the next section.
2. Power of a Power Property:
This property deals with raising an exponential expression to another power. It states that when raising a power to a power, you multiply the exponents. Mathematically:
(xᵃ)ᵇ = x⁽ᵃ*ᵇ⁾
This property, while not directly applied to the simplification of x⁵ x⁷, is crucial in understanding more complex exponential expressions.
3. Power of a Product Property:
This property describes the effect of raising a product to a power. It states that when raising a product to a power, each factor in the product is raised to that power. Mathematically:
(xy)ᵃ = xᵃyᵃ
This property is relevant when dealing with expressions involving multiple variables raised to powers.
4. Quotient of Powers Property:
This property governs the division of exponential expressions with the same base. It states that when dividing two exponential expressions with the same base, you subtract the exponents. Mathematically:
xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾ (where x ≠ 0)
Understanding this property is essential for simplifying more complex rational expressions involving exponents.
5. Zero Exponent Property:
Any non-zero base raised to the power of zero equals 1. Mathematically:
x⁰ = 1 (where x ≠ 0)
6. Negative Exponent Property:
A base raised to a negative exponent is equivalent to the reciprocal of the base raised to the positive exponent. Mathematically:
x⁻ᵃ = 1/xᵃ (where x ≠ 0)
Simplifying x⁵ x⁷ Using the Product of Powers Property
Now, let's apply the Product of Powers Property to simplify our expression, x⁵ x⁷:
Since both terms have the same base (x), we add the exponents:
x⁵ x⁷ = x⁽⁵⁺⁷⁾ = x¹²
Therefore, the simplified form of the expression x⁵ x⁷ is x¹². This signifies that x is multiplied by itself twelve times.
Extending the Concept: More Complex Scenarios
The principles illustrated above are fundamental and can be extended to more complex scenarios. Let's explore a few examples:
Example 1: Simplify (2x³y²)⁴ (3xy⁵)².
First, we apply the power of a product property:
(2x³y²)⁴ = 2⁴(x³)^4(y²)⁴ = 16x¹²y⁸ (3xy⁵)² = 3²(x)²(y⁵)² = 9x²y¹⁰
Now, we multiply these simplified expressions, using the product of powers property for the same base variables:
16x¹²y⁸ * 9x²y¹⁰ = (16 * 9)x⁽¹²⁺²⁾y⁽⁸⁺¹⁰⁾ = 144x¹⁴y¹⁸
Example 2: Simplify (x⁵/x²)³.
First, we simplify the expression inside the parenthesis using the quotient of powers property:
x⁵/x² = x⁽⁵⁻²⁾ = x³
Now, we raise this simplified expression to the power of 3 using the power of a power property:
(x³)^3 = x⁽³*³⁾ = x⁹
Therefore, the simplified expression is x⁹.
Example 3: Simplify (2x⁻²y³)⁻¹.
We apply the power of a product property and the negative exponent property:
(2x⁻²y³)⁻¹ = 2⁻¹(x⁻²)⁻¹(y³)⁻¹ = (1/2)x²(1/y³) = x²/2y³
Practical Applications and Real-World Relevance
Understanding exponential expressions and their simplification is crucial in various fields:
-
Physics: Exponential functions are prevalent in describing phenomena like radioactive decay, population growth, and the behavior of waves.
-
Engineering: Exponential expressions are essential in calculating the strength of materials, analyzing circuits, and modeling various systems.
-
Finance: Compound interest calculations rely heavily on exponential functions.
-
Computer Science: Algorithms and data structures often involve exponential time complexity analysis.
-
Statistics: Exponential distributions are frequently used to model various data sets.
-
Economics: Growth models and decay processes are often represented using exponential functions.
Conclusion: Mastering the Fundamentals
The simplification of x⁵ x⁷, although seemingly straightforward, provides a robust foundation for understanding and mastering more complex algebraic manipulations. By grasping the fundamental properties of exponents, we can confidently tackle increasingly challenging expressions. Remember, consistent practice and a thorough understanding of these rules are key to achieving proficiency in algebra and its numerous applications. The ability to simplify complex expressions improves problem-solving skills across multiple disciplines, highlighting the importance of mastering these seemingly simple algebraic principles. Further exploration of these concepts will unlock more advanced mathematical tools and expand your analytical abilities significantly.
Latest Posts
Latest Posts
-
1 1 10 Practice Written Assignment Spanish 2
Jun 05, 2025
-
Find The Length X To The Nearest Whole Number
Jun 05, 2025
-
What Expression Represents The Measure Of Angle X
Jun 05, 2025
-
Which Statement Best Describes The Green Knights Chivalric Values
Jun 05, 2025
-
Which Table Of Values Corresponds To The Graph Below
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Expression X 5 X 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.