Solve Each Of The Quadratic Equations 3x 0.5 X2
Breaking News Today
Jun 08, 2025 · 5 min read
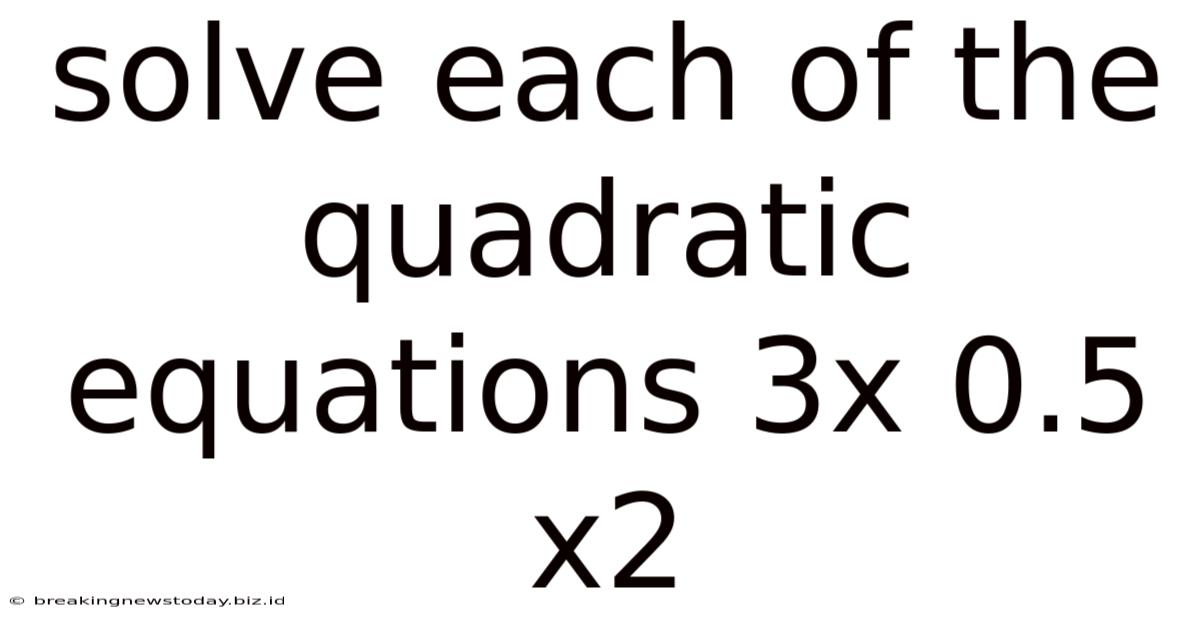
Table of Contents
Solving the Quadratic Equation: 3x - 0.5x² = 0
This article will delve into the comprehensive solution of the quadratic equation 3x - 0.5x² = 0, exploring various methods and providing a detailed understanding of the underlying mathematical principles. We'll cover the standard approaches, discuss the significance of the solutions, and offer insights into how to tackle similar quadratic equations effectively.
Understanding Quadratic Equations
Before we jump into solving our specific equation, let's establish a foundational understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (typically 'x') is 2. The general form of a quadratic equation is:
ax² + bx + c = 0
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero (otherwise it wouldn't be a quadratic equation). The solutions to a quadratic equation are also known as its roots or zeros. These represent the x-values where the quadratic function intersects the x-axis (i.e., where y=0).
Methods for Solving Quadratic Equations
Several methods exist for solving quadratic equations. The most common include:
- Factoring: This method involves expressing the quadratic equation as a product of two linear expressions. It's the simplest method, but it only works for easily factorable equations.
- Quadratic Formula: This formula provides a direct solution for any quadratic equation, regardless of its factorability. It's a reliable and universally applicable method.
- Completing the Square: This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. It's a valuable technique for understanding the structure of quadratic equations and can be useful in certain contexts.
- Graphing: This method involves plotting the quadratic function and visually identifying the x-intercepts, which represent the solutions. While visually intuitive, it's less precise than algebraic methods.
Solving 3x - 0.5x² = 0 Using Factoring
Our specific equation, 3x - 0.5x² = 0, is particularly amenable to the factoring method. First, let's rearrange the equation to conform to the standard form:
-0.5x² + 3x = 0
Now, we can factor out the common factor of 'x':
x(-0.5x + 3) = 0
This equation is now in factored form. The product of two terms is zero if and only if at least one of the terms is zero. Therefore, we have two possible solutions:
- x = 0
- -0.5x + 3 = 0
Solving the second equation for x:
-0.5x = -3 x = -3 / -0.5 x = 6
Therefore, the solutions to the quadratic equation 3x - 0.5x² = 0 are x = 0 and x = 6.
Solving 3x - 0.5x² = 0 Using the Quadratic Formula
The quadratic formula provides a general solution for any quadratic equation of the form ax² + bx + c = 0:
x = (-b ± √(b² - 4ac)) / 2a
In our equation, 3x - 0.5x² = 0, we have a = -0.5, b = 3, and c = 0. Substituting these values into the quadratic formula:
x = (-3 ± √(3² - 4(-0.5)(0))) / 2(-0.5) x = (-3 ± √9) / -1 x = (-3 ± 3) / -1
This gives us two solutions:
- x = (-3 + 3) / -1 = 0 / -1 = 0
- x = (-3 - 3) / -1 = -6 / -1 = 6
As expected, we obtain the same solutions as with the factoring method.
Solving 3x - 0.5x² = 0 Using Completing the Square
While less straightforward for this particular equation, let's demonstrate the completing the square method. First, we rearrange the equation:
-0.5x² + 3x = 0
Multiplying by -2 to eliminate the fraction:
x² - 6x = 0
Now, we complete the square. To do this, we take half of the coefficient of the x term (-6), square it ((-3)² = 9), and add it to both sides of the equation:
x² - 6x + 9 = 9
The left side is now a perfect square trinomial:
(x - 3)² = 9
Taking the square root of both sides:
x - 3 = ±3
Solving for x:
- x - 3 = 3 => x = 6
- x - 3 = -3 => x = 0
Again, we arrive at the same solutions.
Graphical Representation and Interpretation
The solutions x = 0 and x = 6 represent the x-intercepts of the parabola defined by the quadratic function y = -0.5x² + 3x. Graphically, this means the parabola intersects the x-axis at these two points. This visual representation provides a clear understanding of the equation's solutions within the context of the function's behavior. The parabola opens downwards because the coefficient of the x² term is negative.
Significance of the Solutions
The solutions x = 0 and x = 6 are the values of x that satisfy the equation 3x - 0.5x² = 0. In a real-world application, these solutions could represent specific points or values within a model or system described by the quadratic function. For instance, it could represent break-even points, maximum heights in projectile motion, or points where a curve intersects the x-axis. The context of the problem determines the interpretation of these solutions.
Solving Similar Quadratic Equations
The techniques demonstrated here—factoring, the quadratic formula, and completing the square—are applicable to a wide range of quadratic equations. When faced with a new quadratic equation, consider the following:
- Check for easy factoring: If the equation can be easily factored, this is often the quickest and most efficient method.
- Use the quadratic formula for a guaranteed solution: This method works for all quadratic equations, even those that are difficult or impossible to factor.
- Consider completing the square for specific situations: Completing the square can be helpful when dealing with equations in a particular form or when you need to manipulate the equation to a specific format.
Advanced Considerations: Discriminant and Nature of Roots
The discriminant, which is the expression b² - 4ac within the quadratic formula, provides valuable information about the nature of the roots:
- b² - 4ac > 0: Two distinct real roots (as in our example).
- b² - 4ac = 0: One real root (repeated root).
- b² - 4ac < 0: Two complex roots (involving imaginary numbers).
Conclusion
This comprehensive exploration of solving the quadratic equation 3x - 0.5x² = 0 demonstrates the various methods available and highlights the importance of understanding the underlying principles. Whether using factoring, the quadratic formula, completing the square, or a graphical approach, the solutions remain consistent: x = 0 and x = 6. Mastering these techniques empowers you to tackle a wide range of quadratic equations and apply this essential mathematical skill to diverse applications. Remember to always choose the method that best suits the specific equation and your understanding of the concepts involved. Understanding the nature of roots using the discriminant further enhances your ability to solve and interpret quadratic equations effectively.
Latest Posts
Latest Posts
-
Which Of The Following Best Describes The Rondo Form
Jun 08, 2025
-
How Is The Conflict Between The Twins Resolved
Jun 08, 2025
-
It Was Time For Oli To Marry
Jun 08, 2025
-
Economists Pay Close Attention To The Unemployment Rate Because
Jun 08, 2025
-
Before Being Painted A Concrete Play Area
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Solve Each Of The Quadratic Equations 3x 0.5 X2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.