Solve For A 4 A 3 12 4a
Breaking News Today
Jun 04, 2025 · 5 min read
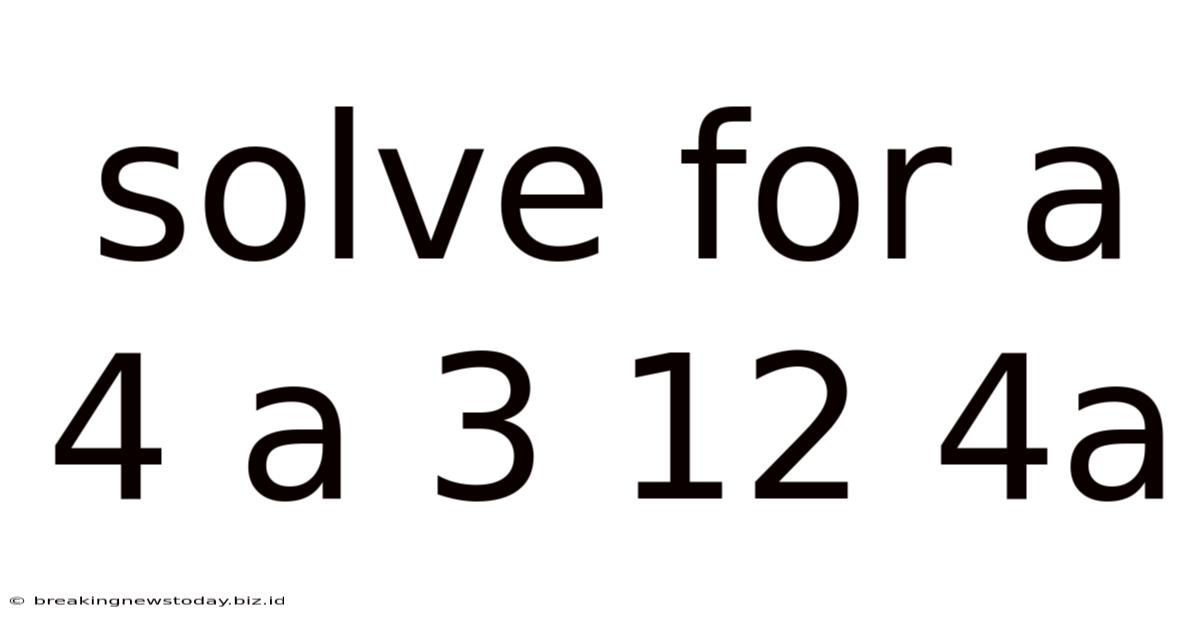
Table of Contents
Solving the Equation: 4a³ + 12 = 4a
This article delves into the solution of the cubic equation 4a³ + 12 = 4a, exploring various methods to find its roots. We'll cover the process step-by-step, focusing on algebraic manipulation, and discuss the importance of understanding different solution approaches in mathematics. We will also touch upon the practical applications of solving cubic equations in various fields.
Understanding the Equation: 4a³ + 12 = 4a
Before diving into the solution, let's analyze the given equation: 4a³ + 12 = 4a. This is a cubic equation because the highest power of the variable 'a' is 3. Solving a cubic equation means finding the values of 'a' that make the equation true. Unlike quadratic equations, which always have two solutions (real or complex), cubic equations always have at least one real solution, and potentially up to three real solutions.
Rearranging the Equation
The first step in solving any equation is to rearrange it into a standard form. In this case, we want to set the equation equal to zero. To achieve this, we subtract 4a from both sides:
4a³ - 4a + 12 = 0
This simplified form is much easier to work with. Notice that all the coefficients are divisible by 4. This allows us to further simplify the equation by dividing the entire equation by 4:
a³ - a + 3 = 0
This is the standard form of our cubic equation. This simplification makes the subsequent calculations less cumbersome.
Methods for Solving Cubic Equations
Several methods exist for solving cubic equations. The most common and often the most practical methods include:
-
Factoring: This involves expressing the cubic polynomial as a product of linear and/or quadratic factors. However, factoring is not always straightforward, and it's not always possible to factor a cubic equation easily.
-
Rational Root Theorem: The Rational Root Theorem helps identify potential rational roots (roots that are rational numbers). This theorem can significantly reduce the number of possible solutions we need to test.
-
Numerical Methods: For cubic equations that are difficult or impossible to solve algebraically, numerical methods such as the Newton-Raphson method provide approximate solutions. These methods are particularly useful when dealing with complex or irrational roots.
-
Cardano's Method (Cubic Formula): This method provides a general formula for solving cubic equations, similar to the quadratic formula. However, Cardano's method can be quite complex and often leads to cumbersome calculations.
Applying the Rational Root Theorem
Let's try using the Rational Root Theorem. The theorem states that any rational root of the polynomial equation a³ - a + 3 = 0 will be of the form p/q, where 'p' is a factor of the constant term (3 in this case) and 'q' is a factor of the leading coefficient (1 in this case).
Therefore, the possible rational roots are ±1 and ±3. Let's test these values:
- If a = 1: 1³ - 1 + 3 = 3 ≠ 0
- If a = -1: (-1)³ - (-1) + 3 = 3 ≠ 0
- If a = 3: 3³ - 3 + 3 = 27 ≠ 0
- If a = -3: (-3)³ - (-3) + 3 = -27 + 3 + 3 = -21 ≠ 0
None of the potential rational roots satisfy the equation. This suggests that the equation has no rational roots.
Numerical Methods: Approximating the Solution
Since the Rational Root Theorem didn't yield a solution, we can resort to numerical methods to approximate the real root. The Newton-Raphson method is a popular choice for its efficiency. This iterative method refines an initial guess to get closer and closer to the actual root.
The Newton-Raphson formula is:
xₙ₊₁ = xₙ - f(xₙ) / f'(xₙ)
where:
- xₙ is the current approximation
- xₙ₊₁ is the next approximation
- f(xₙ) is the value of the function at xₙ
- f'(xₙ) is the derivative of the function at xₙ
For our equation, f(a) = a³ - a + 3 and f'(a) = 3a² - 1. We need an initial guess for 'a'. Let's start with a = -1.5.
Applying the Newton-Raphson method iteratively (using a calculator or software), we can obtain a progressively better approximation of the root. After several iterations, we'll find that the real root is approximately a ≈ -1.6717.
Analyzing the Nature of Roots
Cubic equations can have three real roots, one real root and two complex roots, or three real roots where some may be repeated. Since we found one real root using the numerical method, let's explore the possibility of other real roots. Graphing the function f(a) = a³ - a + 3 can help visualize the roots. The graph will reveal if there are other points where the curve intersects the x-axis (i.e., where f(a) = 0).
By observing the graph, or using more advanced numerical methods, we can confirm that there are no other real roots. The other two roots are complex conjugates.
Practical Applications of Solving Cubic Equations
Solving cubic equations isn't just an academic exercise; it has significant applications in various fields:
-
Engineering: Cubic equations arise in various engineering problems, including structural analysis, fluid dynamics, and electrical circuit design. Determining the stability of structures, the flow of liquids, and the behavior of electrical circuits often requires solving cubic equations.
-
Physics: Cubic equations appear in physics problems related to projectile motion, oscillations, and wave mechanics. Solving these equations is crucial for understanding and predicting physical phenomena.
-
Chemistry: In chemistry, cubic equations are used in equilibrium calculations, reaction kinetics, and thermodynamics. Determining the concentrations of reactants and products often involves solving cubic equations.
-
Economics: Cubic equations can model economic phenomena such as supply and demand curves, cost functions, and production functions. Solving these equations helps analyze economic behaviors and make predictions.
Conclusion: A Multifaceted Problem
Solving the cubic equation 4a³ + 12 = 4a, or its simplified form a³ - a + 3 = 0, demonstrates the importance of understanding various mathematical techniques. While factoring might not always be feasible, the Rational Root Theorem provides a systematic approach to identify potential rational roots. However, for equations without rational roots, numerical methods, such as the Newton-Raphson method, offer accurate approximations. Remember that cubic equations can have complex roots, emphasizing the need for a comprehensive approach to find all possible solutions. The practical applications of solving cubic equations highlight their significance beyond theoretical mathematics, underscoring their role in diverse scientific and engineering disciplines. Mastering these techniques is essential for anyone working in fields that require solving polynomial equations.
Latest Posts
Latest Posts
-
What Is 0 465 Converted To A Percentage
Jun 06, 2025
-
Sandwich Makers Should Sanitize Their Work Area Every
Jun 06, 2025
-
Which Statements Are True Based On The Diagram
Jun 06, 2025
-
Ethical Exchanges Between Sellers And Buyers Should Result In
Jun 06, 2025
-
Which Is True Of Nursing Assistants And Catheters
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Solve For A 4 A 3 12 4a . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.