Solve For The Variable In 7 28 25 X
Breaking News Today
Jun 03, 2025 · 5 min read
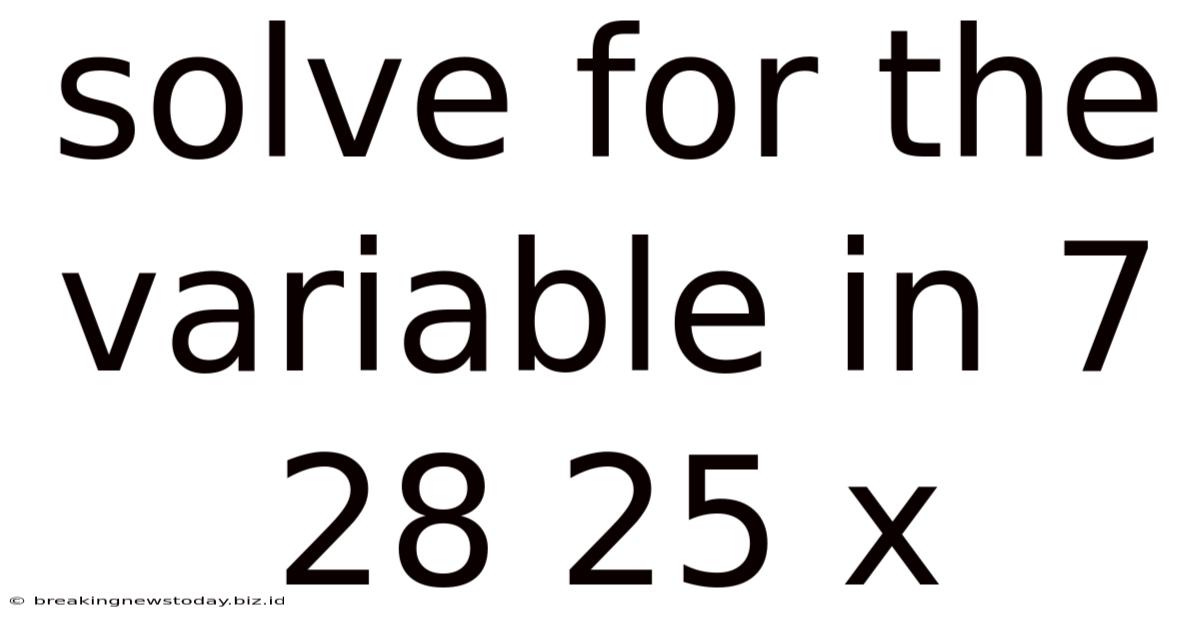
Table of Contents
Solving for the Variable: Unlocking the Mystery of 7, 28, 25, x
The seemingly simple sequence 7, 28, 25, x presents a captivating mathematical puzzle. At first glance, the connection between these numbers might seem elusive. However, by employing logical reasoning and exploring various mathematical operations, we can uncover the pattern and successfully solve for the variable 'x'. This article will delve into the process, exploring multiple approaches and highlighting the importance of pattern recognition and critical thinking in problem-solving.
Understanding the Problem: Deciphering the Pattern
Before we jump into complex calculations, let's take a step back and analyze the given sequence: 7, 28, 25. Our goal is to identify a consistent mathematical relationship between these numbers that can be extrapolated to determine the value of x. This involves considering various mathematical operations like addition, subtraction, multiplication, division, and even more complex operations.
The immediate challenge is the lack of an obvious, singular pattern. This requires a systematic approach, exploring different possibilities until a consistent relationship emerges.
Potential Approaches: Exploring Mathematical Relationships
Let's explore some potential avenues to unravel the sequence's hidden pattern:
-
Addition/Subtraction: We can examine the differences between consecutive numbers. The difference between 28 and 7 is 21 (28 - 7 = 21), and the difference between 25 and 28 is -3 (25 - 28 = -3). This doesn't immediately reveal a clear, consistent pattern.
-
Multiplication/Division: Let's investigate if there's a multiplicative relationship. 28 is four times 7 (28 = 7 * 4). However, 25 isn't directly related to 28 through a simple multiplication or division.
-
Combinations of Operations: Since a single operation doesn't reveal a straightforward pattern, we need to explore more complex combinations. Perhaps the pattern involves a combination of multiplication and subtraction, or other operations.
-
Hidden Sequences: It's possible that the sequence isn't based on a simple arithmetic pattern but rather on a more intricate relationship, perhaps involving prime numbers, Fibonacci numbers, or other mathematical sequences.
Solving the Puzzle: A Systematic Approach
To systematically solve this puzzle, let's consider various scenarios and test different mathematical operations:
Scenario 1: Focusing on the First Two Numbers
Let's focus on the relationship between 7 and 28. As mentioned earlier, 28 = 7 * 4. This suggests a multiplication factor of 4 might play a role. If we apply this to the next number, we would expect 25 to be related to 28 by a factor or operation involving 4. However, there isn't an immediately obvious direct mathematical relationship. This doesn't invalidate this approach entirely; it simply suggests further investigation is needed. Perhaps a combination with addition or subtraction is required.
Scenario 2: Considering Differences and Patterns
Let's analyze the differences between consecutive numbers again:
- 28 - 7 = 21
- 25 - 28 = -3
While these differences aren't immediately consistent, let's look for patterns within these differences themselves. The difference between these differences is: -3 - 21 = -24. This suggests the potential for a secondary pattern related to multiples of 3 or 24.
Scenario 3: Exploring Non-Linear Relationships
It's possible that the pattern isn't linear. Nonlinear relationships in mathematics often involve exponents, logarithms, or other non-linear functions. Let's explore a few possibilities. For instance, could the sequence involve squaring or cubing the numbers?
Important Note: Without further information or context, it's impossible to definitively solve for 'x' with complete certainty. The problem might be deliberately ambiguous, designed to highlight the limitations of deductive reasoning when faced with incomplete data.
The Importance of Context and Additional Information
The difficulty in solving for 'x' underscores the critical role of context in mathematical problem-solving. The sequence 7, 28, 25, x, without further information, can lead to multiple possible solutions, each valid within its own framework.
For instance:
-
If the sequence is part of a larger, more extensive data set, the overall pattern within that larger context might offer crucial clues.
-
If additional mathematical constraints or rules are given, this would dramatically narrow down the possible solutions.
-
If the problem's origin is known (e.g., a specific mathematical context or a real-world scenario), this added information might provide essential hints.
Expanding the Problem-Solving Techniques
The analysis above highlights the importance of various approaches to problem-solving. These include:
-
Systematic trial and error: This involves testing multiple possibilities until a consistent pattern emerges. Careful record-keeping of your attempts is crucial for this approach.
-
Pattern recognition: The ability to identify patterns, even subtle ones, is essential in mathematical problem-solving.
-
Logical reasoning: This involves using logical deductions to eliminate improbable solutions and focus on more plausible ones.
-
Flexibility in approach: Don't be afraid to explore different mathematical operations and techniques. A solution might involve a combination of several approaches.
-
Contextual awareness: Always consider the context of the problem. Additional information might significantly alter the problem-solving strategy.
Conclusion: The Value of Persistence and Exploration
Solving for the variable in the sequence 7, 28, 25, x showcases the challenges and rewards of mathematical problem-solving. While a definitive solution without additional context remains elusive, the exploration process itself is invaluable. It highlights the importance of critical thinking, pattern recognition, and a systematic approach. Persistence and a willingness to explore multiple avenues are key to unlocking the mysteries hidden within seemingly simple mathematical puzzles. This exercise serves as a potent reminder that even the simplest-looking sequences can hold hidden complexity and inspire us to hone our analytical skills. The journey of exploring potential solutions, even without reaching a single definitive answer, enriches our understanding of mathematical principles and strengthens our problem-solving capabilities.
Latest Posts
Latest Posts
-
A Economy Usually Stresses The Equality Of All Citizens
Jun 05, 2025
-
Describe Two Games That Are Typical Of The Gaucho Games
Jun 05, 2025
-
A Customer Uses An App To Order Pizza For Delivery
Jun 05, 2025
-
Both Teams Uniforms Are Purple And White
Jun 05, 2025
-
Which Sentence Accurately Describes Star Clusters
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about Solve For The Variable In 7 28 25 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.