Solve For X 7x 4x 27
Breaking News Today
Jun 05, 2025 · 5 min read
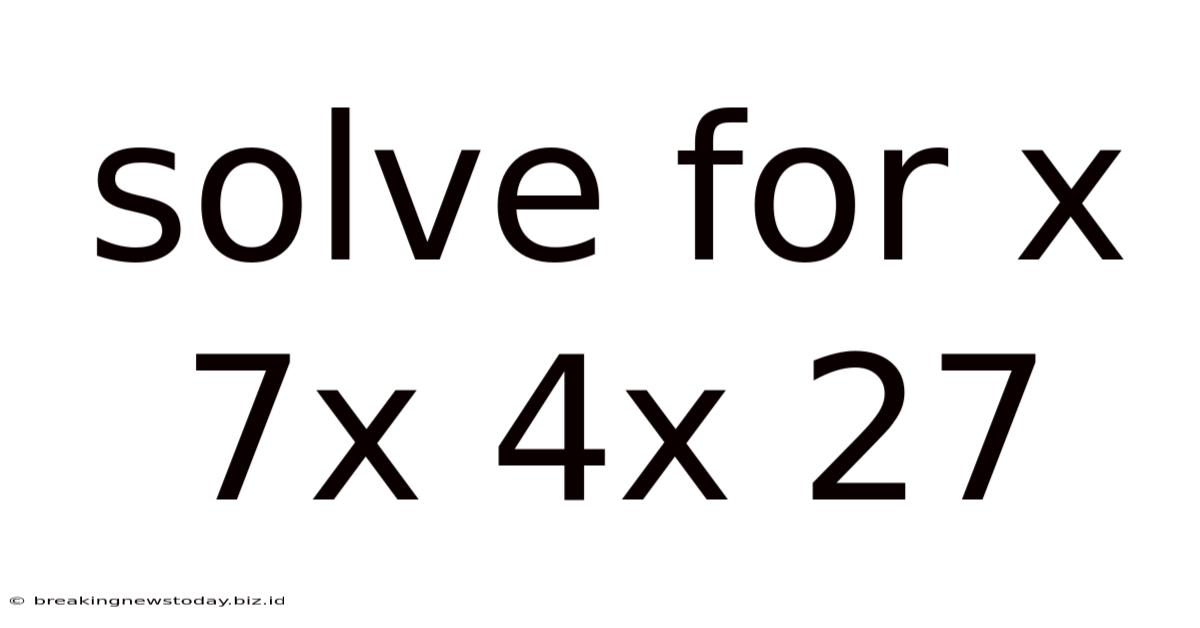
Table of Contents
Solving for x: A Deep Dive into 7x + 4x = 27 and Beyond
This article will delve into the seemingly simple equation 7x + 4x = 27, providing a comprehensive explanation of its solution and exploring broader concepts in algebra related to solving for 'x'. We'll move beyond the immediate solution to examine similar problems, discuss different approaches, and consider potential pitfalls to avoid. This detailed explanation will be useful for students learning algebra, as well as anyone looking to refresh their understanding of fundamental algebraic principles.
Understanding the Equation: 7x + 4x = 27
The equation 7x + 4x = 27 is a linear equation in one variable, 'x'. This means it involves only one variable raised to the power of one, and there are no other complex operations like squares, cubes, or roots. The goal is to isolate 'x' on one side of the equation to determine its value.
What does 7x and 4x mean?
Before solving, let's clarify the meaning of terms like 7x and 4x. In algebra, the number placed directly before a variable (called the coefficient) signifies multiplication. So, 7x actually means 7 multiplied by x, and 4x means 4 multiplied by x.
Solving the Equation: Step-by-Step Guide
The solution involves combining like terms and then isolating 'x'. Here's a step-by-step breakdown:
Step 1: Combine Like Terms
The terms 7x and 4x are "like terms" because they both contain the variable x raised to the same power (in this case, the power is 1). We can combine these terms by adding their coefficients:
7x + 4x = (7 + 4)x = 11x
This simplifies our equation to:
11x = 27
Step 2: Isolate x
To isolate 'x', we need to get rid of the coefficient 11. Since 11 is multiplied by x, we perform the inverse operation, which is division. We divide both sides of the equation by 11:
11x / 11 = 27 / 11
This simplifies to:
x = 27/11
Step 3: Simplify the Fraction (if possible)
In this case, the fraction 27/11 is already in its simplest form, as 27 and 11 share no common factors other than 1. Therefore, the solution remains:
x = 27/11
Step 4: Verify the solution
It's always a good practice to verify the solution by substituting the value of x back into the original equation:
7(27/11) + 4(27/11) = 27
189/11 + 108/11 = 27
297/11 = 27
27 = 27
Since the equation holds true, our solution x = 27/11 is correct.
Expanding on the Concept: Different Types of Equations
While 7x + 4x = 27 is a straightforward example, let's explore more complex scenarios to build a stronger understanding of solving for 'x'.
Equations with Parentheses
Consider an equation like:
3(x + 2) = 15
Step 1: Distribute
First, we need to distribute the 3 to both terms inside the parentheses:
3 * x + 3 * 2 = 15
3x + 6 = 15
Step 2: Isolate the term with 'x'
Subtract 6 from both sides:
3x = 9
Step 3: Solve for 'x'
Divide both sides by 3:
x = 3
Equations with Fractions
Let's look at an equation involving fractions:
x/2 + x/4 = 3
Step 1: Find a Common Denominator
The common denominator for 2 and 4 is 4. Rewrite the fractions with this common denominator:
2x/4 + x/4 = 3
Step 2: Combine Like Terms
Combine the fractions:
3x/4 = 3
Step 3: Solve for 'x'
Multiply both sides by 4:
3x = 12
Divide both sides by 3:
x = 4
Equations with Decimals
Equations can also include decimals. For example:
0.5x + 1.5x = 10
Step 1: Combine Like Terms
Add the coefficients of x:
2x = 10
Step 2: Solve for 'x'
Divide both sides by 2:
x = 5
Advanced Techniques: Systems of Equations and Quadratic Equations
While the initial equation was simple, solving for x can become significantly more complex. Let's briefly touch upon two advanced scenarios:
Systems of Equations
A system of equations involves multiple equations with multiple variables. For example:
x + y = 5 x - y = 1
Solving this system requires techniques like substitution or elimination to find the values of both x and y.
Quadratic Equations
Quadratic equations involve x raised to the power of 2. A typical quadratic equation looks like:
ax² + bx + c = 0
Solving for x in a quadratic equation involves techniques like factoring, completing the square, or using the quadratic formula.
Common Mistakes to Avoid When Solving for x
Several common mistakes can lead to incorrect solutions. Here are a few to watch out for:
- Incorrect order of operations: Always follow the order of operations (PEMDAS/BODMAS) – Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- Errors in combining like terms: Ensure that you correctly add or subtract like terms. A simple arithmetic error can lead to a wrong answer.
- Mistakes in arithmetic: Double-check your calculations throughout the process.
- Forgetting to perform the same operation on both sides: Remember that whatever you do to one side of the equation, you must do to the other side to maintain balance.
- Incorrect simplification of fractions: Simplify fractions to their lowest terms for an accurate final answer.
Practice Makes Perfect
The best way to improve your ability to solve for x is through practice. Work through various types of equations, gradually increasing their complexity. Start with simple linear equations and then move on to more challenging problems. Use online resources, textbooks, and practice exercises to hone your skills.
Conclusion: Mastering the Art of Solving for x
Solving for x is a fundamental skill in algebra and mathematics as a whole. While the initial equation 7x + 4x = 27 might seem trivial, understanding its solution provides a solid foundation for tackling more complex algebraic problems. By mastering the basic principles, practicing regularly, and being mindful of common mistakes, you can develop proficiency in solving for x and confidently tackle a wide range of mathematical challenges. Remember that consistent practice and attention to detail are key to success in algebra.
Latest Posts
Latest Posts
-
A Shipping Container Will Be Used To Transport Several 40 Kilogram
Jun 06, 2025
-
Drag The Numbers To Order Them From Least To Greatest
Jun 06, 2025
-
Clase De Contabilidad Ser 11 45 A M
Jun 06, 2025
-
Honors Algebra 2 13 4 Sine And Cosine Graphs Worksheet
Jun 06, 2025
-
Determine The Stability Of Each Ecosystem
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Solve For X 7x 4x 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.