Solve The Compound Inequality 3x-4 5 Or 1-2x 7
Breaking News Today
Jun 07, 2025 · 5 min read
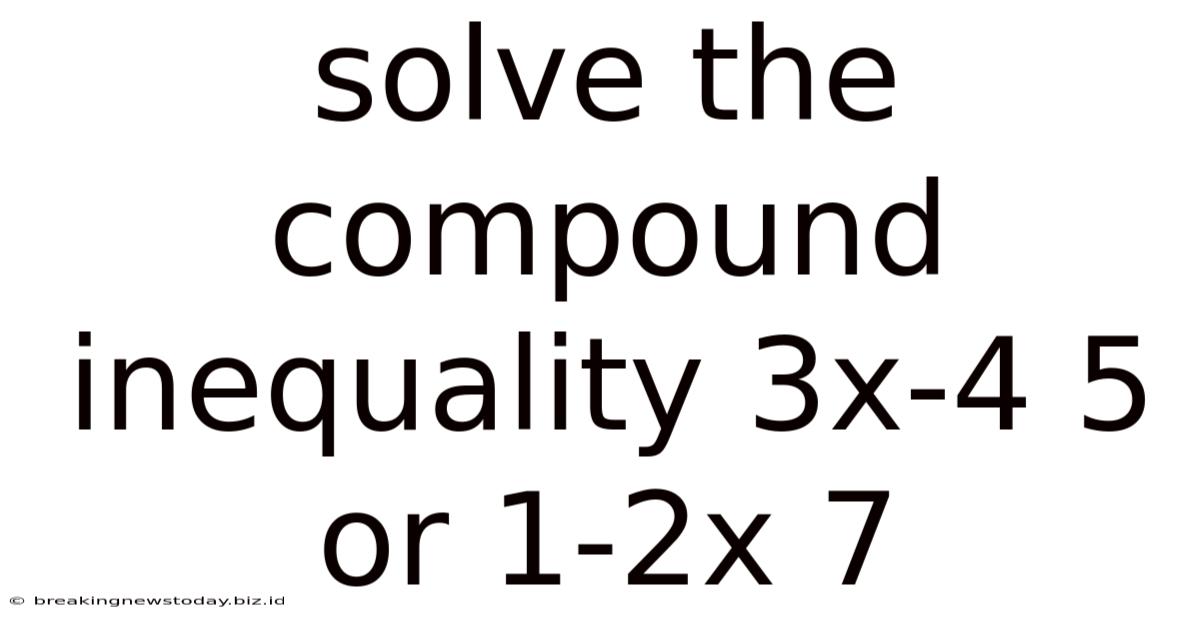
Table of Contents
Solving Compound Inequalities: A Comprehensive Guide
Compound inequalities, as their name suggests, involve more than one inequality linked together. They often present a challenge for students learning algebra, but mastering them is crucial for success in higher-level math. This article will provide a thorough explanation of how to solve compound inequalities, focusing on the specific example: 3x - 4 > 5 or 1 - 2x ≥ 7. We'll break down the process step-by-step, offering tips and tricks for accuracy and efficiency, and exploring the broader context of compound inequalities in mathematics.
Understanding Compound Inequalities
A compound inequality combines two or more inequalities using the words "and" or "or." The word used significantly impacts how we solve and represent the solution.
-
"And" Inequalities: The solution to an "and" inequality must satisfy both inequalities simultaneously. Graphically, this is represented by the intersection of the solution sets of the individual inequalities.
-
"Or" Inequalities: The solution to an "or" inequality must satisfy at least one of the inequalities. Graphically, this is represented by the union of the solution sets of the individual inequalities.
Our example, 3x - 4 > 5 or 1 - 2x ≥ 7, is an "or" inequality. This means we need to find the values of x that satisfy either the first inequality or the second inequality (or both).
Solving the First Inequality: 3x - 4 > 5
Let's tackle the first inequality: 3x - 4 > 5. Our goal is to isolate x.
-
Add 4 to both sides: This eliminates the constant term on the left side.
3x - 4 + 4 > 5 + 43x > 9 -
Divide both sides by 3: This isolates x. Remember, when dividing or multiplying by a negative number, you must flip the inequality sign. Since we're dividing by a positive number, the sign stays the same.
3x / 3 > 9 / 3x > 3
This tells us that the first inequality is satisfied for all values of x greater than 3.
Solving the Second Inequality: 1 - 2x ≥ 7
Now let's solve the second inequality: 1 - 2x ≥ 7.
-
Subtract 1 from both sides:
1 - 2x - 1 ≥ 7 - 1-2x ≥ 6 -
Divide both sides by -2: Crucially, since we're dividing by a negative number, we must reverse the inequality sign.
-2x / -2 ≤ 6 / -2x ≤ -3
This means the second inequality is satisfied for all values of x less than or equal to -3.
Combining the Solutions: The "Or" Condition
Because our original compound inequality uses "or," we need to combine the solution sets of both individual inequalities. The solution is the union of these sets.
The first inequality gave us x > 3, and the second gave us x ≤ -3. Therefore, the solution to the compound inequality 3x - 4 > 5 or 1 - 2x ≥ 7 is:
x > 3 or x ≤ -3
This means any value of x that is either greater than 3 or less than or equal to -3 satisfies the compound inequality.
Graphical Representation
Visualizing the solution set is often helpful. We can represent the solution on a number line:
<-------------------o=================>
-3 3
The closed circle at -3 indicates that -3 is included in the solution set, while the open circle at 3 indicates that 3 is not included. The shaded regions represent the values of x that satisfy the inequality.
Interval Notation
Another way to express the solution is using interval notation. This notation uses parentheses and brackets to denote open and closed intervals.
- Open interval: (a, b) represents all numbers between a and b, excluding a and b.
- Closed interval: [a, b] represents all numbers between a and b, including a and b.
- Half-open intervals: (a, b] or [a, b) represent intervals including one endpoint but not the other.
For our solution, x > 3 or x ≤ -3, the interval notation is:
(-∞, -3] ∪ (3, ∞)
The symbol "∪" represents the union of the two intervals. (-∞, -3] represents all numbers from negative infinity up to and including -3, while (3, ∞) represents all numbers from 3 to positive infinity.
Advanced Considerations and Applications
Understanding compound inequalities is fundamental to various mathematical concepts and applications. Let's delve into some more nuanced aspects:
1. "And" Inequalities: A Contrast
To fully grasp the concept, let's briefly consider an "and" inequality. Suppose we had:
2x + 1 > -3 and x - 4 < 2
Solving each inequality separately yields:
x > -2 and x < 6
The solution for an "and" inequality is the intersection of both solution sets. This means x must be both greater than -2 and less than 6. Graphically, this would be a segment on the number line between -2 and 6, excluding -2 and 6 themselves. The interval notation would be (-2, 6).
2. Absolute Value Inequalities
Absolute value inequalities often result in compound inequalities. For example:
|x - 2| < 5
This inequality is equivalent to:
-5 < x - 2 < 5
Solving this yields:
-3 < x < 7
3. Real-World Applications
Compound inequalities are frequently applied in real-world scenarios. For instance, in manufacturing, tolerances often involve ranges. A component might be acceptable if its length is between 10 cm and 10.2 cm, representable by a compound inequality. In finance, compound inequalities are used to model interest rate ranges or investment thresholds.
4. Advanced Algebra and Calculus
The principles of solving compound inequalities are foundational for more advanced algebraic manipulations and are crucial in understanding concepts like piecewise functions, which are commonly encountered in calculus. Piecewise functions define different expressions for different intervals of the independent variable, often expressed using compound inequalities to specify those intervals.
Conclusion: Mastering Compound Inequalities
Solving compound inequalities requires a systematic approach involving careful attention to detail, particularly when dealing with negative coefficients and the distinctions between "and" and "or" conditions. By understanding the underlying principles and employing the steps outlined in this guide, you'll gain confidence in tackling these types of problems. Furthermore, appreciating the broader context of compound inequalities within mathematics will enhance your overall mathematical understanding and provide a strong foundation for more advanced studies. Remember to practice regularly – the more you practice, the more proficient you’ll become!
Latest Posts
Latest Posts
-
An Insurance Agent Visits A Potential Client
Jun 07, 2025
-
Unit 7 Polynomials And Factoring Homework 3 Answer Key
Jun 07, 2025
-
What Do Custom Filters Provide That Autofilters Dont
Jun 07, 2025
-
Which Statement Best Represents The Philosophy Of Legalism
Jun 07, 2025
-
Which Correctly Lists Three Main Causes Of Deforestation
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Solve The Compound Inequality 3x-4 5 Or 1-2x 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.