Solve The Compound Inequality 6b 24 Or 4b 12 4
Breaking News Today
Jun 04, 2025 · 5 min read
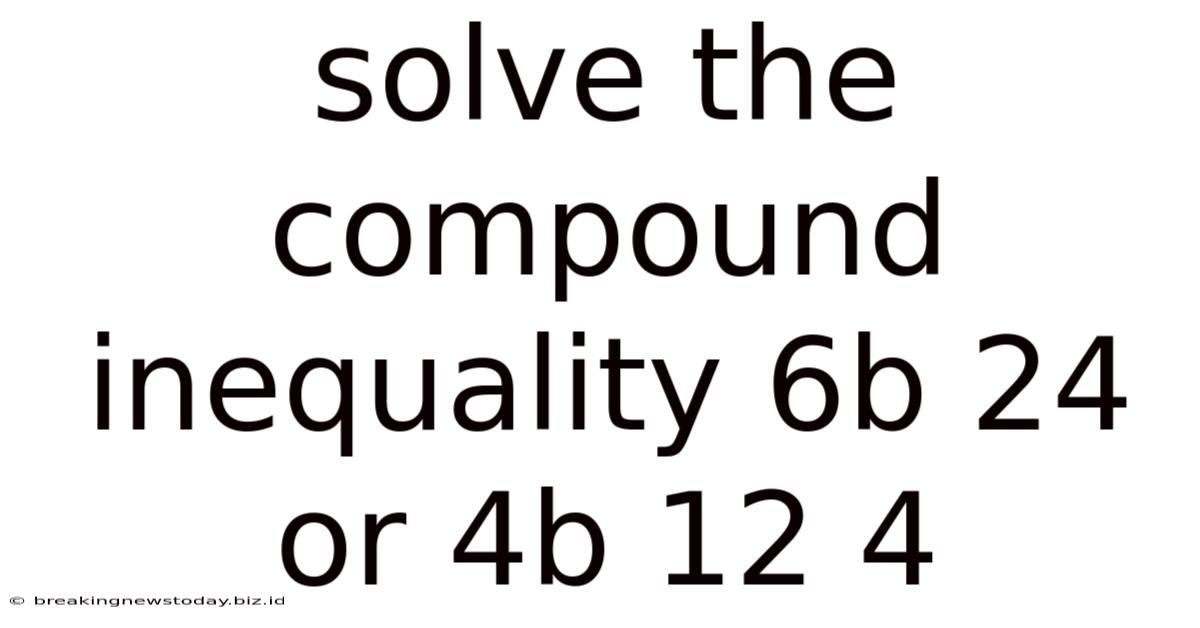
Table of Contents
Solving Compound Inequalities: A Comprehensive Guide
Compound inequalities involve two or more inequalities joined by "and" or "or." Solving them requires a nuanced approach compared to single inequalities. This comprehensive guide will delve into the strategies and techniques for solving compound inequalities, particularly focusing on the example: 6b ≥ 24 or 4b + 12 ≤ 4. We'll break down the process step-by-step, explore the graphical representation, and discuss the implications of using "or" versus "and" in compound inequalities.
Understanding Compound Inequalities
A compound inequality combines two or more inequalities. The connecting word, "and" or "or," significantly impacts the solution set.
-
"And" inequalities: The solution must satisfy both inequalities simultaneously. The solution set is the intersection of the individual solution sets.
-
"Or" inequalities: The solution must satisfy at least one of the inequalities. The solution set is the union of the individual solution sets.
Our example, 6b ≥ 24 or 4b + 12 ≤ 4, is an "or" inequality. This means we need to find the values of 'b' that satisfy either 6b ≥ 24 or 4b + 12 ≤ 4, or both.
Solving the First Inequality: 6b ≥ 24
This is a simple linear inequality. To solve for 'b', we isolate 'b' by dividing both sides of the inequality by 6:
6b ≥ 24
b ≥ 24/6
b ≥ 4
This means that any value of 'b' greater than or equal to 4 satisfies this inequality.
Solving the Second Inequality: 4b + 12 ≤ 4
To solve this linear inequality, we follow these steps:
-
Subtract 12 from both sides: This isolates the term with 'b'.
4b + 12 ≤ 4 4b ≤ 4 - 12 4b ≤ -8 -
Divide both sides by 4: Remember, when dividing or multiplying an inequality by a negative number, you must reverse the inequality sign. In this case, we're dividing by a positive number, so the inequality sign remains the same.
4b ≤ -8 b ≤ -8/4 b ≤ -2
This means that any value of 'b' less than or equal to -2 satisfies this inequality.
Combining the Solutions: The "Or" Condition
Since our original compound inequality uses "or," the solution set includes all values of 'b' that satisfy either b ≥ 4 or b ≤ -2. This means our solution is the union of the two individual solution sets.
In interval notation, the solution is: (-∞, -2] ∪ [4, ∞).
This notation indicates that 'b' can be any value from negative infinity up to and including -2, or any value from 4 up to positive infinity.
Graphical Representation
Graphing the solution helps visualize the solution set. We would typically use a number line:
<-------------------|-------------------|------------------->
-2 0 4
[=======) (=======]
The closed circles at -2 and 4 indicate that these values are included in the solution set. The lines extending to the left from -2 and to the right from 4 represent all values less than or equal to -2 and greater than or equal to 4, respectively.
Contrast with "And" Inequalities
Let's contrast this with an "and" inequality. Consider the compound inequality:
6b ≥ 24 and 4b + 12 ≤ 4
To solve this, we find the solution sets for each inequality individually, as we did before: b ≥ 4 and b ≤ -2.
However, because this is an "and" inequality, the solution must satisfy both conditions simultaneously. There are no values of 'b' that are simultaneously greater than or equal to 4 and less than or equal to -2. Therefore, the solution set for this "and" inequality is the empty set, denoted by {} or Ø.
Solving More Complex Compound Inequalities
The techniques described above can be extended to solve more complex compound inequalities. These might involve:
-
More than two inequalities: The principles of "and" and "or" extend to compound inequalities with three or more parts. For "and" inequalities, the solution must satisfy all conditions. For "or" inequalities, satisfying at least one condition is sufficient.
-
Nonlinear inequalities: Inequalities involving quadratic expressions, absolute values, or other non-linear functions require different solution techniques. These often involve factoring, the quadratic formula, or considering different cases based on the nature of the non-linear function.
-
Inequalities with multiple variables: While the focus here has been on single-variable inequalities, the same principles can apply to compound inequalities involving multiple variables. The solution will then typically be a region in a multi-dimensional space.
Real-World Applications of Compound Inequalities
Compound inequalities frequently appear in real-world scenarios. Here are a few examples:
-
Manufacturing tolerances: In manufacturing, compound inequalities are used to specify acceptable ranges for dimensions or other product characteristics. A product might be acceptable if its length is between 10cm and 12cm (inclusive), expressed as 10 ≤ L ≤ 12.
-
Financial modeling: Compound inequalities might be used to define different tax brackets or investment strategies based on income levels or asset values.
-
Temperature control: Thermostats use compound inequalities to maintain a desired temperature range in a building. The heating or cooling system activates when the temperature falls below a lower limit or rises above an upper limit.
-
Scientific research: In experimental science, compound inequalities are used to define ranges of acceptable values for experimental variables or results.
Checking Your Solutions
It's crucial to always check your solutions. Substitute a few values from your solution set back into the original compound inequality to confirm they satisfy the conditions. For example, if you believe the solution is b ≥ 4, test values like b=4, b=5, and b=10. Similarly, if you believe the solution is b ≤ -2, test values like b=-2, b=-3, and b=-10. This step helps identify and correct potential errors in your calculations.
Conclusion
Solving compound inequalities requires a clear understanding of the "and" and "or" operators, a systematic approach to solving individual inequalities, and careful attention to the properties of inequalities. By mastering these techniques, you can confidently tackle a wide range of compound inequality problems and apply them to solve real-world problems across various disciplines. Remember to always check your solutions to ensure accuracy and build confidence in your mathematical abilities. The graphical representation is a powerful tool for visualizing and understanding the solution sets, especially for those who are visual learners. Practicing diverse problems will further enhance your skills in solving compound inequalities effectively.
Latest Posts
Latest Posts
-
Rates People On Seven Orientation Scales
Jun 06, 2025
-
What Type Of Angle Is 119
Jun 06, 2025
-
45621 Rounded To The Nearest Ten Thousand
Jun 06, 2025
-
Find X Round Your Answer To The Nearest Integer
Jun 06, 2025
-
Quiz 4 1 Classifying And Solving For Sides Angles In Triangles Answers
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Solve The Compound Inequality 6b 24 Or 4b 12 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.