Solve The Equation 9x 1 X 17
Breaking News Today
Jun 01, 2025 · 5 min read
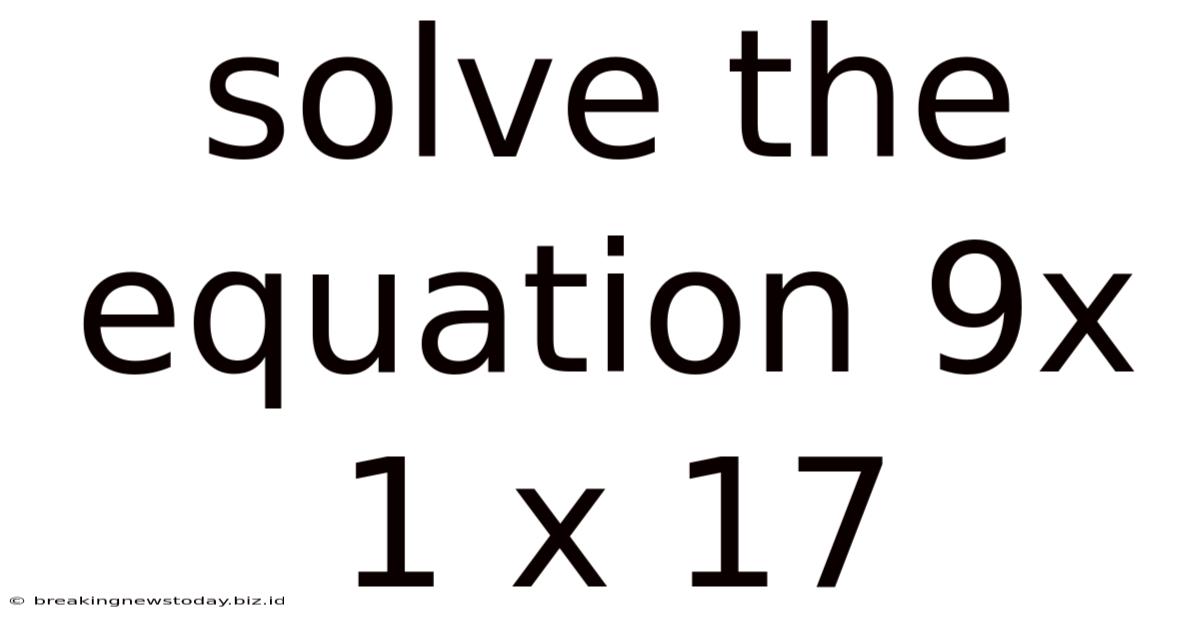
Table of Contents
Decoding the Equation: A Comprehensive Guide to Solving 9x + 1 = 17
This article delves deep into solving the seemingly simple algebraic equation, 9x + 1 = 17. While the solution might appear straightforward to experienced mathematicians, understanding the underlying principles and applying various methods is crucial for building a strong foundation in algebra. We will explore several approaches to solving this equation, emphasizing the logic and reasoning behind each step, making it accessible to both beginners and those seeking a refresher. We’ll also explore the broader context of linear equations and their applications in the real world.
Understanding the Fundamentals: What are Linear Equations?
Before jumping into the solution, let’s establish a clear understanding of what linear equations are. A linear equation is an algebraic equation in which the highest power of the variable (in this case, 'x') is 1. They represent a straight line when graphed on a coordinate plane. The general form of a linear equation with one variable is:
ax + b = c
Where:
- a, b, and c are constants (numbers).
- x is the variable we need to solve for.
Our equation, 9x + 1 = 17, perfectly fits this general form, with a = 9, b = 1, and c = 17.
Method 1: The Isolation Method – A Step-by-Step Approach
The most common and intuitive method for solving linear equations is the isolation method. This involves manipulating the equation to isolate the variable 'x' on one side of the equation, leaving its value on the other. Here’s how it works for our equation:
-
Subtract 1 from both sides: Our goal is to get 'x' by itself. Since 1 is added to 9x, we subtract 1 from both sides of the equation to maintain balance:
9x + 1 - 1 = 17 - 1
This simplifies to:
9x = 16
-
Divide both sides by 9: Now, 'x' is multiplied by 9. To isolate 'x', we divide both sides of the equation by 9:
9x / 9 = 16 / 9
This gives us the solution:
x = 16/9 or x ≈ 1.778
Therefore, the solution to the equation 9x + 1 = 17 is x = 16/9.
Method 2: Using Inverse Operations – A More Conceptual Approach
This method focuses on the concept of inverse operations. Every mathematical operation has an inverse: addition and subtraction are inverses, as are multiplication and division. To solve for 'x', we apply the inverse operations in reverse order of operations (PEMDAS/BODMAS).
-
Inverse of Addition: Since 1 is added to 9x, we perform the inverse operation – subtraction – by subtracting 1 from both sides. This mirrors step 1 of the isolation method.
-
Inverse of Multiplication: 'x' is multiplied by 9. The inverse operation is division. We divide both sides by 9, mirroring step 2 of the isolation method.
This method reinforces the understanding that solving equations is about undoing the operations performed on the variable.
Method 3: Graphical Representation – Visualizing the Solution
While not directly solving the equation, visualizing it graphically provides a powerful way to understand the solution. We can represent the equation 9x + 1 = 17 as two separate functions:
- y = 9x + 1
- y = 17
Graphing these two functions on a coordinate plane will show their intersection point. The x-coordinate of this intersection point represents the solution to the equation. The intersection occurs where the line y = 9x + 1 intersects the horizontal line y = 17. The x-value at this point will be 16/9. This graphical method offers a visual confirmation of the algebraic solution.
Verifying the Solution – Ensuring Accuracy
It’s crucial to verify the solution to ensure accuracy. Substitute the value of x (16/9) back into the original equation:
9 * (16/9) + 1 = 17
Simplifying:
16 + 1 = 17
17 = 17
Since the equation holds true, our solution, x = 16/9, is correct.
Expanding the Scope: Applications of Linear Equations
Linear equations are fundamental to various fields. Their applications span:
- Physics: Describing relationships between physical quantities like velocity, acceleration, and time.
- Engineering: Modeling linear systems, calculating forces, and designing structures.
- Economics: Representing supply and demand curves, forecasting economic trends.
- Computer Science: Developing algorithms and modeling linear relationships in data.
- Everyday Life: Calculating costs, determining distances, and solving proportion problems.
Beyond the Basics: Solving More Complex Linear Equations
While this article focuses on a simple equation, the principles discussed extend to more complex scenarios. Equations with fractions, decimals, or multiple variables can be solved using similar techniques, often involving additional steps to simplify the equation before isolating the variable.
Mastering Linear Equations: Tips and Practice
Developing proficiency in solving linear equations requires consistent practice. Here are some helpful tips:
- Practice Regularly: Consistent practice is key to mastering any mathematical concept.
- Start with Simple Equations: Gradually increase the complexity of equations as your understanding grows.
- Understand the Concepts: Don't just memorize steps; understand the underlying principles.
- Check Your Answers: Always verify your solutions by substituting them back into the original equation.
- Utilize Online Resources: Many websites and apps offer practice problems and tutorials on linear equations.
Conclusion: A Foundation for Further Mathematical Exploration
Solving the equation 9x + 1 = 17, while seemingly basic, serves as a foundational stepping stone in algebra. Understanding the methods and concepts presented here will empower you to tackle more complex equations and apply the principles of linear algebra to various real-world problems. Remember, consistent practice and a grasp of fundamental concepts are the keys to success in mathematics. By mastering these basic skills, you'll open doors to more advanced mathematical concepts and their applications in numerous fields. So, continue practicing and exploring, and watch your mathematical abilities flourish!
Latest Posts
Latest Posts
-
In What Country Are Fireworks Used As A Distraction
Jun 02, 2025
-
Repeated Demonstrations Are A Hallmark Of Which Of The Following
Jun 02, 2025
-
The Primary Organizational Buying Objective For Business Firms Is To
Jun 02, 2025
-
Which Of The Following Indicates The Stern Of This Vessel
Jun 02, 2025
-
Write A Statement That Assigns Middleinitial With The Character T
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about Solve The Equation 9x 1 X 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.