Solve The Equation Log6 13 X 1 X
Breaking News Today
May 11, 2025 · 4 min read
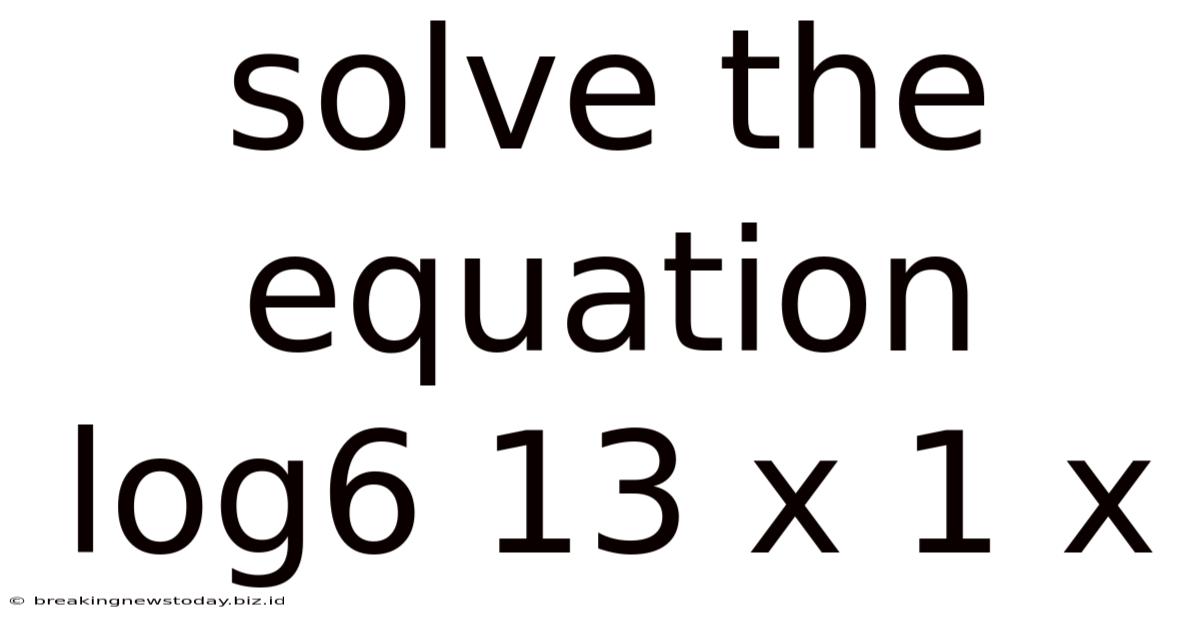
Table of Contents
Solving the Equation: log₆(13x) = 1
This article delves into the solution of the logarithmic equation log₆(13x) = 1. We'll explore the fundamental principles of logarithms, demonstrate the step-by-step solution process, and discuss various approaches to solving similar logarithmic equations. Understanding logarithmic equations is crucial in various fields, including mathematics, science, and engineering, as they are frequently used to model exponential relationships.
Understanding Logarithms
Before tackling the equation, let's revisit the core concept of logarithms. A logarithm is essentially the inverse operation of exponentiation. The equation logₐ(b) = c means that a<sup>c</sup> = b. In other words, the logarithm of b to base a is the exponent c to which a must be raised to obtain b.
In our equation, log₆(13x) = 1, the base is 6, the argument is 13x, and the result is 1. This implies that 6<sup>1</sup> = 13x.
Step-by-Step Solution
-
Rewrite the Equation in Exponential Form: The first step in solving log₆(13x) = 1 is to rewrite the logarithmic equation in its equivalent exponential form. As explained above, this gives us:
6<sup>1</sup> = 13x
-
Simplify the Equation: The left side of the equation simplifies to 6, resulting in a simple algebraic equation:
6 = 13x
-
Solve for x: To isolate x, we divide both sides of the equation by 13:
x = 6/13
Therefore, the solution to the equation log₆(13x) = 1 is x = 6/13.
Verifying the Solution
It's always a good practice to verify our solution by substituting the value of x back into the original equation:
log₆(13 * (6/13)) = log₆(6) = 1
Since the equation holds true, our solution x = 6/13 is correct.
Alternative Approaches and Considerations
While the above method provides a straightforward solution, let's explore other approaches and potential challenges when solving logarithmic equations.
1. Using the Change of Base Formula
The change of base formula allows you to convert a logarithm from one base to another. This can be particularly useful if you're working with a calculator that doesn't directly support the base-6 logarithm. The formula is:
logₐ(b) = logₓ(b) / logₓ(a)
where x is any convenient base, often 10 or e (the natural logarithm base). Applying this to our equation:
log₆(13x) = log₁₀(13x) / log₁₀(6) = 1
This equation can then be solved for x using algebraic manipulation, although it's generally more complex than the direct approach.
2. Dealing with Logarithmic Properties
More complex logarithmic equations often require the application of logarithmic properties. These properties include:
- Product Rule: logₐ(mn) = logₐ(m) + logₐ(n)
- Quotient Rule: logₐ(m/n) = logₐ(m) - logₐ(n)
- Power Rule: logₐ(m<sup>n</sup>) = n * logₐ(m)
These rules can be used to simplify equations before solving for the unknown variable. For instance, if you encountered an equation like log₂(x) + log₂(x+1) = 1, you would use the product rule to simplify it before solving.
3. Handling Equations with Multiple Logarithms
Equations containing multiple logarithms often require careful manipulation using logarithmic properties. For example, consider the equation:
log₃(x) + log₃(x-2) = 1
Here, you would first use the product rule to combine the logarithms:
log₃(x(x-2)) = 1
Then, rewrite in exponential form and solve the resulting quadratic equation.
4. Extraneous Solutions
It’s crucial to check for extraneous solutions. These are solutions that satisfy the simplified equation but not the original logarithmic equation. This often happens when manipulating logarithms, particularly when dealing with the arguments of logarithms. Remember that the argument of a logarithm must always be positive. Any solution that leads to a negative or zero argument must be discarded. Always verify your solutions by substituting them back into the original equation.
5. No Solution Scenarios
Some logarithmic equations might have no solution. This occurs when the manipulations lead to a contradiction, such as a negative argument inside a logarithm or an impossible equation.
Expanding on Logarithmic Applications
Logarithms have wide-ranging applications in diverse fields:
- Chemistry: Calculating pH values (pH = -log[H+])
- Physics: Measuring sound intensity (decibels) and earthquake magnitudes (Richter scale).
- Finance: Calculating compound interest and exponential growth/decay models.
- Computer Science: Analyzing algorithm complexities and data structures.
- Engineering: Modeling signal attenuation and other exponential processes.
Understanding and solving logarithmic equations is fundamental to grasping these applications.
Advanced Logarithmic Equation Solving Techniques
For more complex equations, numerical methods such as the Newton-Raphson method might be necessary. These iterative techniques provide approximate solutions when algebraic methods are insufficient. Furthermore, graphical methods using graphing calculators or software can be valuable tools to visualize the equation and identify potential solutions.
Conclusion
Solving the equation log₆(13x) = 1 demonstrates a fundamental skill in mathematics. The straightforward approach outlined above, combined with a deep understanding of logarithmic principles and potential pitfalls, equips you to tackle a wide range of logarithmic equations, both simple and complex. Remember to always verify your solutions and be mindful of potential extraneous solutions or cases with no solutions. The ability to solve these equations opens doors to a deeper comprehension of many scientific and engineering concepts and their applications.
Latest Posts
Latest Posts
-
A Line That Is A Continuous Mark Is
May 12, 2025
-
Label The Structures Of The Male Urinary Tract
May 12, 2025
-
What Are Your Roles In The At Program
May 12, 2025
-
A Receptacle Under A Sink Would Require
May 12, 2025
-
Pathogenic Bacteria Are Responsible For All Of The Following Except
May 12, 2025
Related Post
Thank you for visiting our website which covers about Solve The Equation Log6 13 X 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.