Solve This Inequality 3q 11 8q 99
Breaking News Today
Jun 07, 2025 · 5 min read
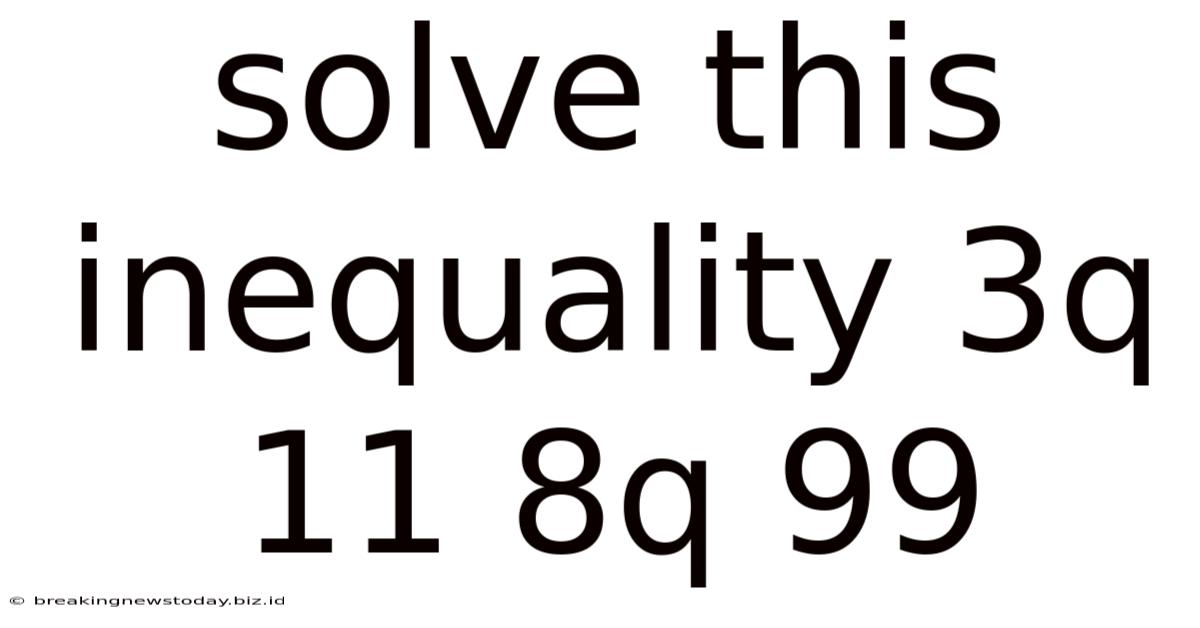
Table of Contents
Solving the Inequality: 3q + 11 > 8q - 99
This article provides a comprehensive guide on how to solve the inequality 3q + 11 > 8q - 99, explaining each step in detail and exploring related concepts. We will not only find the solution but also delve into the underlying principles of solving inequalities, offering practical tips and strategies for similar problems. Understanding inequalities is crucial in various mathematical fields, and this guide aims to build a strong foundational understanding.
Understanding Inequalities
Before we dive into the solution, let's refresh our understanding of inequalities. An inequality is a mathematical statement that compares two expressions using inequality symbols:
- >: Greater than
- <: Less than
- ≥: Greater than or equal to
- ≤: Less than or equal to
Unlike equations, which have a single solution (or a finite number of solutions), inequalities often have an infinite number of solutions, represented as a range or interval.
Steps to Solve 3q + 11 > 8q - 99
The key to solving inequalities is to manipulate them algebraically, similar to solving equations, while carefully considering the impact of the inequality symbol. Here's a step-by-step approach to solving 3q + 11 > 8q - 99:
Step 1: Gather the Variables
Our goal is to isolate the variable 'q' on one side of the inequality. To begin, let's gather all the terms containing 'q' on one side and the constant terms on the other. We can achieve this by subtracting 3q from both sides:
3q + 11 - 3q > 8q - 99 - 3q
This simplifies to:
11 > 5q - 99
Step 2: Isolate the Constant Term
Next, let's isolate the term with 'q' by adding 99 to both sides of the inequality:
11 + 99 > 5q - 99 + 99
This simplifies to:
110 > 5q
Step 3: Solve for 'q'
Now, we need to solve for 'q' by dividing both sides by 5. Crucially, remember that when you divide or multiply an inequality by a negative number, you must reverse the inequality sign. Since we are dividing by a positive number (5), we don't need to reverse the sign:
110/5 > 5q/5
This simplifies to:
22 > q
Step 4: Express the Solution
The solution to the inequality 3q + 11 > 8q - 99 is q < 22. This means that any value of 'q' less than 22 will satisfy the original inequality. We can represent this solution on a number line, using an open circle at 22 (because q is strictly less than 22, not less than or equal to) and shading the region to the left.
Representing the Solution Set
The solution set, q < 22, can be represented in several ways:
- Inequality Notation: q < 22
- Interval Notation: (-∞, 22) The parenthesis indicates that 22 is not included in the solution set.
- Number Line: A number line with an open circle at 22 and the region to the left shaded.
Verifying the Solution
To verify our solution, we can test values of 'q' within the solution set (q < 22) and outside the solution set (q ≥ 22).
Test Value 1 (Inside the Solution Set): q = 20
Substituting q = 20 into the original inequality:
3(20) + 11 > 8(20) - 99
60 + 11 > 160 - 99
71 > 61 (True)
Test Value 2 (Outside the Solution Set): q = 25
Substituting q = 25 into the original inequality:
3(25) + 11 > 8(25) - 99
75 + 11 > 200 - 99
86 > 101 (False)
These tests confirm that our solution, q < 22, is correct.
Advanced Concepts and Related Problems
This simple inequality provides a solid foundation for understanding more complex inequalities. Let's explore some related concepts and problems:
Compound Inequalities
Compound inequalities involve two or more inequalities combined with "and" or "or." For example:
2x + 5 > 11 and 3x - 2 < 10
To solve a compound inequality with "and," you solve each inequality separately and find the intersection of the solution sets. For "or," you find the union of the solution sets.
Absolute Value Inequalities
Absolute value inequalities involve the absolute value function |x|. Solving these requires considering both positive and negative cases. For example:
|2x - 3| < 5
This inequality is equivalent to -5 < 2x - 3 < 5. You would solve this compound inequality to find the solution set.
Quadratic Inequalities
Quadratic inequalities involve quadratic expressions (e.g., ax² + bx + c). Solving these often involves finding the roots of the corresponding quadratic equation and testing intervals to determine the solution set.
Applications of Inequalities
Inequalities have widespread applications in various fields, including:
- Optimization Problems: Finding maximum or minimum values.
- Physics: Describing ranges of values for physical quantities.
- Economics: Modeling constraints and resource allocation.
- Computer Science: Designing algorithms and data structures.
Tips for Solving Inequalities
- Always check your work: Test values within and outside the solution set to verify your answer.
- Be mindful of the inequality symbol: Remember to reverse the symbol when multiplying or dividing by a negative number.
- Practice regularly: The more you practice, the more comfortable you'll become with solving inequalities of different types.
- Understand the underlying principles: Focus on the logic behind each step, not just memorizing procedures.
Conclusion
Solving the inequality 3q + 11 > 8q - 99 involves a straightforward process of manipulating the inequality algebraically to isolate the variable 'q.' The solution, q < 22, represents the range of values for 'q' that satisfy the inequality. Understanding the principles of solving inequalities, including the impact of multiplying or dividing by negative numbers, is crucial for tackling more complex problems and applying inequalities to various real-world scenarios. By mastering these techniques and practicing regularly, you'll develop a strong foundation in algebra and problem-solving. Remember to verify your solutions and explore more advanced topics like compound inequalities, absolute value inequalities, and quadratic inequalities to deepen your understanding. This comprehensive guide has equipped you with the knowledge and tools to confidently approach and solve a wide range of inequalities.
Latest Posts
Latest Posts
-
A Cinema Seats 280 People Of 98
Jun 08, 2025
-
In The Fourth Paragraph The Narrator Presents Himself As
Jun 08, 2025
-
Which Expression Is Equivalent To 4 7i 3 4i
Jun 08, 2025
-
Which Statement Most Accurately Describes Confucianism
Jun 08, 2025
-
3 01 Quiz Participial And Absolute Phrases
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Solve This Inequality 3q 11 8q 99 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.