Solve Y Ax2 C For X
Breaking News Today
Jun 07, 2025 · 5 min read
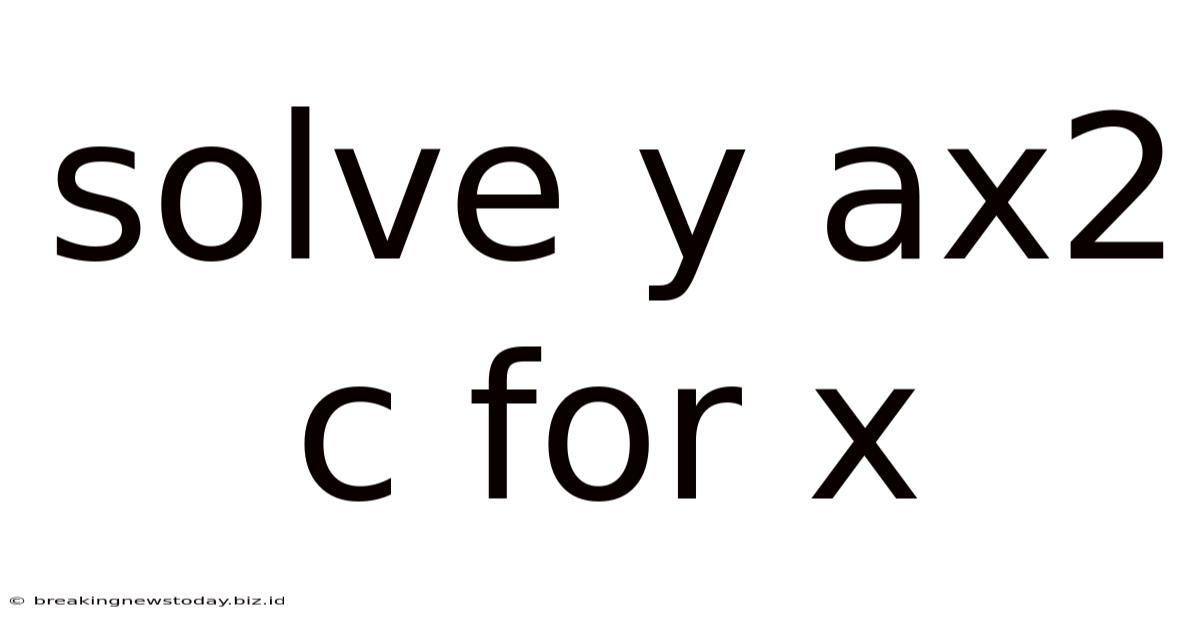
Table of Contents
Solving for x: A Comprehensive Guide to y = ax² + c
Solving quadratic equations is a fundamental skill in algebra with wide-ranging applications in various fields, from physics and engineering to finance and computer science. This comprehensive guide delves into the intricacies of solving for x in the equation y = ax² + c, equipping you with the knowledge and techniques to tackle such problems confidently. We'll explore different approaches, provide step-by-step examples, and discuss the significance of understanding the underlying mathematical concepts.
Understanding the Equation: y = ax² + c
The equation y = ax² + c represents a parabola, a symmetrical U-shaped curve. Let's break down the components:
- y: Represents the dependent variable, the output or result of the equation. It's the vertical position on the graph.
- x: Represents the independent variable, the input value. It's the horizontal position on the graph.
- a: Represents the vertical scaling factor. It determines how wide or narrow the parabola is. A larger absolute value of a results in a narrower parabola, while a smaller absolute value results in a wider parabola. The sign of a determines whether the parabola opens upwards (a > 0) or downwards (a < 0).
- c: Represents the y-intercept, the point where the parabola intersects the y-axis (where x = 0). It's the vertical shift of the parabola.
Methods for Solving y = ax² + c for x
Unlike simpler linear equations, solving for x in a quadratic equation like y = ax² + c requires a different approach. Here are the key methods:
1. Isolating x² and Taking the Square Root
This method is the most straightforward approach when dealing with the basic form of the equation, y = ax² + c. The steps are as follows:
- Isolate the x² term: Subtract c from both sides of the equation:
y - c = ax² - Solve for x²: Divide both sides by a:
(y - c) / a = x² - Take the square root: Take the square root of both sides:
±√[(y - c) / a] = x
Important Note: Remember to consider both the positive and negative square roots, as both will satisfy the equation. This leads to two possible solutions for x, unless (y-c)/a is equal to zero.
Example: Solve for x in the equation y = 2x² + 5, when y = 15.
- 15 - 5 = 2x²
- 10 / 2 = x²
- x² = 5
- x = ±√5
Therefore, the solutions are x = √5 and x = -√5.
2. Using the Quadratic Formula (for more complex scenarios)
While the above method works well for the simple form y = ax² + c, the quadratic formula provides a more general solution for quadratic equations of the form ax² + bx + c = 0. In our case, b = 0.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Since b = 0 in our equation, the formula simplifies to:
x = ±√(-c/a)
This is essentially the same result as the previous method, but the quadratic formula offers a more robust approach that can handle more complex quadratic equations where a bx term is present.
Example: Let's re-solve the previous example using the quadratic formula: y = 2x² + 5, when y = 15.
- Rearrange the equation to the standard form: 2x² - 10 = 0
- Apply the quadratic formula with a = 2, b = 0, and c = -10: x = [0 ± √(0² - 4 * 2 * -10)] / (2 * 2) x = ±√(80) / 4 x = ±√(16*5) / 4 x = ±4√5 / 4 x = ±√5
Again, the solutions are x = √5 and x = -√5.
Interpreting the Solutions and Graphing the Parabola
The solutions for x represent the points where the parabola intersects a horizontal line at a given y-value. Consider the following:
- No Real Solutions: If (y - c) / a is negative, there are no real solutions. This means the horizontal line at the given y-value does not intersect the parabola.
- One Real Solution: If (y - c) / a is zero, there is only one real solution (x = 0). This occurs at the vertex of the parabola.
- Two Real Solutions: If (y - c) / a is positive, there are two real solutions, representing the two points where the horizontal line intersects the parabola.
Graphing the parabola can help visualize these solutions. The vertex of the parabola, which is the lowest (if a > 0) or highest (if a < 0) point, is located at (0, c). Plotting a few points and sketching the curve will clarify the relationship between the y-value and the corresponding x-values.
Applications of Solving y = ax² + c
Solving quadratic equations of this form has numerous practical applications across diverse fields:
- Physics: Calculating projectile motion, determining the trajectory of an object under the influence of gravity.
- Engineering: Designing parabolic antennas, optimizing structures for strength and stability.
- Finance: Modeling investment growth, calculating compound interest.
- Computer Graphics: Creating curves and shapes, generating realistic animations.
- Statistics: Analyzing data distributions, fitting curves to experimental results.
Advanced Concepts and Extensions
The equation y = ax² + c serves as a foundation for understanding more complex quadratic equations. Here are some advanced concepts to explore:
- Quadratic Equations with a 'bx' term: Equations of the form ax² + bx + c = 0 require the use of the quadratic formula or factoring techniques.
- Complex Solutions: In some cases, the discriminant (b² - 4ac) in the quadratic formula can be negative, leading to complex solutions involving imaginary numbers.
- Solving Systems of Quadratic Equations: Problems may involve solving multiple quadratic equations simultaneously.
Conclusion
Mastering the ability to solve for x in the equation y = ax² + c is a crucial step in developing a strong foundation in algebra. By understanding the methods presented here – isolating x², utilizing the quadratic formula, and interpreting the solutions graphically – you can confidently tackle a wide range of problems in mathematics and its various applications. Remember to always check your work and consider the practical implications of your solutions within the context of the problem. Further exploration into advanced quadratic concepts will build upon this foundation, expanding your mathematical capabilities even further.
Latest Posts
Latest Posts
-
Which Statement Best Describes The Theme Of Song Of Myself
Jun 07, 2025
-
Which Best Describes The Use Of Irony In This Excerpt
Jun 07, 2025
-
All Of The Following Are True About Clep Except
Jun 07, 2025
-
Creating A Venn Diagram Takes Specialized Computer Software
Jun 07, 2025
-
A Patient Is Suffering From The Inability To Distinguish
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Solve Y Ax2 C For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.