The Expression Above Can Also Be Written In The Form
Breaking News Today
Mar 31, 2025 · 5 min read
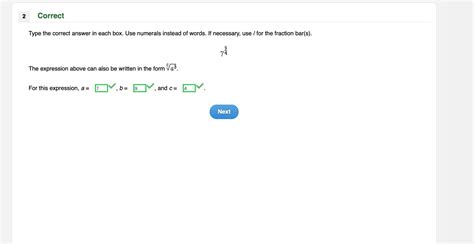
Table of Contents
The Expression Above Can Also Be Written In The Form: Exploring Mathematical Equivalence and Transformations
Mathematical expressions, like sentences in a language, can often be expressed in multiple ways while retaining the same meaning. Understanding these different forms is crucial for solving problems, simplifying complex equations, and gaining a deeper understanding of mathematical concepts. This article delves into the various methods of transforming mathematical expressions, emphasizing the importance of equivalence and exploring numerous examples across different mathematical areas.
What Does "The Expression Above Can Also Be Written In The Form" Mean?
This phrase signifies that a given mathematical expression can be rewritten in an equivalent but potentially simpler or more useful form. This transformation doesn't change the fundamental value of the expression; it merely alters its appearance. The goal of such transformations is often to:
- Simplify the expression: Make it easier to understand and work with.
- Solve an equation: Rearrange the expression to isolate a variable.
- Reveal underlying structure: Uncover hidden patterns or relationships.
- Prepare for further calculations: Put the expression into a form suitable for a specific technique or theorem.
The techniques used depend heavily on the type of expression (algebraic, trigonometric, logarithmic, etc.) and the desired outcome.
Transforming Algebraic Expressions
Algebraic expressions involve variables, constants, and arithmetic operations. Transformations here often involve applying properties like the distributive property, combining like terms, and factoring.
1. Distributive Property: This property states that a(b + c) = ab + ac. This allows us to expand or factor expressions.
- Example: The expression 3(x + 2) can also be written in the form 3x + 6. Here, we've used the distributive property to expand the expression. Conversely, 3x + 6 can be written in the factored form 3(x + 2).
2. Combining Like Terms: Terms with the same variables raised to the same powers can be combined.
- Example: The expression 2x + 5y + 3x - 2y can also be written in the simplified form 5x + 3y. We've combined the 'x' terms and the 'y' terms separately.
3. Factoring: This involves expressing an expression as a product of simpler expressions. Common factoring techniques include factoring out the greatest common factor (GCF) and factoring quadratic expressions.
- Example: The expression x² + 5x + 6 can also be written in the factored form (x + 2)(x + 3). This is achieved by finding two numbers that add up to 5 (the coefficient of x) and multiply to 6 (the constant term).
4. Completing the Square: This technique is particularly useful for solving quadratic equations and transforming quadratic expressions into vertex form.
- Example: The expression x² + 6x + 5 can be written in the form (x + 3)² - 4 by completing the square. This reveals the vertex of the parabola represented by the quadratic expression.
Transforming Trigonometric Expressions
Trigonometric expressions involve trigonometric functions like sine, cosine, and tangent. Transformations often utilize trigonometric identities to simplify or rewrite expressions.
1. Pythagorean Identities: These identities relate the squares of sine, cosine, and tangent. For instance, sin²θ + cos²θ = 1.
- Example: The expression 1 - cos²θ can also be written in the form sin²θ using the Pythagorean identity.
2. Sum-to-Product and Product-to-Sum Identities: These identities allow us to rewrite sums or products of trigonometric functions into different forms.
- Example: The expression sin x + sin y can be rewritten using the sum-to-product identity as 2sin((x+y)/2)cos((x-y)/2).
3. Double and Half-Angle Identities: These identities relate trigonometric functions of double or half angles to functions of the original angle.
- Example: The expression 2sinθcosθ can also be written in the form sin(2θ) using the double-angle identity for sine.
Transforming Logarithmic and Exponential Expressions
Logarithmic and exponential expressions are closely related through the inverse relationship between logarithms and exponents. Transformations often involve applying logarithm properties or exponent rules.
1. Logarithm Properties: These properties govern how logarithms handle products, quotients, and exponents. For example, log(ab) = log a + log b.
- Example: The expression log(100x) can also be written in the form log 100 + log x = 2 + log x.
2. Exponent Rules: These rules dictate how exponents behave with multiplication, division, and exponentiation. For example, aᵐaⁿ = aᵐ⁺ⁿ.
- Example: The expression 2³ * 2² can also be written in the form 2⁵.
3. Change of Base Formula: This formula allows us to change the base of a logarithm.
- Example: log₂8 can be rewritten using the change of base formula as (log₁₀ 8) / (log₁₀ 2).
The Importance of Equivalent Forms
The ability to rewrite a mathematical expression in different forms is fundamental to mathematical proficiency. It allows us to:
- Solve equations: Many solution methods require the equation to be in a specific form.
- Simplify calculations: Simpler expressions are often easier to evaluate or manipulate.
- Understand relationships: Different forms can highlight different aspects of the expression.
- Apply theorems and formulas: Many mathematical theorems and formulas require expressions to be in a particular form before they can be applied.
- Improve problem-solving strategies: Recognizing equivalent forms can open up new avenues for problem-solving.
Examples Across Different Mathematical Fields
The concept of rewriting expressions extends far beyond basic algebra. Here are some more advanced examples:
- Calculus: Rewriting functions in different forms is crucial for differentiation and integration. For instance, partial fraction decomposition simplifies the integration of rational functions.
- Linear Algebra: Matrix operations often involve transforming matrices into equivalent forms, such as row-echelon form or diagonal form.
- Differential Equations: Transformations like Laplace transforms are used to solve differential equations by converting them into simpler algebraic equations.
- Complex Analysis: Complex numbers are often expressed in different forms (rectangular, polar, exponential) depending on the context.
Conclusion
The statement "the expression above can also be written in the form..." is a cornerstone of mathematical manipulation. Mastering the art of transforming mathematical expressions is not just about algebraic dexterity; it's about developing a deeper understanding of mathematical relationships, unveiling hidden structures, and ultimately, becoming a more effective problem-solver. The ability to recognize and utilize equivalent forms unlocks a wider range of solution strategies and fosters a more intuitive grasp of the underlying mathematical principles. Continuous practice and exploration of diverse mathematical concepts are essential for developing this crucial skill.
Latest Posts
Latest Posts
-
Plasterers Scaffolds Horse Scaffolds And Window Jacks
Apr 01, 2025
-
Motor Vehicle Crashes Cost American Taxpayers Over
Apr 01, 2025
-
What Is The Difference Between A Load And A Control
Apr 01, 2025
-
Paper Based Pii Is Involved In Data Breaches More Often
Apr 01, 2025
-
Breaking Down Information For Quick Repetition And Memorization Means Using
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about The Expression Above Can Also Be Written In The Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
