The Hanger Image Below Represents A Balanced Equation.
Breaking News Today
Jun 04, 2025 · 5 min read
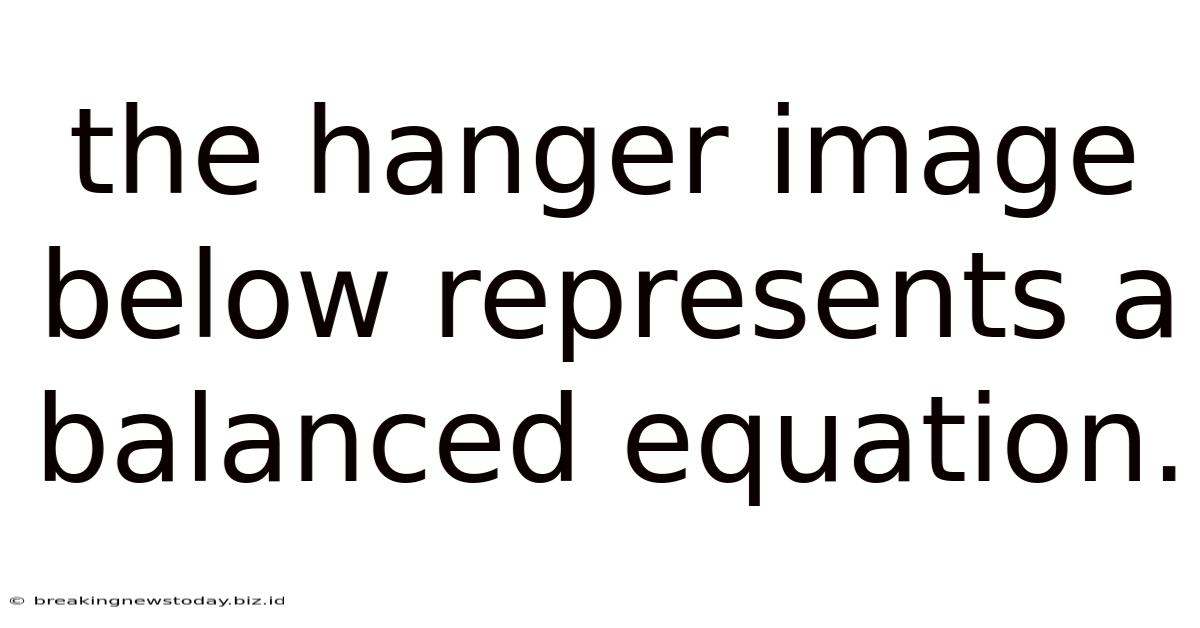
Table of Contents
Decoding the Hanger: A Visual Representation of Balanced Equations
The humble clothes hanger, a fixture in most closets, can surprisingly serve as a powerful tool for understanding mathematical concepts. Specifically, the image of a hanger with weights on either side perfectly illustrates the fundamental principle of balanced equations. This article delves deep into this visual representation, exploring its implications for understanding algebra, problem-solving, and even the broader concept of equilibrium in various fields. We'll unravel the visual metaphor and translate it into concrete mathematical principles, making the abstract world of equations more accessible and intuitive.
The Hanger Analogy: A Simple yet Powerful Tool
Imagine a clothes hanger suspended from a central point, perfectly balanced. Now, picture weights hung on either side. For the hanger to remain balanced, the total weight on the left side must equal the total weight on the right side. This seemingly simple scenario elegantly captures the essence of a balanced equation.
The hanger's fulcrum (the central point of suspension) represents the equals sign (=) in an equation. The weights on either side represent the expressions on each side of the equals sign. Maintaining balance signifies that the expressions on both sides of the equation are equal in value. This visual representation makes the abstract concept of equality remarkably concrete and easy to grasp, especially for beginners.
Key elements of the hanger analogy:
- Fulcrum: Represents the equals sign (=).
- Left side weights: Represent the expression on the left side of the equation.
- Right side weights: Represent the expression on the right side of the equation.
- Balance: Indicates that the equation is true – the expressions on both sides are equal.
From Hanger to Equation: Translating the Visual
Let's translate this visual metaphor into mathematical terms. Consider a simple equation: x + 2 = 5. Using the hanger analogy:
- The fulcrum: The central point of the hanger represents the equals sign (=).
- Left side:
x + 2is represented by a weight labeled 'x' and another weight labeled '2' on the left side of the hanger. - Right side:
5is represented by a weight labeled '5' on the right side of the hanger.
For the hanger (and therefore the equation) to be balanced, the total weight on the left side must equal the total weight on the right side. This allows us to solve for 'x'. To maintain balance, we need to remove a weight of '2' from both sides. This is equivalent to subtracting '2' from both sides of the equation:
x + 2 - 2 = 5 - 2
This simplifies to:
x = 3
The hanger now shows a weight of '3' on the left side, perfectly balanced by the weight of '5' on the right side (after the removal of the '2' weight from both sides). We have successfully solved for 'x'.
Applying the Hanger Analogy to Complex Equations
The power of the hanger analogy lies in its ability to simplify even complex algebraic equations. Consider a slightly more intricate example: 2x + 4 = x + 7.
- Left side: We have two weights labeled 'x' and a weight labeled '4'.
- Right side: We have a weight labeled 'x' and a weight labeled '7'.
To solve this equation visually, we can strategically remove weights from both sides to maintain balance. Let's start by removing a weight labeled 'x' from both sides:
This leaves us with:
x + 4 = 7
Now, we remove a weight of '4' from both sides:
x = 3
Again, the hanger (and the equation) remains balanced, demonstrating the solution x = 3.
Extending the Analogy: Inequalities and More
While the hanger analogy primarily illustrates balanced equations, it can also provide insights into inequalities. If the weights on one side are heavier, the hanger tilts, reflecting the inequality. This visual representation can help students understand the concept of "greater than" (>) and "less than" (<) in a tangible way.
Furthermore, the hanger analogy's flexibility extends beyond basic algebraic equations. It can be adapted to demonstrate concepts like:
- Combining like terms: Visualize combining weights of the same value.
- Distributive property: Illustrate how distributing weights affects the overall balance.
- Solving systems of equations: Imagine multiple hangers representing multiple equations, requiring adjustments across all to achieve simultaneous balance.
The Pedagogical Power of Visual Aids
The use of visual aids like the hanger analogy in mathematics education is invaluable. Abstract concepts often become much clearer when presented visually. This is particularly important for students who struggle with abstract reasoning. The hanger analogy provides a concrete, hands-on approach to learning, encouraging active participation and deeper understanding.
Furthermore, the hanger analogy caters to various learning styles. Visual learners benefit directly from the visual representation, while kinesthetic learners can create their own physical models using actual hangers and weights. This multi-sensory approach enhances engagement and memory retention.
Beyond Mathematics: Applications in Other Fields
The concept of balance represented by the hanger analogy extends far beyond the realm of mathematics. It finds applications in various fields, including:
- Physics: Concepts like equilibrium, forces, and levers are fundamentally about balance, echoing the principles of balanced equations.
- Engineering: Structural engineers rely on the principles of balance to ensure the stability and safety of buildings and other structures.
- Chemistry: Chemical reactions often involve balancing equations to ensure the conservation of mass.
- Economics: Economic models frequently involve balancing supply and demand to reach an equilibrium point.
Conclusion: The Enduring Relevance of the Hanger
The seemingly simple image of a balanced hanger provides a powerful and versatile tool for understanding mathematical concepts and extending those concepts into other fields. Its visual simplicity transforms the abstract into the concrete, making complex ideas more accessible and intuitive, particularly for students at all levels. The hanger analogy is a testament to the power of visual aids in education and their enduring relevance in simplifying and explaining intricate concepts in various disciplines. Its enduring usefulness speaks to the fact that sometimes, the most effective teaching tools are those that are surprisingly simple and readily available. The next time you encounter a balanced equation, remember the humble clothes hanger—a potent symbol of mathematical equilibrium and a testament to the power of visual representation in learning. By understanding this simple analogy, we can gain a deeper appreciation for the elegance and logic inherent within the world of mathematics and beyond.
Latest Posts
Latest Posts
-
Composers Choose Instrument Combinations When Orchestrating A Piece
Jun 06, 2025
-
0 001 Is 1 10 Of What Number
Jun 06, 2025
-
Use The Bootstrap Distributions In Figure 1
Jun 06, 2025
-
A Ship Sails At 15 Miles Per Hour
Jun 06, 2025
-
Which Of The Following Statements Describes Data Interoperability
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about The Hanger Image Below Represents A Balanced Equation. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.