The Positive Number A Is 2241 Of The Sum
Breaking News Today
Jun 02, 2025 · 5 min read
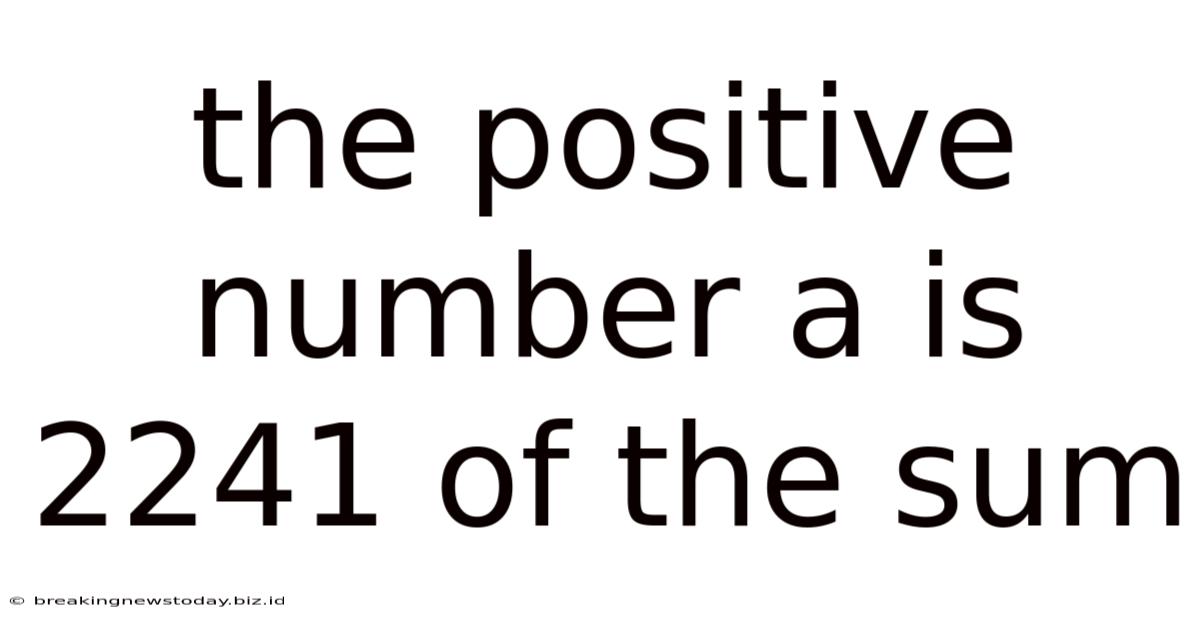
Table of Contents
Unlocking the Mysteries of Positive Number 'a': When 'a' is 2241/x of the Sum
The seemingly simple statement, "the positive number 'a' is 2241/x of the sum," opens a door to a fascinating exploration of mathematical relationships and problem-solving strategies. Understanding this statement requires us to delve into the world of fractions, ratios, proportions, and algebraic manipulation. This article will unpack this statement, exploring various scenarios and providing practical examples to illustrate the concepts involved. We'll also touch upon the significance of this type of problem in various fields, highlighting its relevance beyond theoretical mathematics.
Understanding the Core Concept: Fractions and Ratios
At its heart, the statement "the positive number 'a' is 2241/x of the sum" describes a proportional relationship. The fraction 2241/x represents a ratio, comparing the value of 'a' to the overall sum. To grasp this, let's break down the key elements:
-
Positive Number 'a': This is the unknown quantity we aim to find or understand better. Its positivity is a crucial constraint, limiting our solution set.
-
2241: This is a constant numerator, providing a fixed reference point in the ratio.
-
x: This is a variable denominator, which introduces flexibility and allows for exploring different scenarios. The value of 'x' significantly influences the value of 'a'.
-
Of the Sum: This phrase indicates that the number 'a' is a part of a larger sum. This sum can be composed of multiple numbers, including 'a' itself. Defining the components of this sum is critical to solving any specific problem.
Different Interpretations and Scenarios
The ambiguity in the statement allows for multiple interpretations, depending on the context of the "sum." Let's examine a few potential scenarios:
Scenario 1: 'a' is part of a two-number sum
Imagine 'a' and 'b' are two positive numbers, and their sum is 'S' (S = a + b). The statement then becomes:
a = (2241/x) * (a + b)
This equation has two unknowns ('a' and 'b'). To solve for 'a', we need additional information, such as the value of 'b' or the relationship between 'a' and 'b'. For instance, if we know that b = 2a, we can substitute this into the equation and solve for 'a'.
Scenario 2: 'a' is part of a multi-number sum
Let's consider a sum consisting of 'n' positive numbers, including 'a'. Let the sum of these 'n' numbers be 'S'. The statement then translates to:
a = (2241/x) * S
Again, this equation requires additional information to solve for 'a'. We need to know the values of the other (n-1) numbers and the value of 'x'. Solving this requires setting up a system of equations or relying on further information about the relationship between 'a' and the other numbers in the sum.
Scenario 3: 'a' as a fraction of a specific known sum
Suppose the sum 'S' is a known constant, say 10000. Then the equation becomes:
a = (2241/x) * 10000
In this case, solving for 'a' depends solely on the value of 'x'. Different values of 'x' will yield different values for 'a'. For example:
- If x = 1, then a = 22410000
- If x = 2241, then a = 10000
- If x = 10000, then a = 2241
This demonstrates the direct relationship between 'x' and 'a' when the sum is known.
Applying Algebraic Techniques
Solving for 'a' in the general case requires algebraic manipulation. The complexity of the solution will depend on the nature of the sum and the relationships between 'a' and other numbers involved. Here's a general approach:
-
Define the sum: Clearly define the sum (S) in terms of 'a' and other variables.
-
Substitute into the equation: Substitute the expression for the sum into the equation a = (2241/x) * S.
-
Solve for 'a': Use algebraic techniques (e.g., simplification, factoring, solving linear or quadratic equations) to isolate 'a' and express it in terms of the other variables and constants.
-
Check the solution: Ensure that the solution for 'a' is positive, as specified in the problem statement. Also, verify that the solution makes logical sense within the context of the problem.
Real-World Applications
Problems involving proportional relationships and ratios, like the one posed, appear frequently in various fields:
-
Finance: Calculating interest, determining profit margins, and analyzing investment returns often involve proportional relationships.
-
Engineering: Scaling designs, calculating material requirements, and analyzing stress and strain necessitate an understanding of ratios and proportions.
-
Chemistry: Stoichiometric calculations in chemical reactions heavily rely on ratios between reactants and products.
-
Statistics: Many statistical calculations and analyses, including proportions and percentages, rely on similar principles.
-
Computer Science: Algorithms involving data structures and scaling often involve proportional relationships.
Expanding on the Problem: Introducing Constraints
Let's enhance the problem by introducing additional constraints to make it more challenging and realistic:
Problem: The positive number 'a' is 2241/x of the sum of itself and another positive number 'b'. The sum of 'a' and 'b' is less than 10,000. If x = 7, find the possible values of 'a' and 'b'.
Solution:
-
Formulate the equation: The problem translates to: a = (2241/7) * (a + b), which simplifies to a = 320.14(a + b).
-
Simplify: We get a = 320.14a + 320.14b. Rearranging, we have 319.14a = -320.14b.
-
Solve for 'a' in terms of 'b': a = (-320.14b) / 319.14 ≈ -1.0031b
Since 'a' and 'b' are positive numbers, this equation reveals an inconsistency. There's no solution that satisfies both the given equation and the constraint that 'a' and 'b' are positive. This highlights the importance of carefully analyzing the constraints of a problem before attempting a solution. The inherent contradiction in the problem statement is a key takeaway.
Conclusion: The Importance of Context and Critical Thinking
The statement "the positive number 'a' is 2241/x of the sum" is not a self-contained problem; it's a framework for a multitude of problems. The key to solving such problems lies in carefully understanding the context, defining the sum, and applying appropriate algebraic techniques. Crucially, we must always check our solutions for consistency and realism, paying close attention to the constraints imposed by the problem statement. This exploration underscores the importance of not just mathematical skills, but also critical thinking and analytical reasoning in solving mathematical problems. The seemingly simple mathematical statement leads us on a journey that demands careful interpretation, strategic problem-solving, and a robust understanding of mathematical concepts. This type of problem-solving is transferable to numerous fields, emphasizing its practical value and relevance beyond the purely academic.
Latest Posts
Latest Posts
-
What Is Z In The Figure Above
Jun 04, 2025
-
Which Context Describes A Difference Of Rational Numbers
Jun 04, 2025
-
Having Heard This Line In The Prologue The Audience Can
Jun 04, 2025
-
You Are Describing The Boot Process To A Friend
Jun 04, 2025
-
If A Reclamation Facility Receives A Tank
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about The Positive Number A Is 2241 Of The Sum . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.