The Sampling Distribution Of A Sample Mean Refers To
Breaking News Today
Apr 03, 2025 · 7 min read
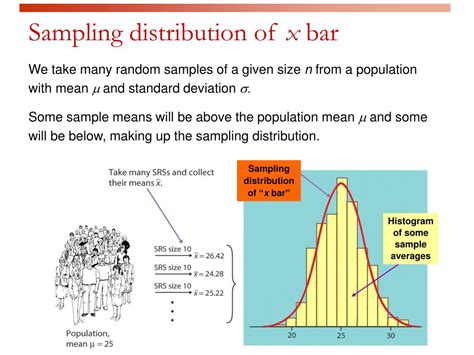
Table of Contents
The Sampling Distribution of a Sample Mean: A Comprehensive Guide
Understanding the sampling distribution of the sample mean is crucial for anyone working with statistical inference. It bridges the gap between a sample statistic (like the sample mean) and the population parameter it estimates (the population mean). This article will delve deep into this concept, explaining its properties, importance, and applications. We'll explore the Central Limit Theorem, its assumptions, and its profound implications for statistical hypothesis testing and confidence intervals.
What is the Sampling Distribution of the Sample Mean?
The sampling distribution of the sample mean is the probability distribution of all possible sample means of a given sample size drawn from a population. Instead of focusing on individual data points, we focus on the distribution of the averages of many samples. Imagine taking numerous random samples from a population, calculating the mean for each sample, and then plotting those means. This plot represents the sampling distribution.
It's crucial to distinguish between the population distribution, which describes the distribution of the entire population, and the sampling distribution, which describes the distribution of sample means. The sampling distribution is not the same as the population distribution; it provides information about the variability of sample means.
Why is the Sampling Distribution Important?
The sampling distribution is fundamental to statistical inference because it allows us to make inferences about a population based on sample data. We often don't have access to the entire population, so we rely on samples to estimate population parameters. The sampling distribution quantifies the uncertainty associated with these estimates.
Specifically, the sampling distribution helps us:
-
Estimate the population mean: The mean of the sampling distribution is an unbiased estimator of the population mean. This means, on average, the sample means will be centered around the true population mean.
-
Determine the precision of our estimates: The standard deviation of the sampling distribution (called the standard error) measures the variability of sample means. A smaller standard error indicates that our sample means are clustered closely around the population mean, implying more precise estimates.
-
Construct confidence intervals: We use the sampling distribution to build confidence intervals, which provide a range of plausible values for the population mean.
-
Conduct hypothesis testing: We use the sampling distribution to assess the probability of observing a sample mean as extreme as the one obtained, given a certain hypothesis about the population mean.
The Central Limit Theorem: The Cornerstone of Sampling Distributions
The Central Limit Theorem (CLT) is a cornerstone of statistics. It states that, under certain conditions, the sampling distribution of the sample mean approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution. This is incredibly powerful because it allows us to use the well-understood properties of the normal distribution to make inferences, even if the population distribution is unknown or non-normal.
Conditions for the Central Limit Theorem
While the CLT is remarkably robust, certain conditions must be met for it to hold:
-
Independence: The samples must be independent of each other. This means that the selection of one sample point does not influence the selection of any other sample point. This is often achieved through random sampling.
-
Random Sampling: Samples must be drawn randomly from the population. This ensures that every member of the population has an equal chance of being selected.
-
Sample Size: The sample size needs to be sufficiently large. While there's no universally agreed-upon minimum sample size, a general rule of thumb is a sample size of at least 30. However, for highly skewed populations, a larger sample size might be necessary.
Implications of the Central Limit Theorem
The implications of the CLT are profound:
-
Normalization: Even if the population distribution is skewed or non-normal, the sampling distribution of the sample mean will be approximately normal for large sample sizes. This simplifies statistical calculations and inferences significantly.
-
Standard Error: The standard error of the mean (SEM) is the standard deviation of the sampling distribution. It is calculated as the population standard deviation divided by the square root of the sample size: SEM = σ/√n, where σ is the population standard deviation and n is the sample size. If the population standard deviation is unknown (which is usually the case), the sample standard deviation (s) is used as an estimate.
-
Confidence Intervals: The CLT allows us to construct confidence intervals around the sample mean, providing a range of values within which the population mean is likely to fall with a certain level of confidence (e.g., 95%).
-
Hypothesis Testing: The CLT forms the basis of many hypothesis tests, allowing us to determine whether the observed sample mean is significantly different from a hypothesized population mean.
Illustrative Example: Understanding the Sampling Distribution in Action
Let's consider a scenario: Suppose we are interested in the average height of adult women in a specific country. The population is vast, making it impractical to measure the height of every woman. Instead, we take several random samples of, say, 50 women each, measure their heights, and calculate the mean height for each sample.
We'll then have a set of sample means. The distribution of these sample means constitutes the sampling distribution of the sample mean. Due to the Central Limit Theorem, even if the population distribution of heights isn't perfectly normal (it might be slightly skewed), the distribution of the sample means will be approximately normal, especially with a sample size of 50.
The mean of this sampling distribution will be a good estimate of the true average height of adult women in that country. The standard deviation of the sampling distribution (the standard error) tells us how much the sample means vary. A smaller standard error indicates more precise estimation of the population mean.
Applications of the Sampling Distribution of the Sample Mean
The sampling distribution of the sample mean has widespread applications across various fields, including:
-
Quality Control: In manufacturing, sampling distributions are used to monitor the quality of products. By taking samples and calculating the mean of a certain characteristic (e.g., weight, length), manufacturers can determine if the production process is stable and meets quality standards.
-
Public Opinion Polls: Polling organizations use sampling distributions to estimate the proportion of the population holding a particular opinion. By randomly sampling a smaller group, they can infer the overall opinion of the larger population with a margin of error, reflecting the uncertainty inherent in sampling.
-
Medical Research: In clinical trials, sampling distributions are crucial for assessing the effectiveness of new treatments. By comparing the treatment and control groups' sample means, researchers can determine if the treatment has a statistically significant effect.
-
Finance: In financial modeling, sampling distributions are used to simulate the returns of investments and assess the risk associated with different portfolios.
Beyond the Mean: Sampling Distributions of Other Statistics
While this article focuses on the sampling distribution of the sample mean, it's important to note that sampling distributions can be constructed for other sample statistics as well, such as:
-
Sample Variance: The sampling distribution of the sample variance describes the variability of sample variances around the population variance.
-
Sample Proportion: The sampling distribution of the sample proportion is used to make inferences about population proportions, often encountered in opinion polls and surveys.
-
Sample Median: The sampling distribution of the sample median provides an alternative to the sample mean, particularly useful for data with outliers.
Understanding these different sampling distributions is critical for choosing the appropriate statistical methods in different contexts.
Conclusion
The sampling distribution of the sample mean is a fundamental concept in statistics, providing a bridge between sample data and population parameters. The Central Limit Theorem underpins its importance, guaranteeing approximate normality of the sampling distribution under certain conditions. This knowledge is essential for constructing confidence intervals, conducting hypothesis tests, and making reliable inferences about populations based on sample data across a wide range of disciplines. Mastering this concept is key to a solid understanding of statistical inference and its powerful applications.
Latest Posts
Latest Posts
-
Turnabouts And Railroad Crossings Are Examples Of
Apr 04, 2025
-
Ap Classroom Unit 3 Progress Check Mcq Answers
Apr 04, 2025
-
Assuming No Air Resistance All Projectiles Have
Apr 04, 2025
-
How Can You Uncover Your Buyer Personas Reading Habits
Apr 04, 2025
-
Financial Accounting Is Often Referred To As A
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about The Sampling Distribution Of A Sample Mean Refers To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
