The Sum Of 21 And 4 Doubled
Breaking News Today
Jun 08, 2025 · 5 min read
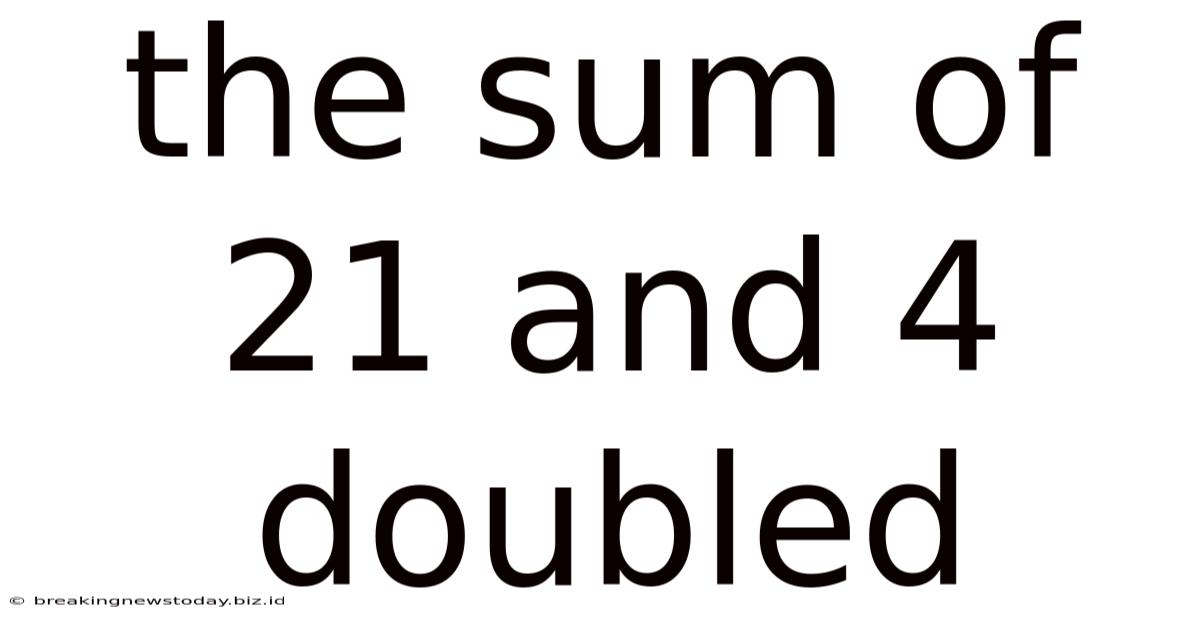
Table of Contents
The Sum of 21 and 4, Doubled: A Deep Dive into Basic Arithmetic and its Applications
This seemingly simple mathematical problem – finding the double of the sum of 21 and 4 – offers a surprising springboard for exploring fundamental arithmetic concepts, their real-world applications, and even their historical significance. While the answer itself is straightforward (40, of course!), the journey to understand its implications is far more enriching. Let's delve in.
Understanding the Problem: A Step-by-Step Approach
The problem statement "The sum of 21 and 4, doubled" can be broken down into easily manageable steps:
Step 1: Finding the Sum
The first step involves calculating the sum of 21 and 4. This is a simple addition problem:
21 + 4 = 25
Step 2: Doubling the Sum
The second step involves doubling the sum obtained in Step 1. This means multiplying the sum by 2:
25 x 2 = 50
Therefore, the final answer is 50.
Beyond the Basics: Exploring Mathematical Concepts
While the solution is readily apparent, this simple problem provides an excellent opportunity to explore fundamental mathematical concepts:
1. The Commutative Property of Addition
The commutative property states that the order of numbers in an addition problem doesn't affect the result. In this case, we could have added 4 and 21 instead of 21 and 4, and the sum would still be 25:
4 + 21 = 25
This seemingly minor detail underscores an important principle underlying arithmetic operations.
2. The Associative Property of Addition
The associative property states that when adding multiple numbers, the grouping of numbers doesn't affect the result. While not directly applicable to the simple addition of two numbers in this problem, it becomes relevant when dealing with more complex sums. For instance, consider adding 21, 4, and 6:
(21 + 4) + 6 = 25 + 6 = 31 21 + (4 + 6) = 21 + 10 = 31
The result remains the same regardless of how the numbers are grouped.
3. The Distributive Property
The distributive property links addition and multiplication. It states that multiplying a sum by a number is the same as multiplying each addend by the number and then adding the products. While not explicitly used in the solution, it's relevant in understanding how multiplication and addition interact:
2 x (21 + 4) = (2 x 21) + (2 x 4) = 42 + 8 = 50
This property is crucial in simplifying algebraic expressions and solving more complex equations.
4. Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), dictates the sequence in which operations should be performed. In this problem, the parentheses (or brackets) are implicit. We must first perform the addition within the implied brackets before performing the multiplication (doubling):
(21 + 4) x 2 = 25 x 2 = 50
This seemingly simple rule is essential for avoiding ambiguity and ensuring accurate calculations in more complex mathematical problems.
Real-World Applications: Beyond the Textbook
The seemingly basic arithmetic underlying this problem has countless real-world applications:
1. Everyday Budgeting and Finance
Calculating the total cost of items and then doubling it to account for a potential discount or tax is a frequent application of this type of arithmetic. Imagine buying two identical items: the total cost is calculated by adding the individual price of each item and then doubling it.
2. Measurement and Conversions
Doubling the sum of two lengths or quantities is commonly used in various fields. For instance, doubling the sum of two distances could be needed in construction or engineering calculations.
3. Recipe Scaling
Many recipes call for doubling or halving ingredients. If a recipe requires 21 grams of flour and 4 grams of baking powder, doubling the recipe will involve doubling the sum of these quantities.
4. Inventory Management
In businesses that handle multiple items, calculating the total value of inventory and doubling it to account for potential future orders is crucial.
5. Geometry and Area Calculations
While less directly linked, the principles of addition and multiplication are central to calculating areas of complex shapes. Breaking down the shapes into simpler components and calculating areas using addition and multiplication is a vital aspect of many geometry problems.
Historical Context: A Glimpse into Mathematical History
The fundamental arithmetic operations used in this problem – addition and multiplication – have a rich history. Their development played a crucial role in the advancement of mathematics and its application in various fields.
Ancient civilizations, like the Egyptians and Babylonians, used sophisticated methods for addition and multiplication, albeit with different notations and approaches. The development of the decimal system significantly streamlined arithmetic operations, making calculations much more efficient. The concept of zero and its incorporation into the number system proved revolutionary.
The understanding and application of these basic arithmetic operations laid the groundwork for more advanced mathematical concepts such as algebra, calculus, and even modern computing.
Conclusion: The Power of Simple Arithmetic
The seemingly simple problem of doubling the sum of 21 and 4 offers a surprisingly rich avenue for exploration. It reinforces the importance of fundamental arithmetic concepts, demonstrates their wide-ranging applicability in various fields, and provides a glimpse into the fascinating history of mathematics. By breaking down this simple problem, we can appreciate the power of basic arithmetic and its enduring relevance in our lives. While the answer is a simple 50, the journey of understanding the underlying principles and applications reveals a much deeper mathematical significance. This simple calculation is not just about numbers; it’s about the foundation of quantitative reasoning and its indispensable role in understanding and shaping our world.
Latest Posts
Latest Posts
-
Exercise 2 Context Clues Column A Answer Key
Jun 08, 2025
-
5 Hundreds X 10 In Unit Form
Jun 08, 2025
-
All Of The Following Are Characteristics Of Professional Behavior Except
Jun 08, 2025
-
Which Type Of Water Is Generally Preferred For Shampooing
Jun 08, 2025
-
Which Of The Following Correctly Describes A Security Patch
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of 21 And 4 Doubled . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.