Twice A Number K Plus The Quantity S Minus 2
Breaking News Today
Jun 02, 2025 · 5 min read
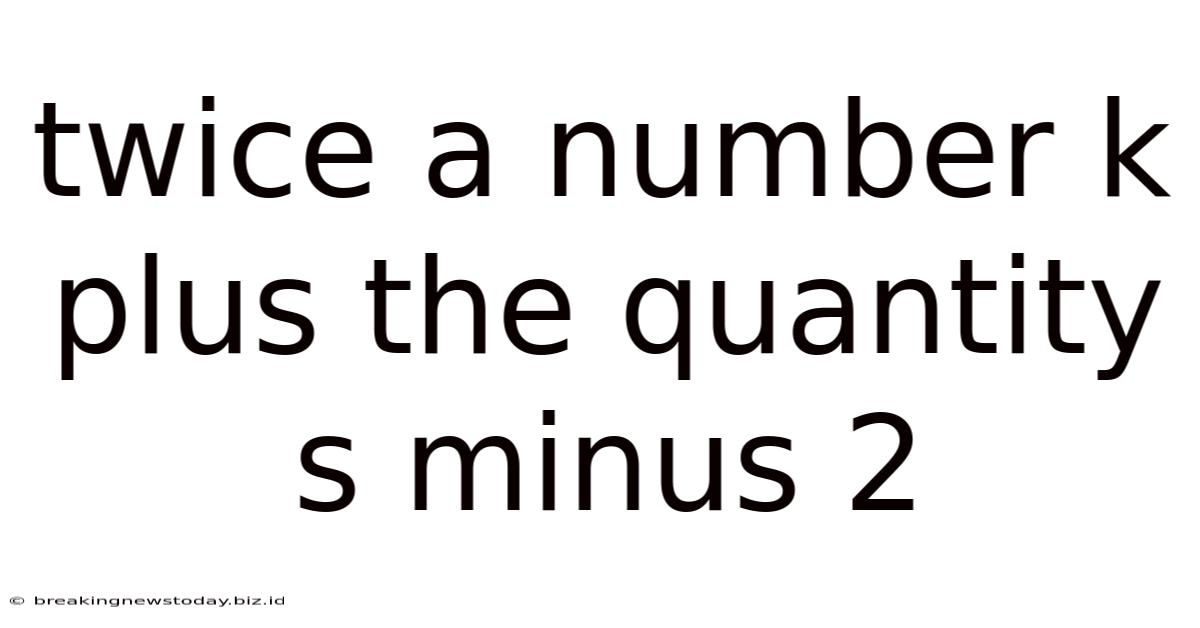
Table of Contents
Twice a Number K Plus the Quantity S Minus 2: A Deep Dive into Mathematical Expressions
This article will delve into the mathematical expression "twice a number k plus the quantity s minus 2," exploring its various interpretations, applications, and the importance of understanding algebraic notation. We'll cover translating words into algebraic expressions, simplifying expressions, solving equations involving this expression, and even exploring real-world scenarios where this type of expression might be useful.
Understanding the Expression
The expression "twice a number k plus the quantity s minus 2" can be broken down into its constituent parts to fully grasp its meaning. Let's dissect it step-by-step:
- A number k: This represents an unknown variable, denoted by the letter 'k'. It can represent any numerical value.
- Twice a number k: This translates to 2k, meaning the number k multiplied by 2.
- The quantity s minus 2: This signifies the expression (s - 2), implying that 2 is subtracted from the variable s. The parentheses are crucial; they indicate that the subtraction should be performed before any other operation.
- Plus: This indicates addition.
Therefore, the complete algebraic expression is: 2k + (s - 2). Note that the parentheses are vital for maintaining the correct order of operations. Without them, the expression would be interpreted differently, leading to an incorrect result.
Translating Words into Algebra: A Crucial Skill
The ability to translate written descriptions into algebraic expressions is a fundamental skill in mathematics and beyond. It's the bridge between real-world problems and the tools we use to solve them. Understanding this process allows us to model various scenarios using mathematical equations. This example, "twice a number k plus the quantity s minus 2," perfectly illustrates this translation. Let's practice with a few more examples:
- Three times a number x minus five: This translates to 3x - 5.
- The sum of y and z divided by 4: This translates to (y + z) / 4.
- The square of a number m added to seven: This translates to m² + 7.
The key is to carefully break down the sentence, identifying each operation (addition, subtraction, multiplication, division) and the variables or constants involved. Practice is key to mastering this important skill.
Simplifying the Expression
While the expression 2k + (s - 2) is perfectly valid, it can be simplified. The parentheses are unnecessary in this case because addition has lower precedence than subtraction. Applying the distributive property doesn't change the expression's value, but it makes it more concise. Therefore, we can simplify the expression to:
2k + s - 2
This simplified form is equivalent to the original expression and is generally preferred for its conciseness. This highlights the importance of understanding algebraic manipulation techniques for optimizing mathematical expressions.
Solving Equations Involving the Expression
Let's consider scenarios where our expression, 2k + s - 2, forms part of an equation. We'll need additional information to solve for k and s. For example:
Scenario 1: 2k + s - 2 = 10
To solve this equation, we need additional information. We have two unknowns (k and s) and only one equation. We can't find unique solutions for k and s without another equation relating them. Let's assume we know that k = 3. Substituting this into the equation, we get:
2(3) + s - 2 = 10
6 + s - 2 = 10
s + 4 = 10
s = 6
Therefore, if k = 3, then s = 6 satisfies the equation.
Scenario 2: Let's say we have another equation: k + s = 7. We can now use a system of equations to solve for k and s.
We have the system:
- 2k + s - 2 = 10
- k + s = 7
We can solve this system using substitution or elimination. Let's use substitution. From equation 2, we can express s as s = 7 - k. Substituting this into equation 1:
2k + (7 - k) - 2 = 10
2k + 7 - k - 2 = 10
k + 5 = 10
k = 5
Now, substituting k = 5 back into equation 2:
5 + s = 7
s = 2
Thus, the solution to the system of equations is k = 5 and s = 2.
Real-World Applications
Although this might seem like an abstract mathematical exercise, expressions like "twice a number k plus the quantity s minus 2" have real-world applications in various fields. Consider these examples:
- Geometry: Calculating the perimeter of a rectangle with sides of length k and (s-2) units, where k is twice the length of (s-2) would directly use this concept.
- Finance: Modeling investment returns, where k represents an initial investment, s represents gains from a second investment, and you are factoring in a 2-unit fee.
- Physics: Describing the motion of an object where k represents initial velocity and s represents acceleration over a period of 2 seconds.
The possibilities are vast. The core concept of combining variables and constants through mathematical operations is fundamental to numerous fields requiring quantitative analysis.
Expanding the Concept: More Complex Expressions
The basic expression can be expanded to include more variables, operations, and even exponents. For example:
- 3(2k + (s - 2))²: This introduces squaring and multiplication, increasing the complexity of the calculation but building upon the foundational understanding of the simpler expression.
- 2k + (s - 2) + m/n: This introduces fractions, further expanding the range of problems that can be modeled.
Mastering the simpler expressions is crucial before tackling more complex ones. The ability to handle algebraic manipulations, including order of operations (PEMDAS/BODMAS), is essential for accurately interpreting and solving these more involved expressions.
Conclusion: The Power of Algebraic Expressions
The seemingly simple expression "twice a number k plus the quantity s minus 2" offers a gateway into the wider world of algebra. It underscores the importance of accurately translating words into mathematical symbols, simplifying expressions, and solving equations. Through this example, we've explored the fundamental building blocks of algebra and shown its relevance across various disciplines. By mastering the manipulation and interpretation of algebraic expressions, we equip ourselves with powerful tools for solving problems and modeling real-world scenarios with accuracy and efficiency. The key to success lies in consistent practice and a thorough understanding of fundamental algebraic principles. Remember, every complex equation is built upon simpler components, just like this seemingly straightforward example.
Latest Posts
Latest Posts
-
Which Bar Graph Best Represents The Provided Data
Jun 04, 2025
-
Lady Capulet Doubts Benvolios Description Of The Fight Because
Jun 04, 2025
-
For Your Job You Often Fly Between Seattle And Miami
Jun 04, 2025
-
Human Movement Involves The Complex Interplay Of Many Body Systems
Jun 04, 2025
-
Driving With Headlights On Reduces The Chance Of Collisions By
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about Twice A Number K Plus The Quantity S Minus 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.