Two Fifths The Cube Of A Number
Breaking News Today
Jun 07, 2025 · 5 min read
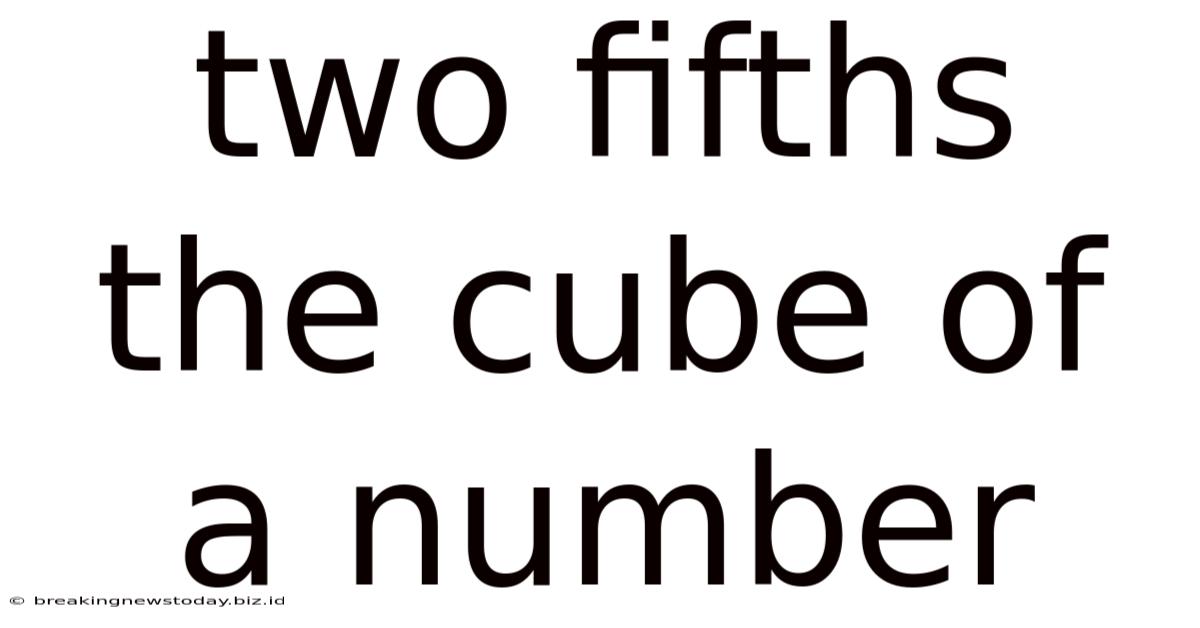
Table of Contents
Two Fifths the Cube of a Number: A Deep Dive into Mathematical Exploration
This article delves into the mathematical expression "two fifths the cube of a number," exploring its various interpretations, applications, and implications within different mathematical contexts. We'll move beyond the simple calculation and examine the underlying concepts, providing a comprehensive understanding suitable for students, educators, and anyone with a curious mind.
Understanding the Core Expression
The phrase "two fifths the cube of a number" translates directly into a mathematical expression. Let's break it down:
- A number: We'll represent this unknown number with the variable x.
- The cube of a number: This means raising the number to the power of 3, resulting in x³.
- Two fifths: This represents the fraction 2/5.
Therefore, the complete mathematical expression is: (2/5)x³ or equivalently, *(2/5)x³ or 2x³/5. This expression forms the bedrock of our exploration.
Exploring Different Mathematical Contexts
This seemingly simple expression can be explored across various mathematical branches, including algebra, calculus, and even geometry. Let's examine some of these applications:
1. Algebraic Manipulation
Algebraic manipulation involves simplifying, expanding, or solving equations containing this expression. For example:
-
Solving for x: If we're given the equation (2/5)x³ = 8, we can solve for x using algebraic techniques. First, multiply both sides by 5/2: x³ = 20. Then, taking the cube root of both sides gives us x = ³√20.
-
Expanding expressions: Consider an expression like 2( (2/5)x³ + 4). This can be expanded using the distributive property: (4/5)x³ + 8.
-
Factoring expressions: More complex scenarios might involve factoring expressions containing (2/5)x³. This requires a deep understanding of factoring techniques and might involve the use of greatest common factors or other advanced methods.
2. Calculus Applications
In calculus, this expression can be used within the context of:
-
Derivatives: Finding the derivative of (2/5)x³ with respect to x is a straightforward application of the power rule of differentiation: d/dx [(2/5)x³] = (6/5)x². This derivative represents the instantaneous rate of change of the function at any given point.
-
Integrals: The indefinite integral of (2/5)x³ is calculated using the power rule of integration: ∫(2/5)x³ dx = (1/10)x⁴ + C, where C is the constant of integration. This represents the family of functions whose derivative is (2/5)x³. Definite integrals would involve calculating the area under the curve of the function within specified limits.
-
Optimization problems: In optimization problems, we might need to find the maximum or minimum value of a function involving this expression. This frequently involves utilizing derivatives and setting them to zero to find critical points.
3. Geometric Interpretations
While not directly obvious, there are geometric interpretations related to this expression:
-
Volume of a cube: x³ represents the volume of a cube with side length x. Therefore, (2/5)x³ could represent a fraction (two-fifths) of the volume of this cube.
-
Scaling and transformations: We can visualize this expression as a transformation of a cube, where the volume is scaled by a factor of 2/5. This involves shrinking or expanding the cube's dimensions proportionally.
Real-World Applications
Beyond the theoretical realm, "two fifths the cube of a number" can find its place in real-world scenarios:
-
Engineering and Physics: In various engineering and physics problems involving volume calculations, scaling, or rate of change, this expression might emerge. For example, it could represent the volume of a specific section of a structure or a portion of a fluid flow.
-
Data Analysis and Statistics: Statistical models might utilize this type of expression within their formulas. This is especially relevant when dealing with cubic relationships between variables.
-
Financial Modeling: While less direct, cubic relationships (and their fractional components) can appear in complex financial models, especially when modeling growth or decay over time.
Advanced Considerations
Let's delve into more complex aspects related to the expression:
1. Complex Numbers
If x is allowed to be a complex number (a number involving the imaginary unit i, where i² = -1), then the cube of x and consequently (2/5)x³ will also be complex. This opens up a whole new level of mathematical exploration involving complex number arithmetic and geometric representations on the complex plane.
2. Series and Sequences
This expression can be incorporated into series and sequences. For example, consider a series where each term is given by (2/5)n³, where 'n' represents the term number. Analyzing the convergence or divergence of such a series requires advanced mathematical techniques.
3. Differential Equations
Differential equations often incorporate functions and their derivatives. Equations involving (2/5)x³ or its derivatives might arise in modelling various physical phenomena, requiring specialized solution methods.
Conclusion: Beyond the Basics
While seemingly simple, the expression "two fifths the cube of a number" offers a rich landscape for mathematical exploration. From basic algebraic manipulations to advanced calculus applications and complex number theory, its potential extends far beyond simple calculations. This comprehensive analysis highlights the multifaceted nature of even seemingly elementary mathematical concepts and demonstrates their relevance across various fields. By understanding this expression's properties and applications, we gain a deeper appreciation for the power and elegance of mathematics. The seemingly straightforward expression is a gateway to more complex and sophisticated mathematical concepts, reminding us that the foundation of mathematics is the key to unlocking advanced applications. Furthermore, this exploration encourages a more inquisitive approach to mathematical problem-solving, encouraging a deeper understanding and appreciation of the subject.
Latest Posts
Latest Posts
-
A Recent Study Compared The Vaccination Histories Of 256
Jun 07, 2025
-
Graph X 2 9 On A Number Line
Jun 07, 2025
-
Which Piecewise Function Is Shown On The Graph
Jun 07, 2025
-
Caroline Bought 20 Shares Of Stock
Jun 07, 2025
-
If M Lmp Is 11 Degrees More Than
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Two Fifths The Cube Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.