Two Thirds A Number Plus 4 Is 7
Breaking News Today
Jun 03, 2025 · 4 min read
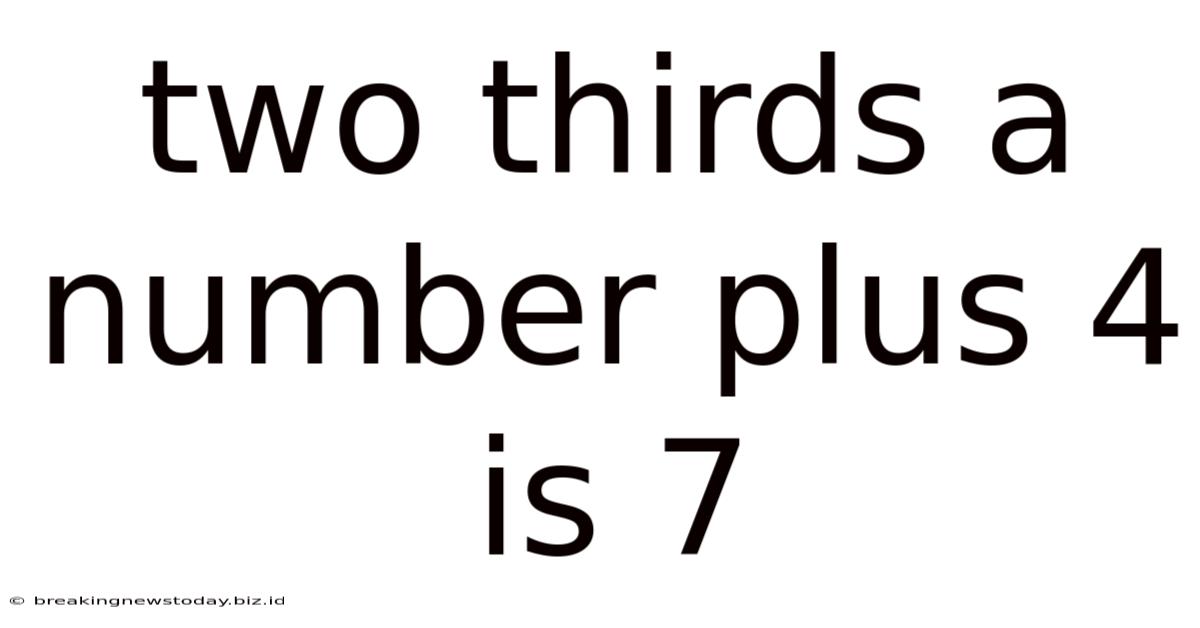
Table of Contents
Two Thirds of a Number Plus 4 is 7: Solving Algebraic Equations
This seemingly simple equation, "two thirds of a number plus 4 is 7," is a fantastic gateway into the world of algebra. It introduces fundamental concepts like variables, coefficients, and solving for unknowns – skills crucial for anyone navigating higher-level mathematics, science, and even everyday problem-solving. This comprehensive guide will dissect this equation, explore various solution methods, and then expand upon the core concepts to build a stronger foundation in algebra.
Understanding the Problem: Deconstructing the Equation
Let's break down the sentence into its mathematical components:
-
"Two thirds of a number": This translates to (2/3)x, where 'x' represents the unknown number. The fraction 2/3 acts as the coefficient of the variable.
-
"Plus 4": This is a simple addition operation, adding 4 to the previous term.
-
"is 7": This indicates equality; the entire expression equals 7.
Combining these elements, we arrive at the algebraic equation:
(2/3)x + 4 = 7
Method 1: Solving Using Inverse Operations
This is the most straightforward approach. We aim to isolate the variable 'x' by performing inverse operations, one step at a time. Remember, whatever operation you perform on one side of the equation must be performed on the other side to maintain balance.
-
Subtract 4 from both sides: This reverses the addition of 4.
(2/3)x + 4 - 4 = 7 - 4
(2/3)x = 3
-
Multiply both sides by 3/2: This is the inverse of multiplying by 2/3. Multiplying by the reciprocal cancels out the fraction.
(3/2) * (2/3)x = 3 * (3/2)
x = 9/2 or x = 4.5
Therefore, the unknown number is 4.5.
Verifying the Solution
It's always a good practice to check your answer. Substitute x = 4.5 back into the original equation:
(2/3)(4.5) + 4 = 3 + 4 = 7
The equation holds true, confirming our solution.
Method 2: Solving Using a Common Denominator
This method is particularly useful when dealing with fractions. We can eliminate the fraction by finding a common denominator and then solving.
-
Find a common denominator: In this case, the denominator is 3. We can rewrite 4 as 12/3.
(2/3)x + 12/3 = 7
-
Rewrite 7 as a fraction with the common denominator: We rewrite 7 as 21/3.
(2/3)x + 12/3 = 21/3
-
Combine the fractions: Since they share a common denominator, we can combine the terms on the left-hand side.
(2x + 12)/3 = 21/3
-
Eliminate the denominator: Multiply both sides of the equation by 3.
2x + 12 = 21
-
Solve for x: Subtract 12 from both sides and then divide by 2.
2x = 9
x = 9/2 = 4.5
This method yields the same solution as the previous one, x = 4.5.
Expanding on Algebraic Concepts
The simple equation we've solved provides a springboard to understanding more complex algebraic concepts. Let's explore some of them:
Variables and Constants
-
Variables: These are represented by letters (like 'x' in our equation) and represent unknown quantities. Their value can change.
-
Constants: These are fixed numerical values (like 4 and 7 in our equation). Their value remains constant.
Coefficients
The coefficient is the numerical factor of a term. In our equation, (2/3) is the coefficient of the variable x. It indicates the scaling or multiplying factor applied to the variable.
Linear Equations
Our equation is a linear equation because the highest power of the variable 'x' is 1. Linear equations are always represented by a straight line when graphed.
Solving Equations with Multiple Variables
While our equation had only one variable, many equations involve multiple variables. To solve these, you'll often need a system of equations with the same number of equations as variables. Methods like substitution and elimination are used to find the values of each variable.
Solving Equations with Higher Powers
Equations where the highest power of the variable is greater than 1 (e.g., x², x³) are non-linear equations and require different solution techniques, such as factoring, the quadratic formula (for quadratic equations), or numerical methods.
Real-World Applications of Algebra
Algebra isn't confined to textbooks; it's a powerful tool with numerous real-world applications:
-
Finance: Calculating interest, loan repayments, and investments.
-
Engineering: Designing structures, circuits, and systems.
-
Physics: Modeling motion, forces, and energy.
-
Computer Science: Developing algorithms and software.
-
Data Analysis: Interpreting data trends and making predictions.
Practice Problems
To solidify your understanding, try solving these similar problems:
-
One-third of a number plus 5 is 9. Find the number.
-
Two-fifths of a number minus 3 is 7. Find the number.
-
Three-quarters of a number added to 2 is 11. Find the number.
Conclusion: Mastering the Fundamentals
The equation "(2/3)x + 4 = 7" may appear simple at first glance, but it serves as a robust introduction to the fundamental principles of algebra. Understanding how to solve this equation and the underlying concepts – variables, coefficients, inverse operations – lays a solid foundation for tackling more advanced mathematical problems. Consistent practice and exploration of related concepts are key to mastering algebra and unlocking its potential in diverse fields. Remember to always verify your solutions and don't hesitate to explore different solution methods to deepen your understanding.
Latest Posts
Latest Posts
-
Order The Eclipses By Increasing Brightness Of The Moon
Jun 05, 2025
-
Which Quotation From The Passage Best States Reagans Message
Jun 05, 2025
-
What Design Feature Of The Hagia Sophia Was Considered Daring
Jun 05, 2025
-
What Additional Information Does The Sidebar Provide
Jun 05, 2025
-
What Does Each Stanza In Auspex Show
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about Two Thirds A Number Plus 4 Is 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.