Use The Gcf To Factor 24+6x
Breaking News Today
Jun 08, 2025 · 6 min read
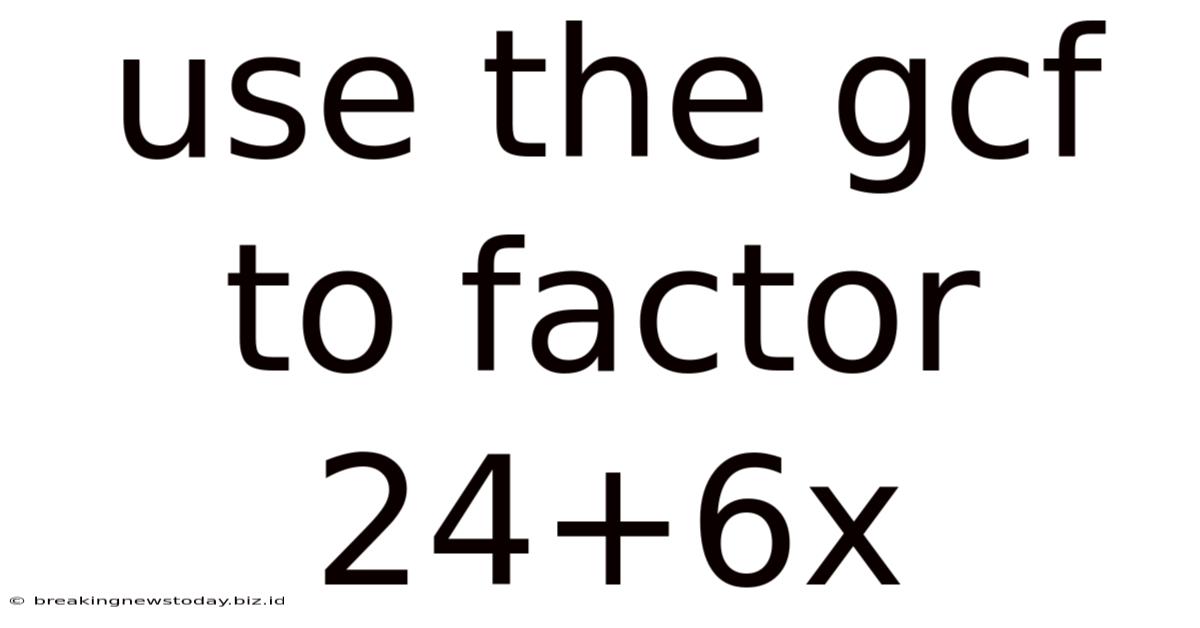
Table of Contents
Using the GCF to Factor 24 + 6x: A Comprehensive Guide
Factoring algebraic expressions is a fundamental skill in algebra. Understanding how to factor expressions efficiently is crucial for solving equations, simplifying expressions, and progressing to more advanced algebraic concepts. One of the simplest yet most important factoring techniques involves using the Greatest Common Factor (GCF). This article delves into the process of factoring the expression 24 + 6x using the GCF, explaining the underlying principles and providing a step-by-step approach, along with examples to solidify your understanding. We'll also explore the broader context of GCF factoring and its applications.
What is the Greatest Common Factor (GCF)?
Before we tackle factoring 24 + 6x, let's define the GCF. The GCF of a set of numbers or terms is the largest number or expression that divides each of them without leaving a remainder. Finding the GCF is the first step in many factoring problems. It simplifies the expression and makes further factoring (if needed) easier. To find the GCF, you typically consider the prime factorization of each number or term.
Example: Let's find the GCF of 12 and 18.
- The prime factorization of 12 is 2 x 2 x 3 (or 2² x 3).
- The prime factorization of 18 is 2 x 3 x 3 (or 2 x 3²).
The common factors are 2 and 3. The greatest common factor is 2 x 3 = 6.
Factoring 24 + 6x using the GCF
Now, let's apply this knowledge to factor the expression 24 + 6x. The key is to identify the GCF of the terms 24 and 6x.
Step 1: Find the GCF of the coefficients
The coefficients are 24 and 6. We already know from the previous example that the GCF of 24 and 6 is 6.
Step 2: Find the GCF of the variables
The variable in the expression is x. The first term, 24, doesn't have an 'x', but the second term, 6x, does. Therefore, the GCF of the variables is simply 1 (as x¹ divides x¹ and x⁰).
Step 3: Combine the GCFs
The GCF of 24 and 6x is the product of the GCFs of the coefficients and the variables. In this case, it's 6 x 1 = 6.
Step 4: Factor out the GCF
Now, we factor out the GCF (6) from each term of the expression:
24 + 6x = 6(4) + 6(x)
Notice that we divide each term by the GCF (6): 24/6 = 4 and 6x/6 = x.
Step 5: Write the factored form
Finally, we rewrite the expression in its factored form by writing the GCF outside the parentheses and the remaining terms inside the parentheses:
24 + 6x = 6(4 + x)
Therefore, the factored form of 24 + 6x is 6(4 + x). This is the simplest factored form using the GCF.
Verifying the Factored Form
It's always a good practice to verify your factored form by expanding it. If you expand 6(4 + x), you should get back the original expression:
6(4 + x) = 6 * 4 + 6 * x = 24 + 6x
Since we obtained the original expression, we can confidently say that our factoring is correct.
Advanced Examples and Applications of GCF Factoring
While 24 + 6x is a relatively simple example, the GCF factoring technique can be applied to more complex algebraic expressions. Let's explore a few examples:
Example 1: Factoring 15x² + 25x
- Find the GCF of coefficients: The GCF of 15 and 25 is 5.
- Find the GCF of variables: Both terms contain 'x', and the lowest power of x is x¹. Therefore, the GCF of variables is x.
- Combine GCFs: The overall GCF is 5x.
- Factor out the GCF: 15x² + 25x = 5x(3x) + 5x(5) = 5x(3x + 5)
Therefore, the factored form is 5x(3x + 5).
Example 2: Factoring 12a²b³ + 18a³b²
- Find the GCF of coefficients: The GCF of 12 and 18 is 6.
- Find the GCF of variables: The lowest power of 'a' is a², and the lowest power of 'b' is b². Therefore, the GCF of variables is a²b².
- Combine GCFs: The overall GCF is 6a²b².
- Factor out the GCF: 12a²b³ + 18a³b² = 6a²b²(2b) + 6a²b²(3a) = 6a²b²(2b + 3a)
Therefore, the factored form is 6a²b²(2b + 3a).
Example 3: Factoring expressions with negative coefficients
When dealing with negative coefficients, the process remains the same, but be mindful of the signs.
Factor -12x - 18y
- GCF of coefficients: The GCF of -12 and -18 is 6. Note, it's positive 6 because we're factoring it out.
- GCF of variables: There is no common variable.
- Factor out the GCF: -12x - 18y = 6(-2x) + 6(-3y) = 6(-2x -3y)
The factored form is 6(-2x - 3y)
Applications of GCF Factoring in Real-World Problems
GCF factoring isn't just an abstract mathematical concept; it has practical applications in various fields:
- Geometry: Calculating the area of composite shapes often involves factoring.
- Physics: Simplifying equations in physics problems often utilizes GCF factoring.
- Engineering: In structural design or circuit analysis, simplifying complex expressions might necessitate GCF factoring.
- Finance: Calculating compound interest or analyzing investment returns might use simplified expressions obtained through factoring.
Beyond GCF Factoring: Other Factoring Techniques
While GCF factoring is a foundational technique, other methods exist for factoring more complex polynomials:
- Difference of Squares: This technique applies to expressions of the form a² - b².
- Trinomial Factoring: This method is used for factoring quadratic trinomials (expressions of the form ax² + bx + c).
- Grouping: This technique is helpful when factoring polynomials with four or more terms.
Mastering GCF factoring is crucial before moving on to these more advanced techniques. It forms the groundwork for understanding and applying more sophisticated algebraic concepts.
Conclusion
Factoring algebraic expressions is a vital skill in algebra, and understanding the Greatest Common Factor (GCF) is the cornerstone of many factoring methods. This article provides a comprehensive guide to factoring expressions using the GCF, demonstrating the process step-by-step and showcasing examples ranging from simple expressions like 24 + 6x to more complex ones involving multiple variables and negative coefficients. Remember to always verify your factored form by expanding it to ensure accuracy. With practice and a solid understanding of the principles involved, you'll confidently navigate the world of algebraic factoring and successfully apply this skill to various mathematical and real-world problems. By mastering GCF factoring, you lay a robust foundation for tackling more advanced algebraic concepts and their applications.
Latest Posts
Latest Posts
-
Gina Wilson All Things Algebra Probability And Statistics Answer Key
Jun 08, 2025
-
How Many Times Does 2 Go Into 72
Jun 08, 2025
-
Political Leaders May Prefer Communicating Through Social Media Because
Jun 08, 2025
-
What Are The Coordinates Of Point K
Jun 08, 2025
-
It Networking Involves Which Of These Choose All That Apply
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Use The Gcf To Factor 24+6x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.