Use The Gcf To Factor 8x+16 .
Breaking News Today
Jun 04, 2025 · 5 min read
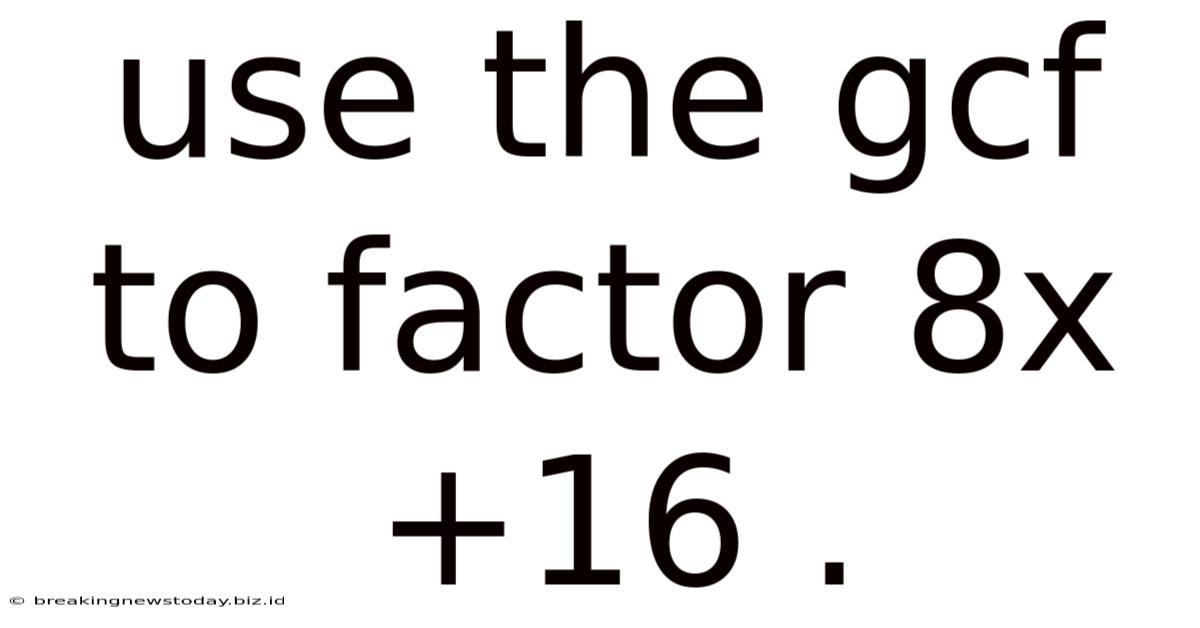
Table of Contents
Using the GCF to Factor 8x + 16: A Comprehensive Guide
Factoring algebraic expressions is a fundamental skill in algebra. It's the process of breaking down an expression into simpler components, much like finding the prime factors of a number. One of the most common and essential factoring techniques involves using the Greatest Common Factor (GCF). This article will delve deep into understanding and applying the GCF to factor expressions, using the example of 8x + 16 as our primary focus. We'll explore the concept thoroughly, providing numerous examples and clarifying common misconceptions.
Understanding the Greatest Common Factor (GCF)
Before tackling the factoring of 8x + 16, let's solidify our understanding of the GCF. The GCF of two or more numbers (or terms in an algebraic expression) is the largest number (or term) that divides evenly into all of them. Finding the GCF is crucial in simplifying expressions and solving equations.
How to Find the GCF:
There are several methods to determine the GCF:
-
Listing Factors: List all the factors of each number, and then identify the largest factor common to all.
For example, let's find the GCF of 12 and 18:
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 18: 1, 2, 3, 6, 9, 18
The common factors are 1, 2, 3, and 6. The greatest common factor is 6.
-
Prime Factorization: Break down each number into its prime factors. The GCF is the product of the common prime factors raised to the lowest power.
For example, let's find the GCF of 24 and 36:
24 = 2³ × 3 36 = 2² × 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2², and the lowest power of 3 is 3¹. Therefore, the GCF is 2² × 3 = 12.
-
Euclidean Algorithm (for two numbers): This method is particularly efficient for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's find the GCF of 48 and 18:
48 = 2 × 18 + 12 18 = 1 × 12 + 6 12 = 2 × 6 + 0
The last non-zero remainder is 6, so the GCF of 48 and 18 is 6.
Factoring 8x + 16 using the GCF
Now, let's apply our understanding of the GCF to factor the expression 8x + 16.
Step 1: Find the GCF of the coefficients.
The coefficients are 8 and 16. Let's find their GCF using any of the methods described above. Using prime factorization:
8 = 2³ 16 = 2⁴
The common prime factor is 2, and the lowest power is 2³. Therefore, the GCF of 8 and 16 is 8.
Step 2: Find the GCF of the variables (if any).
In the expression 8x + 16, only the first term contains a variable (x). Therefore, there is no common variable factor.
Step 3: Factor out the GCF.
Since the GCF of 8 and 16 is 8, we factor out 8 from the expression:
8x + 16 = 8(x + 2)
Verification:
To verify our factoring, we can expand the factored expression:
8(x + 2) = 8x + 16
This matches the original expression, confirming that our factoring is correct.
More Examples of Factoring using GCF
Let's solidify our understanding with more examples:
Example 1: Factor 12y² + 18y
- GCF of coefficients: The GCF of 12 and 18 is 6.
- GCF of variables: The common variable is y, and the lowest power is y¹.
- Factoring: 12y² + 18y = 6y(2y + 3)
Example 2: Factor 5a³ - 15a² + 20a
- GCF of coefficients: The GCF of 5, 15, and 20 is 5.
- GCF of variables: The common variable is a, and the lowest power is a¹.
- Factoring: 5a³ - 15a² + 20a = 5a(a² - 3a + 4)
Example 3: Factor -4b² + 8b - 12
- GCF of coefficients: The GCF of -4, 8, and -12 is -4 (It's good practice to factor out the negative sign if the leading coefficient is negative).
- GCF of variables: The common variable is b, and the lowest power is b¹.
- Factoring: -4b² + 8b - 12 = -4(b² - 2b + 3)
Common Mistakes to Avoid
-
Incomplete Factoring: Make sure you've factored out the greatest common factor. For example, factoring 12x + 18 as 2(6x + 9) is incorrect because 6 is still a common factor. The correct factoring is 6(2x + 3).
-
Incorrect Signs: Pay close attention to signs when factoring out a negative GCF. Remember that multiplying a negative by a negative results in a positive.
-
Forgetting the GCF: Always check if a GCF exists before attempting other factoring methods. Factoring out the GCF simplifies the expression, making further factoring easier (if necessary).
Advanced Applications of GCF Factoring
GCF factoring is not just limited to simple binomial expressions like 8x + 16. It plays a crucial role in various algebraic manipulations:
-
Simplifying Fractions: GCF factoring is essential for simplifying rational expressions (fractions with algebraic expressions). By factoring the numerator and denominator, you can often cancel out common factors, simplifying the expression significantly.
-
Solving Equations: Factoring, including using the GCF, is frequently used in solving quadratic equations and other polynomial equations.
-
Finding Roots and Zeros: The factored form of a polynomial makes it easier to find its roots (the values of the variable that make the expression equal to zero).
Conclusion
Understanding and effectively applying the greatest common factor (GCF) is a cornerstone of algebraic manipulation. It's a fundamental skill that underpins more advanced factoring techniques and is crucial for simplifying expressions, solving equations, and working with rational expressions. Mastering GCF factoring, as demonstrated through examples like 8x + 16, provides a solid foundation for success in algebra and beyond. Remember to always check your work and look for opportunities to simplify your results. Practice regularly, and soon you'll be factoring expressions with ease and confidence.
Latest Posts
Latest Posts
-
Parallel Lines J And K Are Cut By Transversal T
Jun 06, 2025
-
What Electrical Hazard Is Present In This Image
Jun 06, 2025
-
Affections In Baroque Usage Refers To
Jun 06, 2025
-
For Lateral And Component Conversions Career Waypoints
Jun 06, 2025
-
An Example Of Hyper Organization Is
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Use The Gcf To Factor 8x+16 . . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.