What Is 1 7 Of 28
Breaking News Today
Jun 05, 2025 · 5 min read
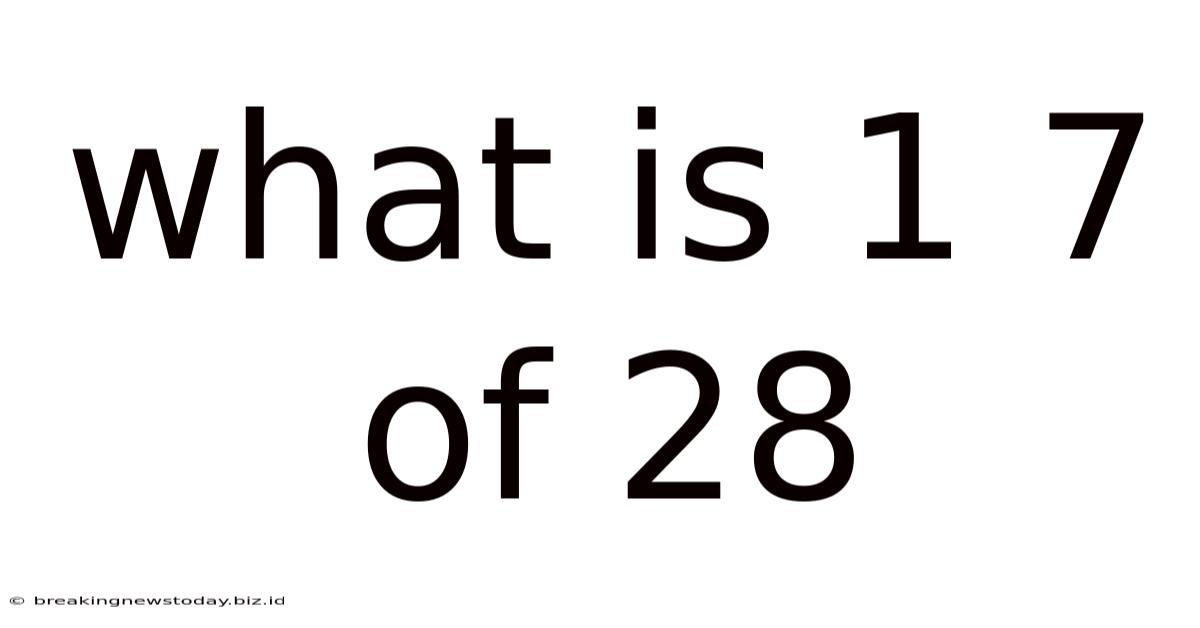
Table of Contents
What is 1/7 of 28? A Comprehensive Guide to Fractions and Their Applications
Finding a fraction of a number is a fundamental concept in mathematics with broad applications in various fields. This article delves deep into the question "What is 1/7 of 28?" We'll not only solve this specific problem but also explore the underlying principles of fractions, different methods of calculation, and real-world examples to solidify your understanding. By the end, you'll be confident in tackling similar problems and applying fractional concepts to diverse situations.
Understanding Fractions: A Quick Refresher
Before diving into the calculation, let's revisit the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 1/7, 1 is the numerator and 7 is the denominator. This means we're considering one part out of a total of seven equal parts.
Calculating 1/7 of 28: Method 1 - Direct Multiplication
The most straightforward method to find a fraction of a number is to multiply the fraction by the number. In this case:
(1/7) * 28
To perform this multiplication, we can follow these steps:
- Multiply the numerator by the whole number: 1 * 28 = 28
- Divide the result by the denominator: 28 / 7 = 4
Therefore, 1/7 of 28 is 4.
Calculating 1/7 of 28: Method 2 - Division First
Alternatively, we can approach this problem by first dividing the whole number by the denominator of the fraction and then multiplying by the numerator. This method can be particularly helpful when dealing with larger numbers or more complex fractions.
- Divide the whole number by the denominator: 28 / 7 = 4
- Multiply the result by the numerator: 4 * 1 = 4
Again, we arrive at the answer: 1/7 of 28 is 4.
Visualizing the Problem
Let's visualize this problem to reinforce our understanding. Imagine you have 28 identical objects, such as apples. To find 1/7 of 28, you would divide the 28 apples into 7 equal groups. Each group would contain 4 apples. Therefore, 1/7 of the total (28 apples) is 4 apples.
Real-World Applications of Fractions
The concept of finding a fraction of a number is ubiquitous in daily life. Here are some examples:
- Cooking: A recipe might call for 2/3 of a cup of flour. This requires understanding fractions to accurately measure ingredients.
- Shopping: Sales often advertise discounts as fractions, such as "1/4 off" or "2/5 off." Knowing how to calculate fractions is essential for determining the final price.
- Sharing: Dividing a pizza or cake among friends involves understanding fractions to ensure fair portions.
- Measurement: Many measurements involve fractions, such as inches, centimeters, or liters.
- Finance: Calculating interest, discounts, or profits often involves working with fractions and percentages (which are essentially fractions expressed as parts of 100).
Beyond the Basics: Working with More Complex Fractions
While the problem "What is 1/7 of 28?" involves a relatively simple fraction, the principles extend to more complex scenarios. Let's consider some examples:
- Finding 3/7 of 28: Using the same methods as above, we can multiply (3/7) * 28. This simplifies to (3 * 28) / 7 = 84 / 7 = 12. Therefore, 3/7 of 28 is 12.
- Fractions with larger numbers: Imagine finding 5/12 of 72. This would involve multiplying (5/12) * 72 = (5 * 72) / 12 = 360 / 12 = 30.
- Improper Fractions: An improper fraction is where the numerator is greater than or equal to the denominator (e.g., 7/4). These fractions can be converted to mixed numbers (e.g., 1 3/4) or directly multiplied as shown in the examples above.
- Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 2 1/3). To perform calculations, it's often easier to convert the mixed number to an improper fraction first. For example, 2 1/3 is equivalent to (2*3 + 1)/3 = 7/3.
Developing Fractional Fluency: Tips and Tricks
Mastering fractions is a crucial building block for more advanced mathematical concepts. Here are some tips to enhance your understanding and skills:
- Practice Regularly: The more you practice working with fractions, the more confident and efficient you'll become.
- Visual Aids: Use diagrams, models, or real-world objects to visualize fractions and their relationships.
- Simplify Fractions: Always simplify fractions to their lowest terms. For example, 6/8 simplifies to 3/4.
- Understand Equivalent Fractions: Equivalent fractions represent the same value but have different numerators and denominators (e.g., 1/2 = 2/4 = 3/6).
- Use Online Resources: There are numerous websites and apps that offer interactive exercises and tutorials on fractions.
Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions is not just about solving mathematical problems; it's about developing a crucial life skill applicable across numerous domains. By understanding the methods for calculating fractions, visualizing their representations, and applying them to real-world situations, you equip yourself with a powerful tool for problem-solving and critical thinking. The simple question "What is 1/7 of 28?" serves as a gateway to a deeper understanding of this fundamental mathematical concept, opening doors to more complex calculations and a broader appreciation of the world around us. Keep practicing, and you'll soon find yourself effortlessly navigating the world of fractions.
Latest Posts
Latest Posts
-
Identify The Function That Best Models The Given Data
Jun 06, 2025
-
Use Number Line To Solve 235 123
Jun 06, 2025
-
A Food Handler Notices That A Cutting Surface Answer
Jun 06, 2025
-
A Silica Tetrahedron Molecule Contains Four
Jun 06, 2025
-
How Many Groups Of 3 4 Are In 11 4
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 7 Of 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.