What Is 12x3-9x2-4x+3 In Factored Form
Breaking News Today
Jun 02, 2025 · 5 min read
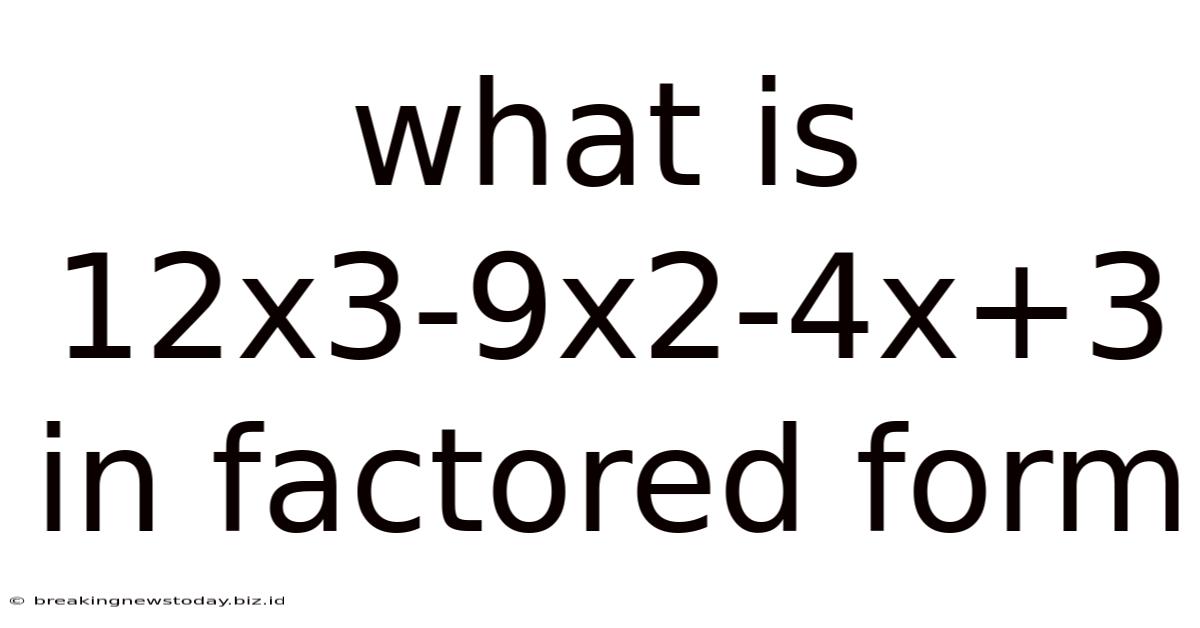
Table of Contents
What is 12x³ - 9x² - 4x + 3 in Factored Form? A Comprehensive Guide
Factoring polynomials is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding the behavior of functions. While some polynomials factor easily, others require more sophisticated techniques. This article delves into the process of factoring the cubic polynomial 12x³ - 9x² - 4x + 3, exploring multiple methods and providing a detailed explanation of each step. We'll also discuss the importance of factoring and its applications in various mathematical contexts.
Understanding Polynomial Factoring
Before tackling the specific problem, let's review the core concepts of polynomial factoring. Factoring a polynomial involves expressing it as a product of simpler polynomials. This process is the reverse of expanding polynomials using the distributive property (often referred to as FOIL for binomials). The goal is to find factors that, when multiplied together, yield the original polynomial.
Types of Factoring
Several techniques exist for factoring polynomials, including:
- Greatest Common Factor (GCF): This involves identifying the largest common factor among all terms and factoring it out.
- Difference of Squares: This applies to binomials of the form a² - b², which factors to (a + b)(a - b).
- Sum and Difference of Cubes: These are specialized formulas for factoring expressions like a³ + b³ and a³ - b³.
- Grouping: This method involves grouping terms with common factors to factor the expression.
- Rational Root Theorem: This theorem helps identify potential rational roots of a polynomial, which can then be used to find linear factors.
Factoring 12x³ - 9x² - 4x + 3: A Step-by-Step Approach
The polynomial 12x³ - 9x² - 4x + 3 doesn't readily factor using simple techniques like GCF or difference of squares. However, we can employ the grouping method and potentially the rational root theorem to find its factored form.
Method 1: Grouping
The grouping method involves strategically grouping terms to reveal common factors. Let's try this approach:
-
Group the terms: We can group the terms as follows: (12x³ - 9x²) + (-4x + 3)
-
Factor out the GCF from each group: In the first group, the GCF is 3x². In the second group, the GCF is -1. This gives us: 3x²(4x - 3) + (-1)(4x - 3)
-
Factor out the common binomial: Notice that both terms now share the common binomial (4x - 3). We can factor this out: (4x - 3)(3x² - 1)
Therefore, the factored form of 12x³ - 9x² - 4x + 3 using the grouping method is (4x - 3)(3x² - 1).
Method 2: Rational Root Theorem (Alternative Approach)
The Rational Root Theorem states that if a polynomial has a rational root p/q (where p and q are integers and q ≠ 0), then p must be a factor of the constant term, and q must be a factor of the leading coefficient.
-
Identify potential rational roots: For our polynomial, the constant term is 3, and the leading coefficient is 12. The factors of 3 are ±1 and ±3. The factors of 12 are ±1, ±2, ±3, ±4, ±6, and ±12. Therefore, the potential rational roots are ±1, ±3, ±1/2, ±3/2, ±1/3, ±1/4, ±1/6, ±1/12.
-
Test potential roots using synthetic division or direct substitution: We can test these potential roots by substituting them into the polynomial. If a root makes the polynomial equal to zero, then we've found a factor. Let's try x = 3/4:
12(3/4)³ - 9(3/4)² - 4(3/4) + 3 = 12(27/64) - 9(9/16) - 3 + 3 = 27/16 - 81/16 = 0
Since x = 3/4 is a root, (x - 3/4) is a factor. To eliminate the fraction, we can multiply by 4, giving us (4x - 3). Now we perform polynomial long division or synthetic division to find the other factor.
- Perform Polynomial Long Division or Synthetic Division: Dividing 12x³ - 9x² - 4x + 3 by (4x - 3) yields 3x² - 1.
Therefore, the factored form is again (4x - 3)(3x² - 1).
Verifying the Factored Form
To confirm our result, we can expand the factored form using the distributive property:
(4x - 3)(3x² - 1) = 4x(3x² - 1) - 3(3x² - 1) = 12x³ - 4x - 9x² + 3 = 12x³ - 9x² - 4x + 3
This matches the original polynomial, confirming the accuracy of our factoring.
Significance of Polynomial Factoring
Factoring polynomials is a vital tool in various mathematical applications, including:
- Solving Polynomial Equations: By factoring a polynomial equation, we can find its roots (or solutions) by setting each factor equal to zero. This is a powerful technique for solving many types of problems in mathematics and science.
- Simplifying Expressions: Factoring can simplify complex algebraic expressions, making them easier to manipulate and understand.
- Graphing Polynomials: The factored form of a polynomial reveals its x-intercepts (where the graph crosses the x-axis). This information is crucial for sketching the graph of the polynomial accurately.
- Calculus: Factoring is essential in calculus for finding derivatives, integrals, and limits.
- Real-World Applications: Polynomial functions are used to model various phenomena in physics, engineering, economics, and other fields. Factoring can help us understand and analyze these models more effectively.
Conclusion
Factoring the polynomial 12x³ - 9x² - 4x + 3, as demonstrated above, leads to the factored form (4x - 3)(3x² - 1). This process highlights the importance of understanding various factoring techniques, such as grouping and the rational root theorem. The ability to factor polynomials is a cornerstone of algebra, impacting many areas of mathematics and its applications to the real world. Remember to always verify your factored form by expanding it to ensure it matches the original polynomial. This detailed explanation should equip you with a strong understanding of the process and its significance within a broader mathematical context.
Latest Posts
Latest Posts
-
Round 1567 32007235 To The Nearest Thousand
Jun 04, 2025
-
What Conflict Is Indicated By The Underlined Sentences
Jun 04, 2025
-
The President Of A Company Is Starting An Annuity
Jun 04, 2025
-
Is 536 Cm Greater Than 53 6 Dm
Jun 04, 2025
-
The Following Are Important Aspects Of Great Customer Service Except
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 12x3-9x2-4x+3 In Factored Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.