What Is 3 8 Of 800
Breaking News Today
Jun 08, 2025 · 5 min read
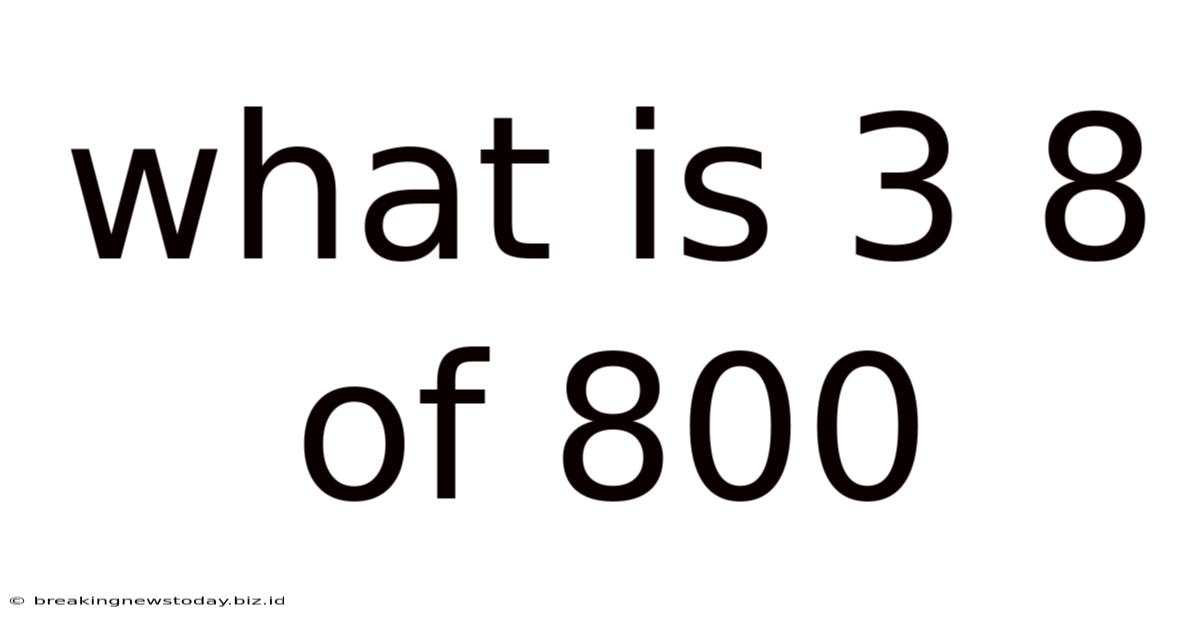
Table of Contents
What is 3/8 of 800? A Comprehensive Guide to Fractions and Percentages
Understanding fractions and percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in a shopping mall to determining the portion size of ingredients in a recipe. This article will delve into the solution of "What is 3/8 of 800?", providing a step-by-step explanation and exploring various approaches to solve similar problems. We'll also examine the broader context of fractions and their practical applications.
Understanding Fractions: A Quick Refresher
Before diving into the calculation, let's review the basics of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 3/8, 3 is the numerator and 8 is the denominator. This means we're dealing with 3 parts out of a total of 8 equal parts.
Calculating 3/8 of 800: The Step-by-Step Method
To find 3/8 of 800, we'll follow these steps:
Step 1: Convert the Fraction to a Decimal
The easiest way to calculate a fraction of a number is to convert the fraction into its decimal equivalent. We do this by dividing the numerator by the denominator:
3 ÷ 8 = 0.375
Step 2: Multiply the Decimal by the Whole Number
Now, multiply the decimal equivalent (0.375) by the whole number (800):
0.375 x 800 = 300
Therefore, 3/8 of 800 is 300.
Alternative Methods: Exploring Different Approaches
While the above method is straightforward, there are other ways to approach this problem:
Method 1: Working with Fractions Directly
Instead of converting to decimals, you can work directly with the fraction:
- Multiply the numerator by the whole number: 3 x 800 = 2400
- Divide the result by the denominator: 2400 ÷ 8 = 300
This method demonstrates the fundamental principle of fractions: multiplying the numerator by the whole number gives you the total number of parts, and then dividing by the denominator gives you the portion representing the fraction.
Method 2: Using Percentage Equivalents
Fractions and percentages are closely related. We can convert the fraction 3/8 into a percentage by dividing the numerator by the denominator and multiplying by 100:
(3 ÷ 8) x 100 = 37.5%
Then, calculate 37.5% of 800:
(37.5/100) x 800 = 300
This method highlights the interchangeability of fractions and percentages, showing that they represent the same proportional value.
Real-World Applications of Fraction Calculations
The ability to calculate fractions efficiently is crucial in numerous real-world scenarios:
- Cooking and Baking: Recipes often use fractions to specify ingredient amounts. Accurately calculating these fractions is essential for achieving the desired outcome.
- Shopping and Budgeting: Understanding discounts (often expressed as fractions or percentages) helps you determine the actual cost of an item.
- Construction and Engineering: Precise measurements and calculations involving fractions are fundamental in these fields.
- Data Analysis: Interpreting statistical data often requires working with fractions and percentages to represent proportions and trends.
- Finance: Calculating interest rates, loan repayments, and investment returns often involves intricate calculations with fractions and percentages.
Expanding on Fraction Concepts: Beyond the Basics
Understanding 3/8 of 800 is just one example of working with fractions. Let's explore some related concepts:
Equivalent Fractions: Different fractions can represent the same value. For instance, 3/8, 6/16, and 9/24 are all equivalent fractions. Understanding this concept helps simplify calculations and comparisons.
Simplifying Fractions: Reducing a fraction to its simplest form involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. For example, 6/16 simplifies to 3/8 by dividing both the numerator and denominator by 2 (the GCD).
Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than the denominator (e.g., 11/8). A mixed number combines a whole number and a fraction (e.g., 1 3/8). Converting between these forms is important for various calculations.
Adding, Subtracting, Multiplying, and Dividing Fractions: Mastering these operations is essential for more complex fraction-related problems. Remember, adding and subtracting fractions require a common denominator, while multiplying fractions involves multiplying numerators and denominators separately. Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction.
Solving Similar Problems: Practical Application and Tips
Once you understand the fundamental principles, you can easily apply them to other fraction problems. Here are some tips:
- Break it down: Complex problems can often be broken down into smaller, simpler steps.
- Visualize the problem: Using diagrams or drawings can help understand the concept more clearly, especially when dealing with visual learners.
- Practice regularly: The more you practice, the more comfortable and efficient you'll become in solving fraction problems.
- Use online resources: Numerous online calculators and tutorials are available to help with calculations and reinforce understanding.
- Understand the context: Pay close attention to the wording of the problem to ensure you're solving for the correct value.
Conclusion: Mastering Fractions for a Brighter Future
The ability to calculate fractions effectively is a valuable skill that extends far beyond the classroom. It’s a cornerstone of mathematical literacy, essential for navigating various aspects of daily life, professional pursuits, and problem-solving in general. By understanding the fundamental concepts, mastering different calculation methods, and practicing regularly, you can build confidence and proficiency in working with fractions, ensuring success in both academic and real-world applications. Remember that the solution to "What is 3/8 of 800?" – 300 – is a stepping stone to a broader understanding of fractions and their significant role in various fields.
Latest Posts
Latest Posts
-
Why Does The Author Include These Sentences
Jun 08, 2025
-
Which Statement Accurately Interprets The Information On The Chart
Jun 08, 2025
-
When Providing Hair Augmentation Services Cosmetologists Should
Jun 08, 2025
-
Classify Each Pair Of Angles As One Of The Following
Jun 08, 2025
-
Which Three Actions Demonstrate Jumping To Conclusions When Listening
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 8 Of 800 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.