What Is The Additive Inverse Of The Polynomial 9xy2+6x2y-5x3
Breaking News Today
Jun 04, 2025 · 4 min read
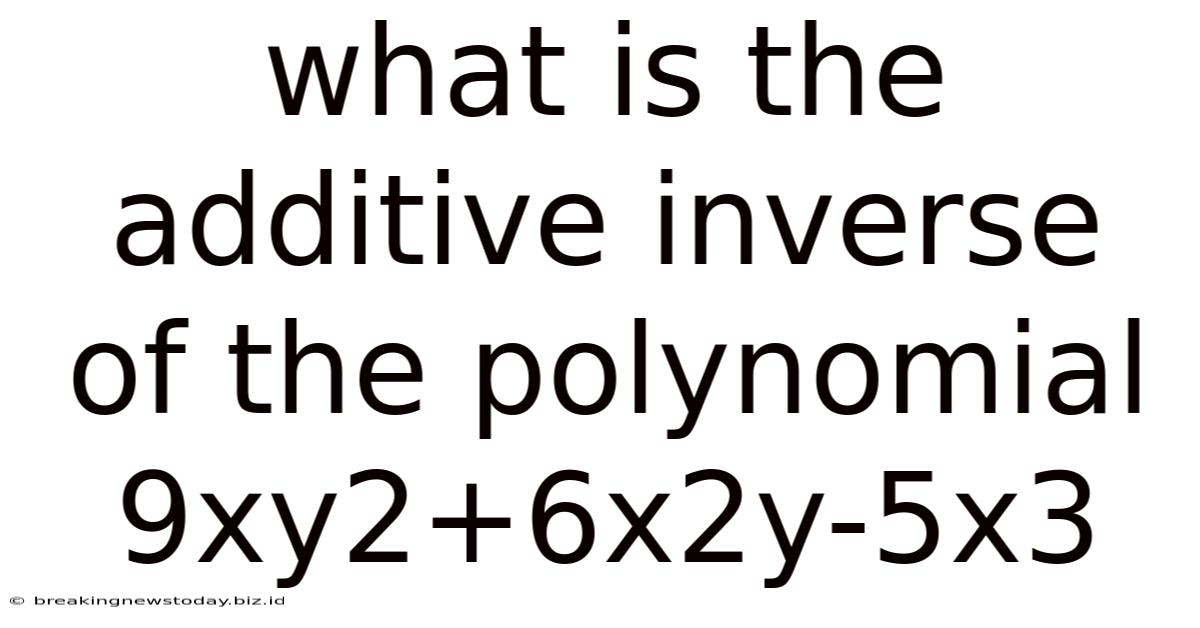
Table of Contents
What is the Additive Inverse of the Polynomial 9xy² + 6x²y - 5x³? A Deep Dive into Polynomial Arithmetic
Understanding additive inverses is fundamental in algebra, particularly when working with polynomials. This article will thoroughly explore the concept of additive inverses, specifically focusing on finding the additive inverse of the polynomial 9xy² + 6x²y - 5x³. We'll break down the process step-by-step, explaining the underlying principles and providing practical examples. Beyond just finding the answer, we'll delve into the broader implications of additive inverses in polynomial operations and their significance in various mathematical contexts.
Understanding Additive Inverses
Before we tackle the specific polynomial, let's establish a solid understanding of what an additive inverse is. In simple terms, the additive inverse of a number or expression is the value that, when added to the original number or expression, results in zero (the additive identity).
Example: The additive inverse of 5 is -5, because 5 + (-5) = 0. Similarly, the additive inverse of -7 is 7, because -7 + 7 = 0.
Extending the Concept to Polynomials
The concept of additive inverses extends seamlessly to polynomials. A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The additive inverse of a polynomial is the polynomial that, when added to the original polynomial, results in a zero polynomial (a polynomial where all coefficients are zero).
Finding the Additive Inverse: A Step-by-Step Guide
To find the additive inverse of the polynomial 9xy² + 6x²y - 5x³, we need to change the sign of each term in the polynomial. This is because adding a negative of a term effectively cancels it out.
1. Identify each term: Our polynomial has three terms:
- 9xy²
- 6x²y
- -5x³
2. Change the sign of each term: To find the additive inverse, we simply change the sign of each coefficient:
- The additive inverse of 9xy² is -9xy²
- The additive inverse of 6x²y is -6x²y
- The additive inverse of -5x³ is 5x³
3. Combine the terms: Now we combine these additive inverses to form the additive inverse polynomial:
-9xy² - 6x²y + 5x³
Therefore, the additive inverse of the polynomial 9xy² + 6x²y - 5x³ is -9xy² - 6x²y + 5x³.
Verification: Adding the Polynomial and its Additive Inverse
Let's verify our result by adding the original polynomial and its additive inverse:
(9xy² + 6x²y - 5x³) + (-9xy² - 6x²y + 5x³)
Combining like terms:
9xy² + (-9xy²) + 6x²y + (-6x²y) - 5x³ + 5x³ = 0
As you can see, the sum is zero, confirming that -9xy² - 6x²y + 5x³ is indeed the additive inverse of 9xy² + 6x²y - 5x³.
Additive Inverses and Polynomial Operations
Understanding additive inverses is crucial for several polynomial operations:
-
Subtraction: Subtracting a polynomial is equivalent to adding its additive inverse. For example, subtracting (9xy² + 6x²y - 5x³) from another polynomial is the same as adding (-9xy² - 6x²y + 5x³).
-
Solving Polynomial Equations: Additive inverses play a vital role in isolating variables and solving polynomial equations. For instance, consider the equation: P(x) + Q(x) = R(x). To find P(x), we would add the additive inverse of Q(x) to both sides of the equation.
-
Simplifying Expressions: Additive inverses can be used to simplify complex polynomial expressions by canceling out terms.
Beyond the Basics: Additive Inverses in Advanced Algebra
The concept of additive inverses extends far beyond basic polynomial arithmetic. It forms the foundation of more advanced algebraic structures:
-
Rings and Fields: In abstract algebra, rings and fields are algebraic structures with operations analogous to addition and multiplication. The concept of additive inverse is a defining property of these structures.
-
Vector Spaces: In linear algebra, vector spaces are sets of vectors equipped with vector addition and scalar multiplication. Each vector has an additive inverse, enabling the subtraction of vectors.
-
Group Theory: Additive inverses are integral to group theory, a branch of abstract algebra focusing on algebraic structures with a single binary operation satisfying specific axioms. The additive inverse is the inverse element under the group operation.
Practical Applications: Why are Additive Inverses Important?
While the concept might seem abstract, understanding additive inverses is crucial in many practical applications:
-
Computer Science: In computer programming, additive inverses are essential for performing arithmetic operations on integers and floating-point numbers, especially in situations involving negative numbers and representing numbers in binary or other numerical systems.
-
Engineering: Many engineering disciplines, such as electrical engineering and mechanical engineering, rely heavily on solving systems of equations, which often involve polynomial manipulations requiring the use of additive inverses.
-
Physics: In physics, particularly in areas like classical mechanics and electromagnetism, the mathematical modeling of various phenomena often involves the solution of polynomial equations that utilize the concept of additive inverses.
Conclusion: Mastering Additive Inverses
The seemingly simple concept of an additive inverse is, in reality, a cornerstone of algebra and many branches of mathematics. Understanding how to find the additive inverse of a polynomial, such as 9xy² + 6x²y - 5x³, is a fundamental skill that lays the groundwork for more advanced mathematical concepts and their applications in various fields. By grasping this fundamental principle, you enhance your problem-solving abilities and gain a deeper appreciation for the underlying structure of mathematics. Mastering additive inverses empowers you to tackle increasingly complex mathematical challenges with confidence and efficiency.
Latest Posts
Latest Posts
-
Name Two Ways Americans Used Steel
Jun 06, 2025
-
What Is The Unfinished Work Lincoln Mentions In Paragraph 3
Jun 06, 2025
-
Which Characteristic Best Identifies An Arrhenius Base
Jun 06, 2025
-
Which Triangle Is Similar To Triangle T
Jun 06, 2025
-
Which Generalization Is Supported By The Information In The Chart
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Additive Inverse Of The Polynomial 9xy2+6x2y-5x3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.