What Is The Gcf Of 96x5 And 64x2
Breaking News Today
Jun 06, 2025 · 5 min read
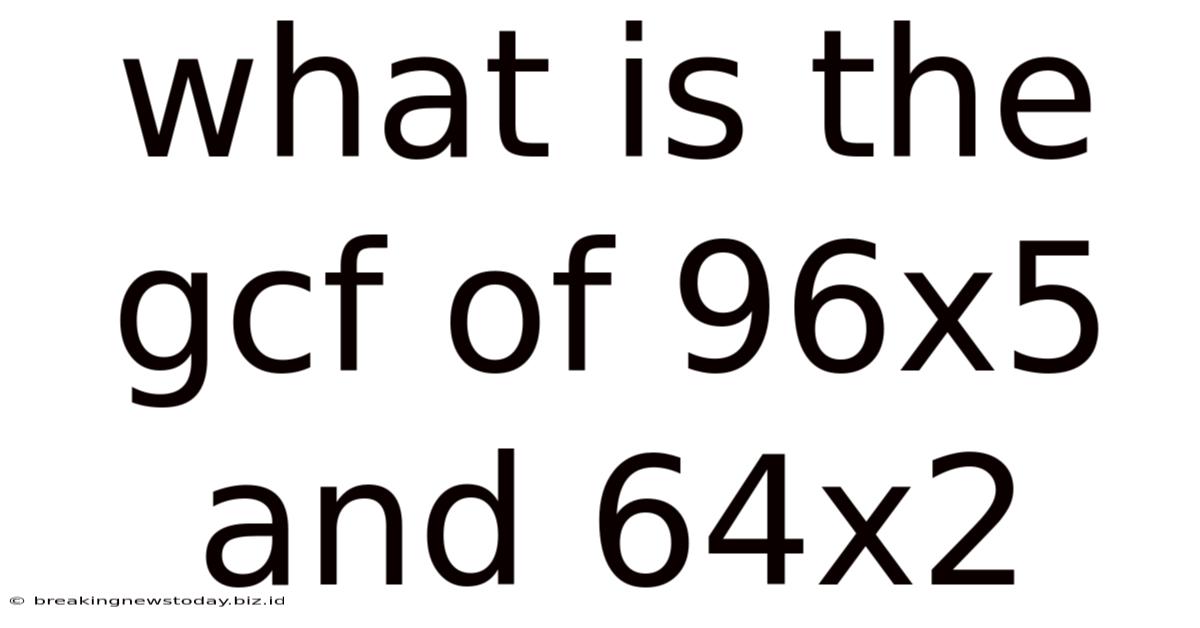
Table of Contents
What is the GCF of 96x⁵ and 64x²? A Comprehensive Guide
Finding the greatest common factor (GCF) of algebraic expressions involves a combination of number theory and algebraic manipulation. This guide will walk you through the process of determining the GCF of 96x⁵ and 64x², explaining the concepts involved in a clear and concise manner. We'll delve into the methods, providing examples and addressing potential points of confusion, ensuring you understand not just the answer, but the why behind it.
Understanding the Fundamentals: GCF and Prime Factorization
Before tackling the problem, let's refresh our understanding of key concepts:
What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. In the context of algebraic expressions, it's the largest expression that divides evenly into both expressions.
Prime Factorization: The Key to Finding the GCF
Prime factorization is the cornerstone of finding the GCF. It involves expressing a number as the product of its prime factors – numbers divisible only by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This method allows us to identify the common factors easily.
Finding the GCF of 96 and 64
Let's start by finding the GCF of the numerical coefficients 96 and 64. We'll use prime factorization:
- Prime factorization of 96: 2 x 2 x 2 x 2 x 2 x 3 = 2⁵ x 3
- Prime factorization of 64: 2 x 2 x 2 x 2 x 2 x 2 = 2⁶
Now, identify the common prime factors and their lowest powers:
Both numbers share five factors of 2. Therefore, the GCF of 96 and 64 is 2⁵ = 32.
Incorporating the Variables: x⁵ and x²
Now let's consider the variable part of the expressions: x⁵ and x².
The variable x is common to both terms. To find the GCF of the variable terms, we take the lowest power of the common variable. In this case, the lowest power is x².
Combining the Numerical and Variable GCFs
We've found the GCF of the numerical coefficients (32) and the variable part (x²). To get the GCF of the entire expressions 96x⁵ and 64x², we simply multiply these together:
GCF(96x⁵, 64x²) = 32x²
Therefore, the greatest common factor of 96x⁵ and 64x² is 32x².
Alternative Methods for Finding the GCF
While prime factorization is a reliable method, especially for larger numbers, alternative approaches exist:
The Listing Method (Suitable for Smaller Numbers)
This method involves listing all the factors of each number and identifying the largest common factor. Let's illustrate with smaller numbers for clarity:
Find the GCF of 12 and 18:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
The common factors are 1, 2, 3, and 6. The greatest common factor is 6.
While this method is simple for smaller numbers, it becomes less efficient as numbers grow larger.
The Euclidean Algorithm (For Larger Numbers)
The Euclidean algorithm is a more efficient method for finding the GCF of larger numbers. It's based on repeated division until the remainder is zero. The last non-zero remainder is the GCF.
Let's find the GCF of 96 and 64 using the Euclidean algorithm:
- Divide the larger number (96) by the smaller number (64): 96 ÷ 64 = 1 with a remainder of 32.
- Replace the larger number with the smaller number (64) and the smaller number with the remainder (32): 64 ÷ 32 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 32.
This method is particularly useful for very large numbers where prime factorization becomes cumbersome.
Applications of Finding the GCF
Understanding and applying the concept of the greatest common factor has numerous applications in various mathematical fields:
Simplifying Fractions
The GCF is crucial for simplifying fractions to their lowest terms. By dividing both the numerator and denominator by their GCF, we obtain an equivalent fraction in its simplest form. For example, simplifying 96/64:
96/64 = (96 ÷ 32) / (64 ÷ 32) = 3/2
Factoring Algebraic Expressions
Finding the GCF is the first step in factoring algebraic expressions. Factoring simplifies expressions, making them easier to manipulate and solve equations. For instance, factoring 96x⁵ - 64x²:
96x⁵ - 64x² = 32x²(3x³ - 2)
Solving Equations
The GCF plays a role in solving certain types of equations, particularly those involving factoring.
Advanced Concepts and Extensions
The principles of finding the GCF extend to more complex scenarios:
Polynomials with Multiple Variables
The same principles apply when finding the GCF of polynomials with multiple variables. For example, finding the GCF of 12x²y³ and 18x³y²:
- GCF of 12 and 18 is 6.
- GCF of x² and x³ is x².
- GCF of y³ and y² is y².
Therefore, the GCF of 12x²y³ and 18x³y² is 6x²y².
GCF of More Than Two Expressions
The process extends seamlessly to finding the GCF of more than two expressions. Find the prime factorization of each expression and identify the common prime factors with their lowest powers.
Conclusion: Mastering GCF for Mathematical Proficiency
Finding the greatest common factor is a fundamental skill in mathematics, applicable across various areas. Mastering this concept, through understanding prime factorization and employing efficient methods like the Euclidean algorithm, empowers you to simplify expressions, solve equations, and tackle more advanced mathematical problems with confidence. Remember, the key is to break down the problem into manageable parts—handling the numerical coefficients and variable parts separately before combining the results. This step-by-step approach ensures accuracy and a deeper understanding of the underlying mathematical principles.
Latest Posts
Latest Posts
-
Which Scenario Portrays A Round Character
Jun 07, 2025
-
Nutrients That Are Deemed To Be Essential Are Those Which
Jun 07, 2025
-
Which Of The Following Is A Fundamental Hairstyling Rule
Jun 07, 2025
-
Rainforests Are Principally Responsible For Global Oxygen Turnover
Jun 07, 2025
-
Plot All Ordered Pairs For The Values In The Domain
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 96x5 And 64x2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.