What Is The Greatest Common Factor Of 12a And 9a2
Breaking News Today
Jun 04, 2025 · 5 min read
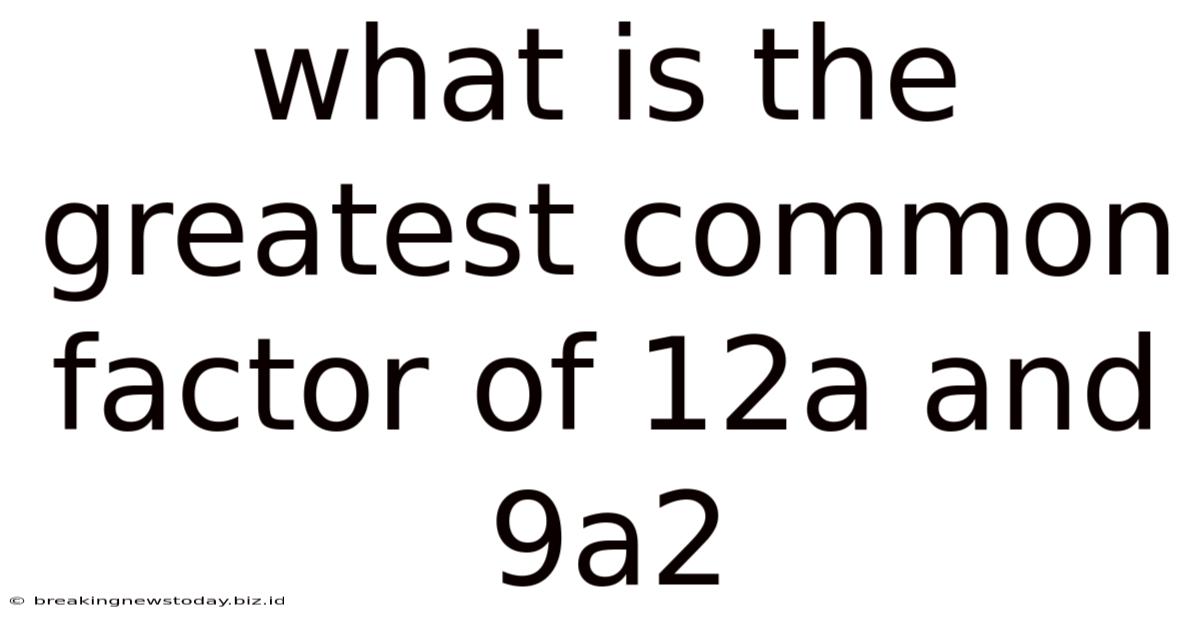
Table of Contents
What is the Greatest Common Factor of 12a and 9a²? A Deep Dive into GCF
Finding the greatest common factor (GCF) is a fundamental concept in mathematics, particularly crucial in algebra and number theory. This seemingly simple operation forms the bedrock of many advanced mathematical procedures. Understanding how to determine the GCF, especially when dealing with variables like in the expression 12a and 9a², is essential for simplifying expressions, solving equations, and generally mastering algebraic manipulation. This article will delve deep into finding the GCF of 12a and 9a², explaining the process step-by-step and exploring its broader implications.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific problem of finding the GCF of 12a and 9a², let's establish a solid understanding of the concept itself. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides evenly into two or more numbers without leaving a remainder. For instance, the GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 perfectly.
This concept extends beyond just numbers; it applies equally to algebraic expressions containing variables. In these cases, we need to consider both the numerical coefficients and the variables involved.
Finding the GCF of 12a and 9a²: A Step-by-Step Approach
Now, let's apply this knowledge to find the GCF of 12a and 9a². We'll break down the process into manageable steps:
Step 1: Find the GCF of the Coefficients
First, we consider the numerical coefficients: 12 and 9. We need to find the largest number that divides both 12 and 9 without leaving a remainder. This can be done using a few methods:
-
Listing Factors: List all the factors of 12 (1, 2, 3, 4, 6, 12) and all the factors of 9 (1, 3, 9). The largest factor they share is 3.
-
Prime Factorization: Break down each number into its prime factors. 12 = 2 x 2 x 3, and 9 = 3 x 3. The common prime factor is 3. Therefore, the GCF of 12 and 9 is 3.
Step 2: Find the GCF of the Variables
Next, we analyze the variables: 'a' and 'a²'. Remember that 'a²' means 'a x a'. The common variable is 'a', and the lowest power of 'a' present in both terms is 'a¹' or simply 'a'.
Step 3: Combine the Results
To find the GCF of 12a and 9a², we combine the GCF of the coefficients (3) and the GCF of the variables (a). Therefore, the greatest common factor of 12a and 9a² is 3a.
Verifying the GCF
To verify our result, let's see if 3a divides both 12a and 9a² evenly:
- 12a ÷ 3a = 4 (This division results in a whole number)
- 9a² ÷ 3a = 3a (This division also results in a whole number)
Since both divisions yield whole numbers, our GCF of 3a is correct.
Applications of Finding the GCF
Finding the greatest common factor is far more than a simple mathematical exercise. It's a crucial tool with diverse applications in various mathematical contexts:
1. Simplifying Algebraic Expressions
The GCF plays a significant role in simplifying algebraic expressions. By factoring out the GCF, we can reduce the complexity of an expression, making it easier to work with. For example, consider the expression 12a + 9a². We can factor out the GCF (3a) to obtain:
3a(4 + 3a)
This simplified form is much more concise and manageable than the original expression.
2. Solving Equations
GCF often comes into play when solving equations, particularly those involving factoring. Consider a quadratic equation like:
3x² + 6x = 0
Factoring out the GCF (3x) gives:
3x(x + 2) = 0
This allows us to find the solutions to the equation more easily (x = 0 or x = -2).
3. Fraction Simplification
The GCF is essential for simplifying fractions, both numerical and algebraic. By dividing both the numerator and denominator by their GCF, we can reduce the fraction to its simplest form. For instance, to simplify the fraction 12a/9a², we would divide both the numerator and denominator by the GCF (3a):
(12a ÷ 3a) / (9a² ÷ 3a) = 4/3a
This simplified fraction is easier to understand and work with.
4. Number Theory
In number theory, the GCF is fundamental to understanding concepts like relatively prime numbers (numbers whose GCF is 1), and the Euclidean algorithm, a method for computing the GCF of two integers. These concepts underpin many cryptographic systems and other advanced mathematical applications.
Beyond the Basics: Exploring More Complex Scenarios
While finding the GCF of 12a and 9a² is a relatively straightforward process, the concept extends to more complex scenarios involving:
-
Polynomials: Finding the GCF of polynomials involves identifying the common factors of both the coefficients and the variables within the terms. This often requires factoring the polynomial expressions before determining the GCF.
-
Multiple Terms: The GCF can be applied to more than two terms. Simply find the common factors among all the terms involved.
-
Negative Coefficients: When dealing with negative coefficients, consider the absolute value of the coefficients when finding the numerical GCF. The overall GCF might still include a negative sign if all terms have negative coefficients.
Conclusion: Mastering the GCF for Algebraic Success
The greatest common factor is a fundamental building block in algebra and beyond. Mastering its calculation, from simple cases like the GCF of 12a and 9a² to more intricate polynomial expressions, is critical for simplification, equation solving, and various other mathematical applications. This article has provided a comprehensive guide to understanding and utilizing the GCF, enhancing your skills in algebraic manipulation and preparing you for more complex mathematical challenges. By consistently applying these techniques, you’ll gain a deeper appreciation of this fundamental mathematical concept and its far-reaching impact across diverse areas of study. Remember to practice regularly, and you’ll find yourself effortlessly tackling GCF problems in the future.
Latest Posts
Latest Posts
-
Which Statement Best Describes Why Industry Uses Heterogeneous Catalysts
Jun 06, 2025
-
Two Rhombuses With The Same Side Lengths Are Always Congruent
Jun 06, 2025
-
Describe The Features Of The Volcanic Island After It Cools
Jun 06, 2025
-
A Typical Database Application Has How Many Layers
Jun 06, 2025
-
75 3 5 Y 4y 4y 6
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 12a And 9a2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.