What Is The Greatest Common Factor Of 4xy2 And 20x2y4
Breaking News Today
Jun 03, 2025 · 5 min read
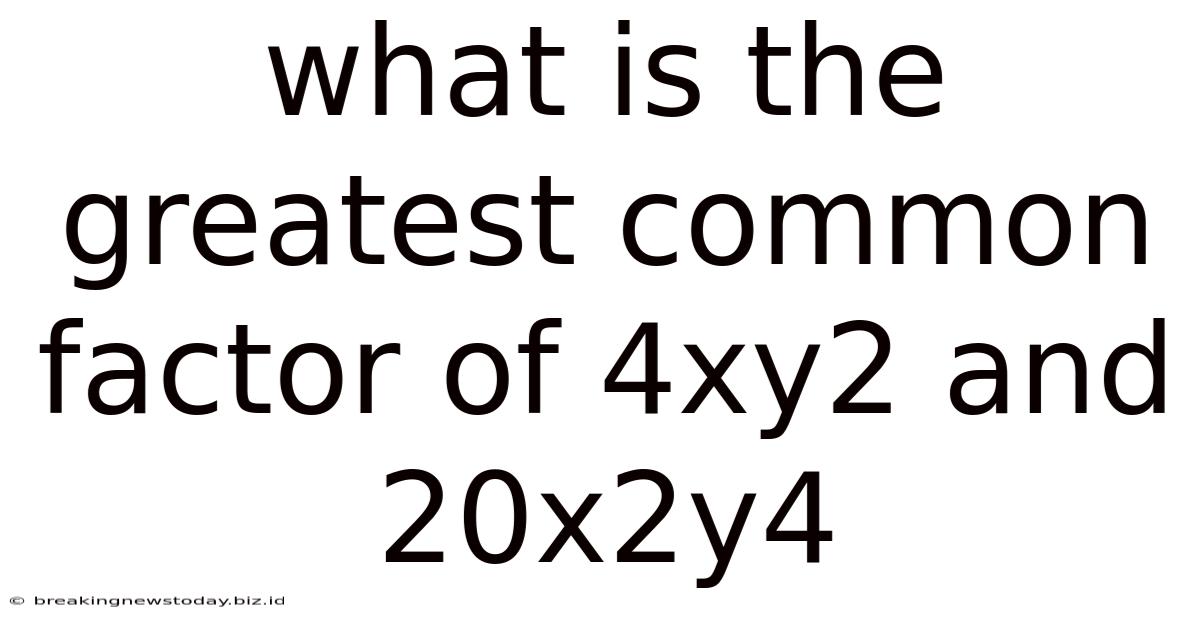
Table of Contents
What is the Greatest Common Factor of 4xy² and 20x²y⁴? A Deep Dive into Finding GCFs
Finding the greatest common factor (GCF) is a fundamental concept in mathematics, particularly crucial in simplifying algebraic expressions and solving equations. This article delves into the process of determining the GCF, specifically focusing on the example of 4xy² and 20x²y⁴. We'll explore the method step-by-step, providing a comprehensive understanding applicable to various similar problems. Furthermore, we'll discuss the broader implications of GCFs in algebra and beyond.
Understanding Greatest Common Factors (GCFs)
Before we tackle our specific problem, let's establish a solid understanding of what a greatest common factor represents. The GCF of two or more numbers or algebraic expressions is the largest number or expression that divides evenly into all of them without leaving a remainder. Think of it as the largest common "building block" shared by all the given terms.
For example, consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The greatest common factor is 6.
This concept extends seamlessly into algebra, where we deal with variables and exponents. The process remains the same: identify the common factors and select the largest one.
Finding the GCF of 4xy² and 20x²y⁴: A Step-by-Step Approach
Now, let's find the GCF of 4xy² and 20x²y⁴. We'll break down the process systematically:
1. Prime Factorization of Coefficients
First, we find the prime factorization of the numerical coefficients (the numbers in front of the variables).
- 4: 2 x 2 = 2²
- 20: 2 x 2 x 5 = 2² x 5
The common prime factor is 2², which is 4.
2. Identifying Common Variable Factors
Next, we examine the variable parts of the expressions:
- 4xy²: Contains one 'x' and two 'y's (x¹y²)
- 20x²y⁴: Contains two 'x's and four 'y's (x²y⁴)
To find the common variable factors, we select the lowest power of each variable present in both expressions.
- x: The lowest power is x¹ (or simply x).
- y: The lowest power is y².
3. Combining Common Factors to Find the GCF
Finally, we combine the common numerical and variable factors to determine the GCF:
GCF = 4xy²
Therefore, the greatest common factor of 4xy² and 20x²y⁴ is 4xy².
Practical Applications of GCFs
The ability to determine the greatest common factor is not just an abstract mathematical exercise; it has significant practical applications across various areas of mathematics and beyond:
1. Simplifying Algebraic Expressions
GCFs are essential for simplifying algebraic expressions. Consider the expression 4xy² + 20x²y⁴. By factoring out the GCF (4xy²), we can simplify the expression to:
4xy²(1 + 5xy²)
This simplified form is easier to work with in further calculations and analysis.
2. Solving Equations
GCFs play a vital role in solving certain types of equations. For instance, when solving quadratic equations by factoring, finding the GCF is often the first step in the process.
3. Fraction Reduction
In working with fractions, particularly algebraic fractions, finding the GCF of the numerator and denominator allows for simplification. This results in a more manageable and often more insightful representation of the fraction.
4. Geometry and Measurement
GCFs are used in geometry problems involving area and volume calculations, particularly when dealing with dimensions that share common factors. Finding the GCF can help simplify calculations and understand relationships between dimensions.
5. Real-World Applications
While less directly apparent, the underlying principles of finding common factors have applications in various real-world scenarios involving resource allocation, scheduling, and optimization problems. For instance, determining the most efficient way to package items of different sizes often involves finding common factors.
Expanding on the Concept: More Complex Examples
Let's extend our understanding by considering more complex scenarios involving GCFs.
Example 1: Three or More Expressions
Finding the GCF of three or more expressions involves the same process, but we need to consider all expressions simultaneously. Let's find the GCF of 6a²b³, 12a³b², and 18a⁴b.
- Coefficients: The GCF of 6, 12, and 18 is 6.
- Variables:
- 'a': The lowest power is a².
- 'b': The lowest power is b.
Therefore, the GCF of 6a²b³, 12a³b², and 18a⁴b is 6a²b.
Example 2: Expressions with Negative Coefficients
Negative coefficients don't change the core process, but we must consider the negative sign when identifying the GCF. Let's find the GCF of -8m³n² and 12m²n³.
- Coefficients: The GCF of 8 and 12 is 4. Since one coefficient is negative, we include the negative sign in the GCF.
- Variables:
- 'm': The lowest power is m².
- 'n': The lowest power is n².
Therefore, the GCF of -8m³n² and 12m²n³ is -4m²n².
Example 3: Expressions with Multiple Variables
Dealing with multiple variables simply requires us to apply the same procedure for each variable individually. Let's find the GCF of 15p²qr³ and 25pq²r.
- Coefficients: The GCF of 15 and 25 is 5.
- Variables:
- 'p': The lowest power is p.
- 'q': The lowest power is q.
- 'r': The lowest power is r.
Therefore, the GCF of 15p²qr³ and 25pq²r is 5pqr.
Conclusion: Mastering GCFs for Mathematical Success
Understanding and effectively calculating the greatest common factor is a cornerstone of algebraic manipulation and problem-solving. The techniques explored in this article—prime factorization, identification of common factors, and systematic combination—provide a robust framework for finding GCFs in various contexts, from simple numerical expressions to complex algebraic ones. Mastering this concept will undoubtedly improve your proficiency in algebra and related mathematical fields. Remember to practice with diverse examples to build confidence and fluency in applying these techniques. The more you practice, the more intuitive this essential mathematical skill will become.
Latest Posts
Latest Posts
-
The Revolving Component Of The Starter Is The
Jun 04, 2025
-
What Type Of Distribution Does This Giraffe Population Display
Jun 04, 2025
-
What Is One Advantage Of Using A Linear Plot Structure
Jun 04, 2025
-
A Food Handler Has Finished Grilling A Chicken
Jun 04, 2025
-
What Percent Of 250 Is 182
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 4xy2 And 20x2y4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.