What Is The Positive Solution Of X2 36 5x
Breaking News Today
May 10, 2025 · 4 min read
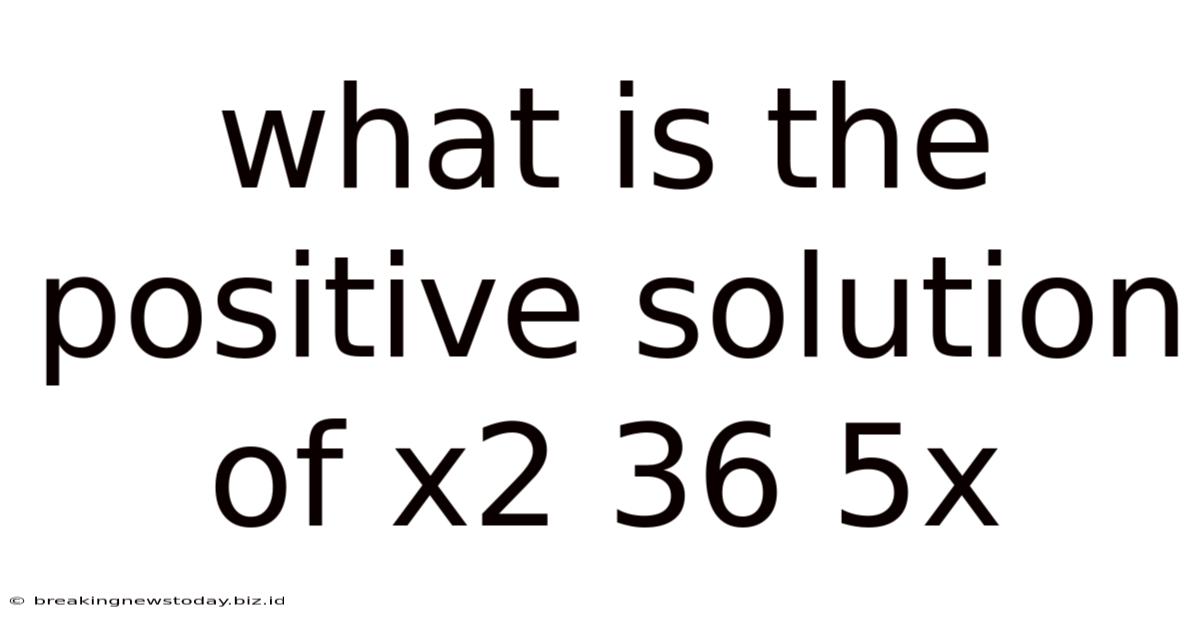
Table of Contents
Solving the Quadratic Equation: x² + 5x - 36 = 0
Finding the solutions to quadratic equations is a fundamental concept in algebra. This article delves into the process of solving the specific quadratic equation x² + 5x - 36 = 0, explaining multiple methods and focusing on identifying and interpreting the positive solution. We'll explore factorization, the quadratic formula, and completing the square, providing a comprehensive understanding of this common mathematical problem.
Understanding Quadratic Equations
A quadratic equation is an equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. The solutions to this equation, also known as roots or zeros, represent the x-values where the corresponding parabola intersects the x-axis. Our equation, x² + 5x - 36 = 0, fits this form with a = 1, b = 5, and c = -36.
Method 1: Factoring the Quadratic Equation
Factoring is a powerful method for solving quadratic equations, particularly when the factors are easily identifiable. The goal is to find two binomials whose product equals the original quadratic expression. In this case, we're looking for two numbers that add up to 5 (the coefficient of x) and multiply to -36 (the constant term).
These numbers are 9 and -4. Therefore, we can factor the equation as follows:
(x + 9)(x - 4) = 0
This equation is satisfied if either (x + 9) = 0 or (x - 4) = 0. Solving these gives us two solutions:
- x + 9 = 0 => x = -9
- x - 4 = 0 => x = 4
Therefore, the solutions to the quadratic equation x² + 5x - 36 = 0 are x = -9 and x = 4. The positive solution is x = 4.
Method 2: Using the Quadratic Formula
The quadratic formula provides a general solution for any quadratic equation. It's a reliable method, especially when factoring isn't straightforward. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 5, c = -36), we get:
x = [-5 ± √(5² - 4 * 1 * -36)] / (2 * 1) x = [-5 ± √(25 + 144)] / 2 x = [-5 ± √169] / 2 x = [-5 ± 13] / 2
This gives us two solutions:
- x = (-5 + 13) / 2 = 8 / 2 = 4
- x = (-5 - 13) / 2 = -18 / 2 = -9
Again, the solutions are x = 4 and x = -9. The positive solution remains x = 4.
Method 3: Completing the Square
Completing the square is another algebraic technique for solving quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
-
Move the constant term: Rewrite the equation as x² + 5x = 36
-
Complete the square: To complete the square, take half of the coefficient of x (which is 5/2), square it ((5/2)² = 25/4), and add it to both sides of the equation:
x² + 5x + 25/4 = 36 + 25/4
- Factor the perfect square trinomial: The left side is now a perfect square trinomial:
(x + 5/2)² = 169/4
- Solve for x: Take the square root of both sides:
x + 5/2 = ±√(169/4) = ±13/2
- Isolate x:
x = -5/2 ± 13/2
This leads to the same two solutions:
- x = (-5/2 + 13/2) = 8/2 = 4
- x = (-5/2 - 13/2) = -18/2 = -9
Once more, the positive solution is x = 4.
Understanding the Solutions in Context
The solutions x = 4 and x = -9 represent the points where the parabola represented by the equation y = x² + 5x - 36 intersects the x-axis. These are the x-intercepts of the parabola. The positive solution, x = 4, indicates a specific point on the positive x-axis where the parabola crosses.
Applications of Quadratic Equations
Quadratic equations appear frequently in various fields, including:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity.
- Engineering: Designing structures, analyzing stresses and strains in materials.
- Economics: Modeling supply and demand, optimizing profit functions.
- Computer Graphics: Creating curves and shapes.
Understanding how to solve quadratic equations is crucial for tackling problems in these and other disciplines.
Further Exploration: Discriminant and Nature of Roots
The expression b² - 4ac within the quadratic formula is called the discriminant. The discriminant helps determine the nature of the roots:
- b² - 4ac > 0: Two distinct real roots (as in our example).
- b² - 4ac = 0: One real root (a repeated root).
- b² - 4ac < 0: Two complex roots (involving imaginary numbers).
In our case, the discriminant is 169 (5² - 4 * 1 * -36 = 169), which is greater than 0, indicating two distinct real roots.
Conclusion
Solving the quadratic equation x² + 5x - 36 = 0, using factoring, the quadratic formula, or completing the square, consistently yields the solutions x = 4 and x = -9. The positive solution is unequivocally x = 4. This comprehensive analysis emphasizes the importance of understanding multiple solution methods and interpreting the results within the context of quadratic equations and their applications. Mastering these techniques is fundamental to success in algebra and related fields. Remember to always check your solutions by substituting them back into the original equation to verify their accuracy.
Latest Posts
Latest Posts
-
Job Site Fire Prevention Is The Principal Responsibility Of
May 10, 2025
-
Venn Diagram For Prokaryotic And Eukaryotic Cells
May 10, 2025
-
In 1979 Iranian Militant Groups Took Hostage In Tehran
May 10, 2025
-
Which Statement About Jupiters Moon Io Is True
May 10, 2025
-
Post Secondary Education And Training Is An Inexpensive And Minor Investment
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Positive Solution Of X2 36 5x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.