What Is The Range Of Y 3sin X 4
Breaking News Today
Jun 06, 2025 · 5 min read
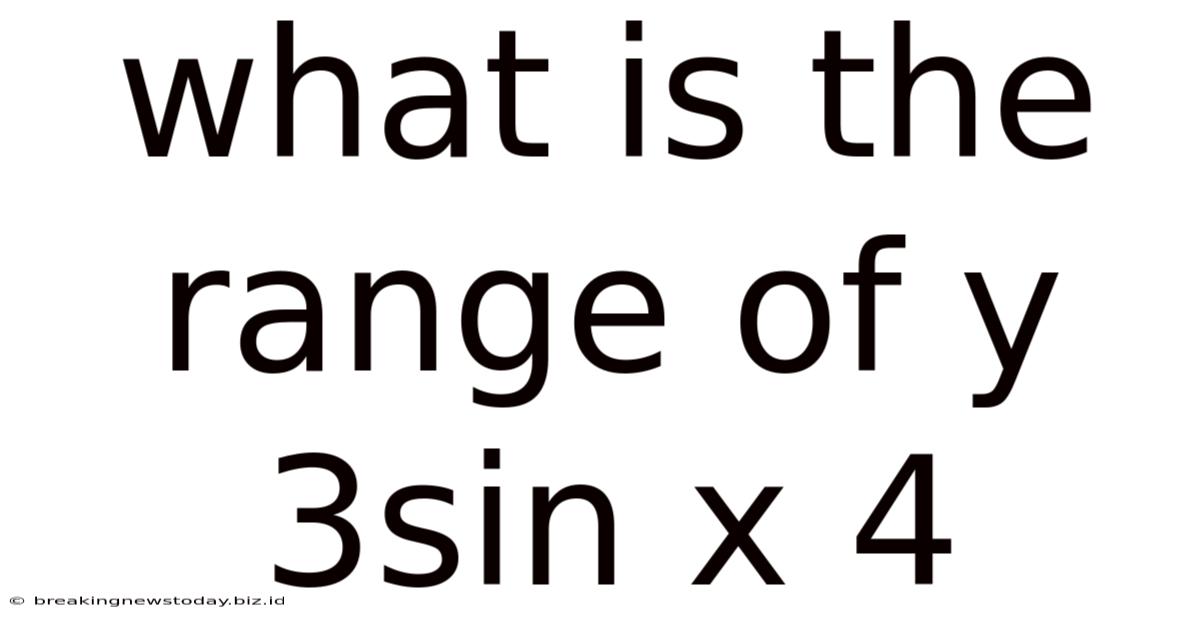
Table of Contents
Decoding the Range of y = 3sin x + 4: A Comprehensive Guide
Understanding the range of trigonometric functions is crucial for anyone working with graphs, equations, and their applications in various fields like physics, engineering, and computer graphics. This comprehensive guide will delve into the intricacies of determining the range of the function y = 3sin x + 4, providing a clear understanding of the process and the underlying mathematical principles. We'll explore the transformations involved, the impact of amplitude and vertical shift, and provide visual aids to solidify your understanding.
Understanding the Sine Function
Before tackling the given function, let's refresh our knowledge of the basic sine function, y = sin x. The sine function is a periodic function, meaning its values repeat over a regular interval. Its range is bounded between -1 and 1, inclusive. This means that the output of the sine function (the y-value) will always fall within this interval: -1 ≤ sin x ≤ 1.
Visualizing the Sine Wave
The graph of y = sin x is a wave that oscillates between -1 and 1 along the y-axis. This oscillation repeats every 2π units along the x-axis (its period). Understanding this wave is key to comprehending transformations and determining the range of more complex sine functions.
Transforming the Sine Function: y = 3sin x + 4
Our target function, y = 3sin x + 4, is a transformation of the basic sine function. It involves two key transformations:
-
Vertical Stretch (Amplitude): The coefficient 3 in front of the sin x stretches the graph vertically. The amplitude of the sine wave is now 3, meaning the maximum and minimum y-values will be three times farther from the midline than in the basic sine function.
-
Vertical Shift: The constant +4 shifts the entire graph upwards by 4 units. This affects the midline of the wave, which is the horizontal line around which the wave oscillates. The midline for y = sin x is y = 0; after a vertical shift of +4, the midline becomes y = 4.
Determining the Range
With these transformations in mind, we can determine the range of y = 3sin x + 4.
-
Effect of Amplitude: Since the amplitude is 3, the sine wave will now oscillate 3 units above and below its midline.
-
Effect of Vertical Shift: The midline is shifted upwards to y = 4.
-
Calculating the Maximum and Minimum Values: Combining the amplitude and vertical shift, the maximum value of y will be 4 + 3 = 7, and the minimum value will be 4 - 3 = 1.
Therefore, the range of y = 3sin x + 4 is 1 ≤ y ≤ 7.
Graphical Representation
Let's visualize this using a graph. Imagine the graph of y = sin x. First, stretch it vertically by a factor of 3, making the peaks reach 3 and the troughs reach -3. Then, shift the entire graph upwards by 4 units. The peaks will now reach 7 (3 + 4), and the troughs will reach 1 (-3 + 4). This clearly shows the range of the function is between 1 and 7, inclusive.
Comparing to the Basic Sine Function
To further solidify our understanding, let's contrast the range of y = 3sin x + 4 with the range of the basic sine function, y = sin x:
| Function | Range | Midline | Amplitude |
|---|---|---|---|
| y = sin x | -1 ≤ y ≤ 1 | y = 0 | 1 |
| y = 3sin x + 4 | 1 ≤ y ≤ 7 | y = 4 | 3 |
Notice how the amplitude and vertical shift directly impact the range. The amplitude determines the distance between the midline and the maximum/minimum values, while the vertical shift determines the position of the midline.
Generalizing the Approach
This approach can be generalized to any function of the form y = A sin(Bx + C) + D, where:
- A is the amplitude.
- B affects the period.
- C affects the horizontal shift (phase shift).
- D is the vertical shift.
The range of such a function will always be D - |A| ≤ y ≤ D + |A|. Remember that the absolute value of A is used because the amplitude represents the distance from the midline, regardless of whether the graph is flipped (inverted).
Applications and Real-World Examples
Understanding the range of trigonometric functions has numerous applications:
-
Modeling Oscillatory Phenomena: Sine waves are used extensively to model various oscillatory phenomena, such as sound waves, light waves, and the motion of pendulums. Knowing the range helps predict the maximum and minimum values of these oscillations.
-
Signal Processing: In signal processing, understanding the range of signals is vital for designing appropriate filters and processing techniques.
-
Computer Graphics: Trigonometric functions are fundamental in computer graphics for creating animations, transformations, and rendering realistic scenes. The range determines the bounds of the visual output.
-
Physics: Many physical phenomena are described using sinusoidal functions. For example, the range of a simple harmonic oscillator can be determined using the principles we've explored.
Advanced Considerations
For more advanced analysis, one might consider:
-
Domain: While the range focuses on the output values, the domain considers the input values (x-values). The sine function has an unbounded domain, meaning x can take any real number value.
-
Periodicity: The period of y = 3sin x + 4 is still 2π, the same as the basic sine function, because the transformations don't affect the period.
-
Inverse Functions: Understanding the range is crucial when considering the inverse function. A function must be one-to-one (have a unique output for each input) to have an inverse. Restricting the domain of a trigonometric function often becomes necessary to ensure the existence of its inverse.
Conclusion
Determining the range of y = 3sin x + 4 involves understanding the fundamental properties of the sine function and the effects of transformations like amplitude and vertical shift. Through a combination of mathematical analysis and visualization, we've demonstrated that the range is 1 ≤ y ≤ 7. This understanding is not just a theoretical exercise; it's essential for applying trigonometric functions to solve real-world problems across diverse fields. Remember the key principles of amplitude, vertical shift, and their impact on the range to confidently analyze and manipulate trigonometric functions in your future work.
Latest Posts
Latest Posts
-
An Example Of A Biological Pulpal Stimulus Is
Jun 06, 2025
-
The Quotient Of 2 And A Number X Times 3
Jun 06, 2025
-
The Gazebo In The Park Is An Octagon
Jun 06, 2025
-
A Pen And A Pencil Cost 55 Cents Together
Jun 06, 2025
-
Make The Following Word Plural El Papel
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Range Of Y 3sin X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.