What Is The Value Of 15i/2+i
Breaking News Today
Jun 08, 2025 · 4 min read
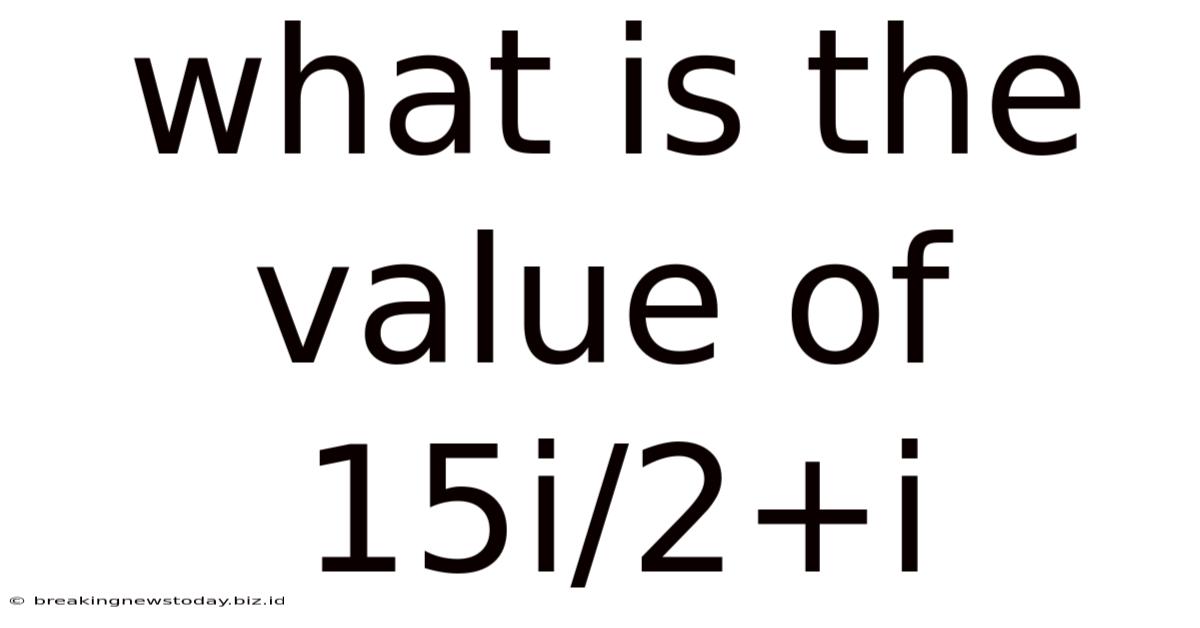
Table of Contents
Decoding Complex Numbers: Unveiling the Value of 15i/(2+i)
The realm of mathematics extends beyond the familiar world of real numbers. Dive into the fascinating world of complex numbers, where imaginary units dance alongside real numbers, unlocking solutions to equations previously unsolvable. This article delves into the process of evaluating the expression 15i/(2+i), a seemingly simple expression that reveals the elegant power and methodology of complex number arithmetic. We'll explore the concept of complex numbers, the significance of the imaginary unit 'i', and finally, calculate the value of our expression step-by-step. Prepare to unravel the intricacies of this mathematical puzzle!
Understanding Complex Numbers: Beyond the Real
Before tackling our expression, let's establish a solid foundation in complex numbers. A complex number is a number that can be expressed in the form a + bi, where:
- a is the real part of the complex number.
- b is the imaginary part of the complex number.
- i is the imaginary unit, defined as the square root of -1 (√-1).
The imaginary unit, 'i', is the cornerstone of complex numbers. It allows us to solve equations that have no solutions within the realm of real numbers, such as x² = -1. Without 'i', this equation would be deemed unsolvable. The introduction of complex numbers significantly expands the scope of mathematical possibilities.
The Conjugate: A Key to Simplification
To simplify expressions involving complex numbers, especially those with complex numbers in the denominator, we employ a powerful tool: the complex conjugate. The conjugate of a complex number a + bi is simply a - bi. Multiplying a complex number by its conjugate yields a real number, a crucial step in our calculation.
Solving 15i/(2+i): A Step-by-Step Guide
Now, let's tackle the expression 15i/(2+i). Our primary goal is to eliminate the complex number from the denominator. This is achieved by multiplying both the numerator and the denominator by the conjugate of the denominator.
Step 1: Identify the Conjugate
The denominator is (2+i). Its conjugate is (2-i).
Step 2: Multiply the Numerator and Denominator by the Conjugate
We multiply both the numerator and the denominator by (2-i):
[15i/(2+i)] * [(2-i)/(2-i)]
Step 3: Expand the Numerator
Expanding the numerator:
15i * (2 - i) = 30i - 15i²
Remember that i² = -1. Therefore, -15i² = -15(-1) = 15.
So, the expanded numerator becomes 15 + 30i.
Step 4: Expand the Denominator
Expanding the denominator using the difference of squares formula ((a+b)(a-b) = a² - b²):
(2+i)(2-i) = 2² - i² = 4 - (-1) = 5
Step 5: Simplify the Expression
Now, we have:
(15 + 30i) / 5
Step 6: Final Simplification
Dividing both the real and imaginary parts by 5:
15/5 + 30i/5 = 3 + 6i
Therefore, the value of 15i/(2+i) is 3 + 6i.
Visualizing Complex Numbers: The Complex Plane
Complex numbers can be represented graphically on the complex plane. The horizontal axis represents the real part (a), and the vertical axis represents the imaginary part (b). Our solution, 3 + 6i, can be plotted as a point with coordinates (3, 6) on the complex plane. This visual representation adds another layer of understanding to complex numbers.
Applications of Complex Numbers: A Wider Perspective
The seemingly abstract world of complex numbers finds surprisingly practical applications in diverse fields:
-
Electrical Engineering: Complex numbers are fundamental in analyzing alternating current (AC) circuits. They simplify calculations involving impedance, phase shifts, and resonance.
-
Signal Processing: Complex numbers are used extensively in Fourier analysis, a powerful tool for analyzing signals and extracting meaningful information.
-
Quantum Mechanics: Complex numbers are integral to the mathematical framework of quantum mechanics, describing the behavior of subatomic particles and quantum systems.
-
Fluid Dynamics: Complex analysis is employed in solving fluid flow problems, particularly those involving potential flow and conformal mapping.
Further Exploration: Beyond the Basics
This article provides a foundational understanding of complex numbers and demonstrates the calculation of 15i/(2+i). However, the world of complex numbers extends far beyond this basic operation. Further exploration might include:
-
Polar Form of Complex Numbers: Representing complex numbers in polar coordinates (magnitude and angle) offers advantages in certain calculations and visual representations.
-
Euler's Formula: This remarkable formula connects complex exponentials to trigonometric functions, revealing a deep connection between seemingly disparate mathematical concepts.
-
Complex Functions and Calculus: The extension of calculus to complex functions opens up a whole new realm of mathematical analysis, with applications in various scientific and engineering fields.
Conclusion: Embracing the Complexity
The expression 15i/(2+i) serves as a gateway to the fascinating and powerful world of complex numbers. Understanding complex number arithmetic is essential for anyone venturing into fields that utilize advanced mathematical tools. This article provides a solid foundation, encouraging further exploration and a deeper appreciation for the elegance and utility of complex numbers. The seemingly simple problem of evaluating this expression reveals the beauty and practical significance of complex number operations within a broader mathematical context. The journey into complex numbers is a journey of discovery, unveiling a world of solutions that lie beyond the limitations of real numbers alone.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Value Of 15i/2+i . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.