What Is The Value Of The 0 In 302
Breaking News Today
Jun 06, 2025 · 5 min read
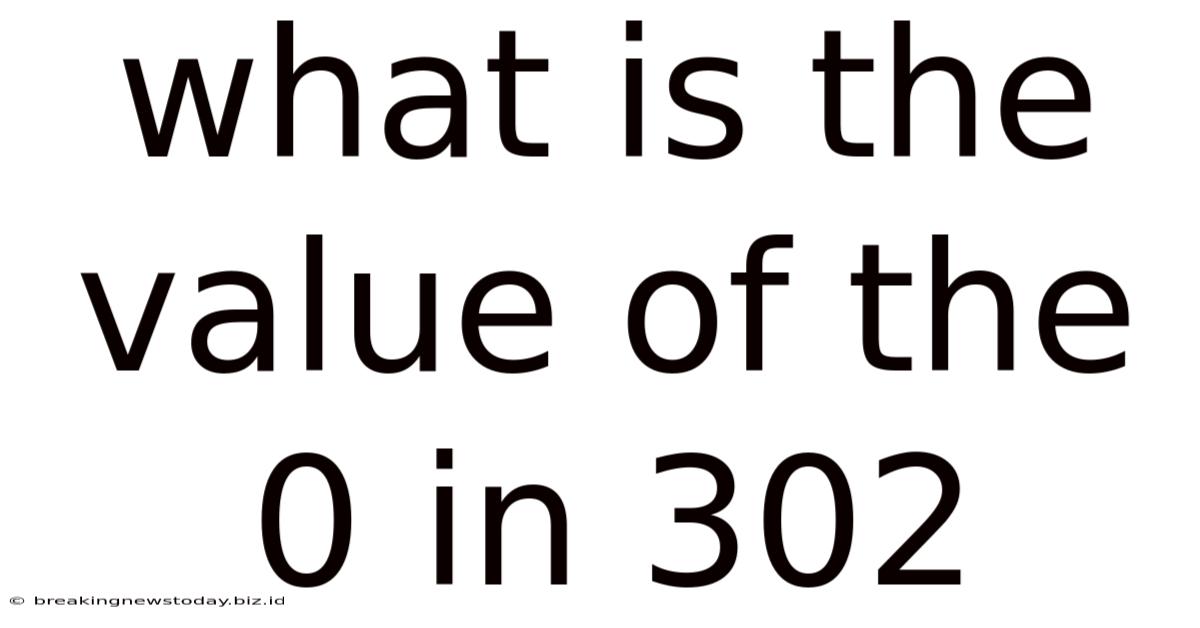
Table of Contents
Decoding the Value of Zero in 302: More Than Just a Placeholder
The number 302 might seem unremarkable at first glance. But a closer look reveals a fascinating interplay between place value and the subtle yet significant role of zero. Understanding the true value of the zero in 302 goes beyond simple arithmetic; it unlocks a deeper appreciation of our number system and its foundational principles. This article will delve into this seemingly simple concept, exploring its implications in mathematics, computer science, and even beyond.
The Power of Position: Understanding Place Value
Our number system is a positional system, meaning the value of a digit depends entirely on its position within the number. This is in stark contrast to older systems, like Roman numerals, where the value of a symbol remains constant regardless of its placement. Consider the number 302:
- 3 (Hundreds Place): This digit represents 3 x 100 = 300.
- 0 (Tens Place): This digit represents 0 x 10 = 0.
- 2 (Units/Ones Place): This digit represents 2 x 1 = 2.
The zero in 302, therefore, doesn't represent "nothingness" in the absolute sense. Instead, it acts as a placeholder, signifying the absence of tens. Without it, the number would be written as 32, a completely different value. This subtle distinction highlights the pivotal role zero plays in our positional number system. It's not just a lack of quantity; it's a crucial component of the structure itself.
The Zero's Contribution to Magnitude
The value of the zero in 302 directly influences the magnitude of the entire number. The zero pushes the digit 3 into the hundreds place, increasing the number's value significantly. Without the zero, we would have 32, a number one order of magnitude smaller than 302. This demonstrates the zero's critical function in representing larger quantities and distinguishing between numbers with differing scales.
Zero's Influence Beyond Basic Arithmetic
The significance of zero extends far beyond simple place value. Its impact is felt across various fields, showcasing its fundamental importance in mathematical operations and computational processes.
Zero in Arithmetic Operations:
- Addition: Zero is the additive identity; adding zero to any number leaves that number unchanged (e.g., 302 + 0 = 302).
- Subtraction: Subtracting zero from any number leaves that number unchanged (e.g., 302 - 0 = 302).
- Multiplication: Multiplying any number by zero results in zero (e.g., 302 x 0 = 0).
- Division: Dividing any number by zero is undefined, highlighting zero's unique properties and the inherent limitations of division.
These properties are crucial in algebra, calculus, and virtually all branches of mathematics. They provide a foundational structure for solving equations and understanding mathematical relationships.
Zero's Role in Computer Science
In computer science, zero holds even more significance. It forms the basis of binary code, the language of computers. Binary uses only two digits, 0 and 1, to represent all data. The zero and one represent the absence or presence of an electrical signal, respectively, forming the foundation for all digital computations. Without zero, binary code would be impossible, halting the advancement of modern computing.
Furthermore, zero is essential in several computer science concepts:
- Null values: In programming, zero often represents a null or empty value, indicating the absence of data. This is crucial for error handling and data management.
- Boolean logic: Zero frequently represents "false" in Boolean logic, the foundation of decision-making in computer programs.
- Addressing: Memory addresses often start at zero, enabling efficient memory management and data retrieval.
Zero and the Concept of Nothingness
While zero functions as a placeholder in our number system, its relationship to the philosophical concept of "nothingness" is complex and debated. Mathematically, zero is a number with specific properties and functions. Philosophically, nothingness represents the absence of existence. While they seem connected, they are distinct concepts.
The fact that we can represent "nothingness" with a symbol highlights the remarkable ingenuity of our number system. It allows us to express the absence of something within a numerical framework, enabling us to perform calculations and express relationships involving the absence of quantity.
Practical Applications of Understanding Zero's Value
Understanding the value of zero in numbers like 302 isn't just an academic exercise. It has real-world implications in various fields:
- Accounting and Finance: Accurate accounting requires a precise understanding of place value to avoid errors in recording and calculating financial transactions. A misplaced zero can lead to significant discrepancies.
- Engineering and Measurement: Engineers rely on precise measurements, and the proper use of zero is essential to ensure accuracy in blueprints, calculations, and construction.
- Data Science and Statistics: Data analysis requires a thorough understanding of numerical values, including the correct interpretation of zero in datasets and statistical calculations.
Beyond the Number 302: Extending the Concept
The principles discussed concerning the zero in 302 are applicable to any number where zero acts as a placeholder. Consider the number 10,000. The zeros here are crucial; they increase the magnitude by orders of magnitude. Without those zeros, the number would be drastically reduced in value. Similarly, consider numbers like 205 or 1024. Each zero holds a specific position and contributes to the overall value of the number.
Conclusion: The Unsung Hero of Our Number System
The zero in 302, while seemingly insignificant, is a crucial element that shapes the value and meaning of the entire number. Its role as a placeholder highlights the power of our positional number system. Beyond basic arithmetic, zero’s significance extends to computer science, philosophy, and numerous real-world applications. Therefore, understanding the value of zero isn't merely about arithmetic; it’s about appreciating the foundational principles that underpin our quantitative understanding of the world. The seemingly simple digit zero is, in reality, a powerful and essential component of our numerical language. It's the unsung hero that silently supports the intricate calculations and complex systems that shape our world.
Latest Posts
Latest Posts
-
Which Characteristic Guarantees That A Parallelogram Is A Rectangle
Jun 06, 2025
-
This Motivation Moves The Rising Action Toward What Event
Jun 06, 2025
-
Which Of The Following Definitions Best Describes The Term Devolution
Jun 06, 2025
-
Express 7 13 As A Repeating Decimal
Jun 06, 2025
-
A Manufacturer Of Cell Phone Screens
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of The 0 In 302 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.