What Is The Value Of X 105o 115o 125o 135o
Breaking News Today
Jun 02, 2025 · 5 min read
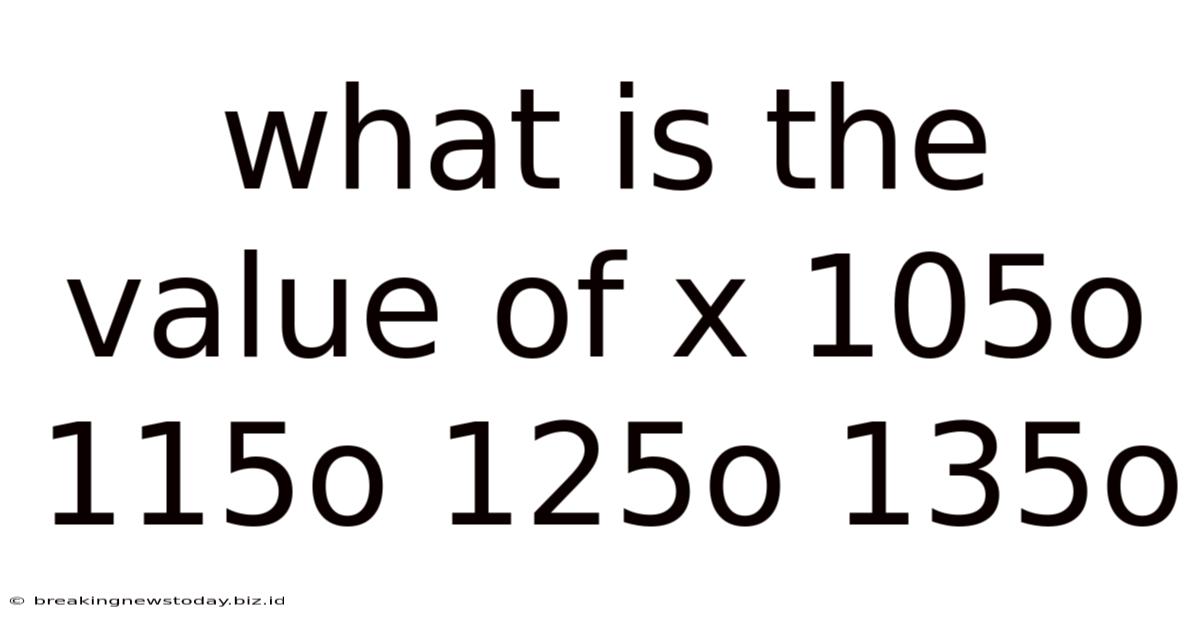
Table of Contents
What is the Value of x: Exploring Angles and Geometry
This article delves into the fascinating world of geometry, specifically focusing on solving for the unknown variable 'x' within a set of angles: 105°, 115°, 125°, and 135°. We'll explore various approaches to determine the value of x, depending on the context and the relationships between these angles. Understanding the underlying principles of angles, their classifications, and their relationships within geometric shapes is crucial for solving this type of problem.
Understanding Angles: A Quick Refresher
Before we jump into solving for x, let's refresh our understanding of angles. An angle is formed by two rays or line segments that share a common endpoint, called the vertex. Angles are measured in degrees (°), with a full circle encompassing 360°. We classify angles based on their measure:
- Acute Angle: An angle measuring less than 90°.
- Right Angle: An angle measuring exactly 90°.
- Obtuse Angle: An angle measuring greater than 90° but less than 180°.
- Straight Angle: An angle measuring exactly 180°.
- Reflex Angle: An angle measuring greater than 180° but less than 360°.
Scenario 1: Angles on a Straight Line
Let's consider a scenario where the angles 105°, 115°, 125°, and 135° are adjacent angles on a straight line. Angles on a straight line always add up to 180°. Therefore, if these angles are consecutive and form a straight line, the equation would be:
105° + 115° + 125° + 135° + x = 180°
This equation, however, doesn't make logical sense. The sum of the given angles alone exceeds 180°. Therefore, these angles cannot be adjacent angles on a straight line.
Scenario 2: Angles Around a Point
Another possibility is that the angles are located around a single point. The sum of angles around a point always equals 360°. If this is the case, our equation would be:
105° + 115° + 125° + 135° + x = 360°
Let's solve for x:
480° + x = 360°
x = 360° - 480°
x = -120°
A negative angle is possible, representing a clockwise rotation. Therefore, in this context, x = -120°. This solution indicates that an additional angle of -120° is needed to complete the 360° rotation around the point.
Scenario 3: Interior Angles of a Polygon
The angles could represent the interior angles of a polygon. However, we need to know the number of sides of the polygon to determine the sum of its interior angles. The formula for the sum of interior angles of an n-sided polygon is:
Sum of Interior Angles = (n - 2) * 180°
Let's explore some possibilities:
- If the polygon has 4 sides (quadrilateral): The sum of interior angles is (4-2) * 180° = 360°. In this case, the sum of given angles (480°) already exceeds 360°, making this scenario invalid.
- If the polygon has 5 sides (pentagon): The sum of interior angles is (5-2) * 180° = 540°. This would yield the equation: 480° + x = 540°, and solving for x gives x = 60°. This is a valid solution, suggesting that these angles could be interior angles of a pentagon.
- For polygons with more sides: As the number of sides increases, the sum of the interior angles increases, and a corresponding positive value of x can be found.
Therefore, depending on the shape and its number of sides, x can have a variety of values. It's crucial to know the geometrical context to definitively determine the value of x.
Scenario 4: Exterior Angles of a Polygon
Exterior angles, formed by extending one side of a polygon, also provide another perspective. The sum of exterior angles of any polygon always equals 360°. However, to use this, we'd need the exterior angles themselves, not the interior angles provided.
The Importance of Context in Geometry Problems
The examples above highlight the crucial role of context in solving geometric problems. Simply presenting a set of angles without specifying their relationship or the geometric figure they belong to is insufficient to determine the value of x definitively. To solve for x accurately, you must understand the specific geometric relationship between the angles involved.
Strategies for Solving Similar Problems
When encountering problems involving angles and unknown variables, follow these strategies:
-
Identify the Geometric Figure: Determine the type of geometric figure involved (triangle, quadrilateral, polygon, etc.).
-
Recall Relevant Angle Properties: Remember the properties of angles relevant to the figure (angles on a straight line, angles around a point, interior/exterior angles of polygons, etc.).
-
Formulate an Equation: Create an equation based on the properties identified, incorporating the given angles and the unknown variable 'x'.
-
Solve the Equation: Use algebraic techniques to solve for the value of 'x'.
-
Verify your Solution: Check your solution by plugging the value of x back into the equation and ensuring it satisfies the given conditions.
Conclusion: Beyond the Numbers
This exploration goes beyond simply finding the numerical value of x. It underscores the critical thinking required in geometry and problem-solving. The ambiguity inherent in the initial problem highlights the importance of clear context and complete information when dealing with geometric relationships. Remember, understanding the principles behind the numbers is just as important as finding the answer itself. By understanding angles, their classifications, and their properties within different geometric figures, you can confidently tackle similar problems and develop a deeper appreciation for the beauty and logic of geometry.
Latest Posts
Latest Posts
-
How Many Trapezoids Would Create 5 Hexagons
Jun 04, 2025
-
Which Geometric Figures Have A Measurable Quantity
Jun 04, 2025
-
How Effective Is It To Complete All Additional Requests
Jun 04, 2025
-
What Motif Appears In Both Haiku Night Flowers Water
Jun 04, 2025
-
247 Heart Beats In 6 1 2 Minutes
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of X 105o 115o 125o 135o . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.