What Percent Of 21.5 Is 55.04
Breaking News Today
Jun 06, 2025 · 5 min read
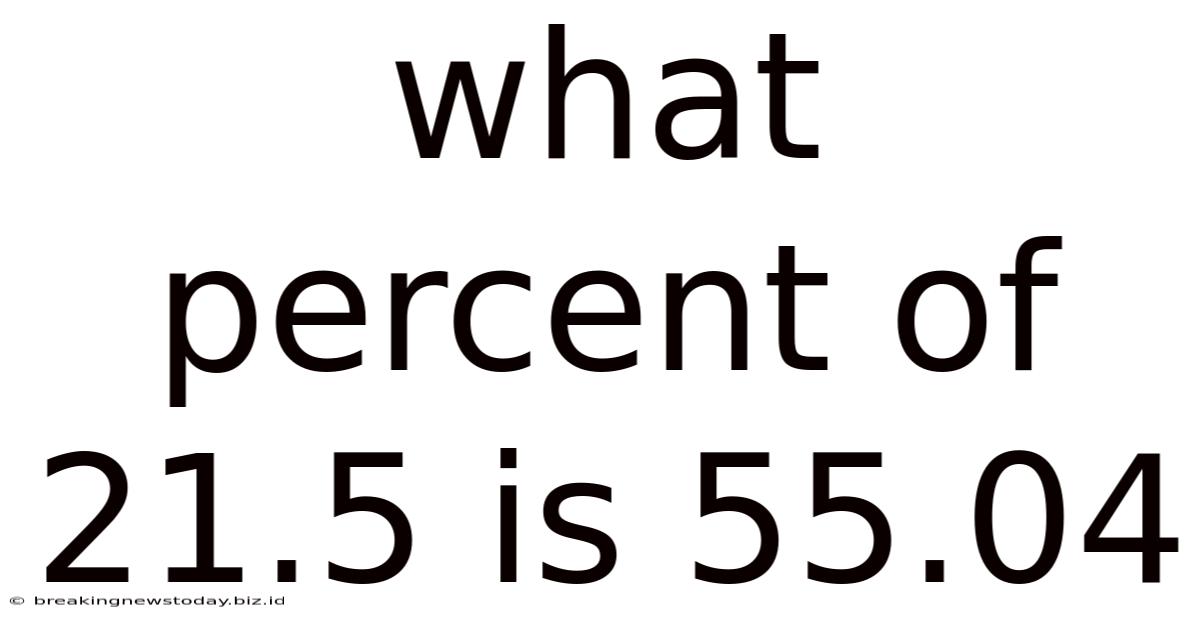
Table of Contents
What Percent of 21.5 is 55.04? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various fields, from finance and business to science and everyday life. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data accurately. This comprehensive guide will delve into the calculation of "What percent of 21.5 is 55.04?", exploring different methods, providing step-by-step instructions, and offering valuable insights into percentage calculations in general.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. It represents a proportion of a whole. The symbol "%" is used to denote percentages. For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
Method 1: Using the Formula
The most straightforward method to determine what percent of 21.5 is 55.04 involves using a basic percentage formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 55.04 (the number we want to express as a percentage of 21.5)
- Whole: 21.5 (the total or base number)
Let's plug the values into the formula:
(55.04 / 21.5) * 100 = Percentage
Calculating this gives us:
2.56 * 100 = 256%
Therefore, 55.04 is 256% of 21.5.
Method 2: Proportion Method
The proportion method offers an alternative approach to solving this percentage problem. This method sets up a proportion, equating two ratios:
(Part / Whole) = (Percentage / 100)
Substituting our values:
(55.04 / 21.5) = (x / 100)
To solve for 'x' (the percentage), we cross-multiply:
55.04 * 100 = 21.5 * x
5504 = 21.5x
x = 5504 / 21.5
x = 256
Thus, using the proportion method, we again find that 55.04 is 256% of 21.5.
Interpreting the Result: Understanding Percentages Greater Than 100%
It's important to note that the result, 256%, is greater than 100%. This indicates that the "part" (55.04) is larger than the "whole" (21.5). A percentage greater than 100% signifies that the part represents more than the entirety of the whole. This often occurs when dealing with growth, increases, or situations where the final value exceeds the initial value.
Practical Applications of Percentage Calculations
Percentage calculations are fundamental to many real-world applications. Here are a few examples:
-
Finance: Calculating interest rates, profit margins, discounts, tax rates, and investment returns all rely heavily on percentage calculations. Understanding percentages is crucial for making sound financial decisions.
-
Business: Analyzing sales figures, market share, growth rates, and cost-effectiveness all involve percentage calculations. Businesses use these calculations to track performance, identify trends, and make strategic decisions.
-
Science: In scientific research, percentages are used to represent data, express concentrations, and calculate statistical significance. Scientists use percentages to analyze experimental results and draw conclusions.
-
Everyday Life: Calculating tips, discounts, sales tax, and understanding nutritional information on food labels all require percentage calculations. These calculations help us make informed choices in our daily lives.
Advanced Percentage Calculations and Problem-Solving Techniques
While the basic percentage formula provides a solid foundation, several advanced techniques and problem-solving approaches can simplify complex percentage calculations.
Working with Decimals and Fractions
Percentages can be easily converted to decimals and fractions, offering alternative ways to approach problems. Remember:
- To convert a percentage to a decimal, divide the percentage by 100. For example, 25% = 25/100 = 0.25.
- To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.75 = 0.75 * 100 = 75%.
- To convert a fraction to a percentage, first convert the fraction to a decimal by dividing the numerator by the denominator, then multiply by 100. For example, 3/4 = 0.75 = 75%.
Solving for the Whole or the Part
The basic percentage formula can be rearranged to solve for the whole or the part, depending on the information provided:
-
Solving for the whole: If you know the percentage and the part, you can solve for the whole using the formula: Whole = (Part / Percentage) * 100
-
Solving for the part: If you know the percentage and the whole, you can solve for the part using the formula: Part = (Percentage / 100) * Whole
Percentage Increase and Decrease
Calculating percentage increases and decreases is crucial in various situations. The formulas are:
- Percentage Increase: [(New Value - Original Value) / Original Value] * 100
- Percentage Decrease: [(Original Value - New Value) / Original Value] * 100
Error Analysis and Avoiding Common Mistakes
Several common mistakes can occur when working with percentages. Being aware of these potential pitfalls can help you avoid errors:
-
Incorrect Formula Application: Ensure you are using the correct formula for the specific problem you're solving. Carefully identify the part, the whole, and the percentage.
-
Decimal Point Errors: Pay close attention to decimal points when performing calculations. A misplaced decimal point can significantly affect the result.
-
Misinterpretation of Percentages Greater Than 100%: Remember that percentages greater than 100% indicate that the part is larger than the whole.
-
Rounding Errors: Be mindful of rounding errors, especially when performing multiple calculations. Round off only at the final stage of the calculation to minimize error accumulation.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that empowers you to interpret data, make informed decisions, and solve real-world problems effectively. By understanding the fundamental concepts, utilizing various calculation methods, and being aware of potential errors, you can confidently tackle a wide range of percentage problems. Remember to always double-check your work and ensure that your results align with the context of the problem. The ability to accurately and efficiently calculate percentages is a cornerstone of numerical literacy and a vital asset in numerous academic and professional pursuits.
Latest Posts
Latest Posts
-
Which Conditions Create Snow Select Three Responses
Jun 06, 2025
-
Which Graph Is Defined By The Function Given Below
Jun 06, 2025
-
The Hierarchy Of Controls Specifies That Which Of The Following
Jun 06, 2025
-
Which Of The Following Is True About Temporary Stairs
Jun 06, 2025
-
24 Divided By 849 With Remainder
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 21.5 Is 55.04 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.