Which Expression Is Equivalent To 4y2 3 3y 2
Breaking News Today
Jun 06, 2025 · 4 min read
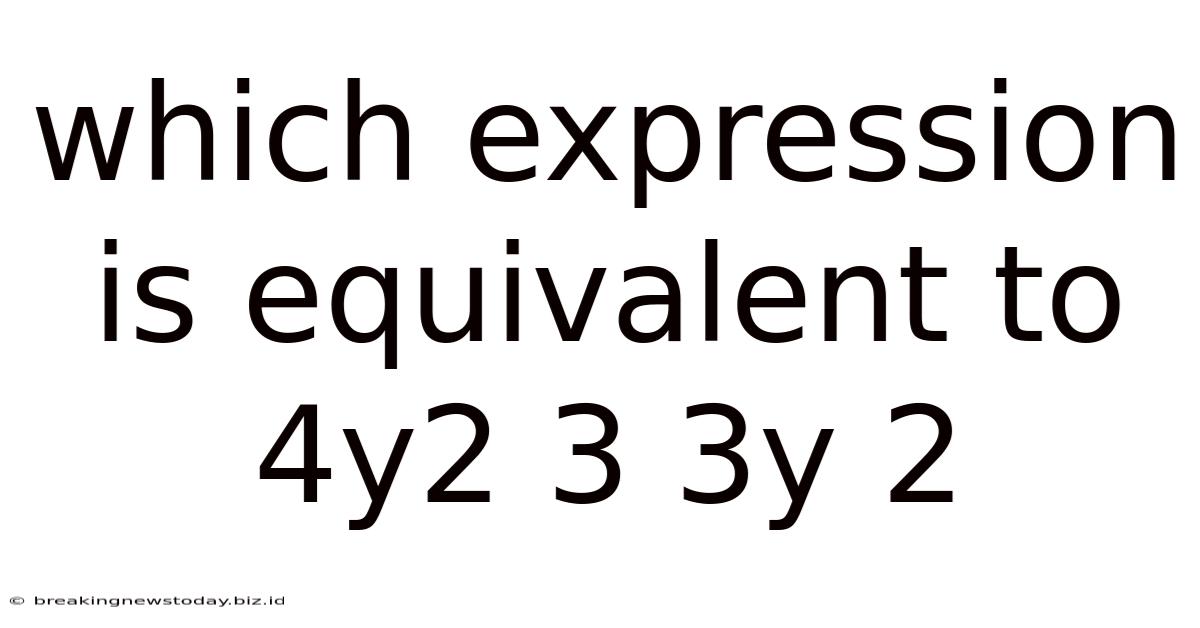
Table of Contents
Which Expression is Equivalent to 4y² + 3 – 3y²? A Deep Dive into Algebraic Simplification
Finding equivalent expressions is a fundamental skill in algebra. This seemingly simple problem – determining which expression is equivalent to 4y² + 3 – 3y² – unlocks a deeper understanding of combining like terms, simplifying expressions, and the fundamental principles of algebraic manipulation. This article will not only provide the solution but also explore the underlying concepts, offering various approaches and examples to solidify your understanding.
Understanding the Problem: 4y² + 3 – 3y²
The core of the problem lies in simplifying the given algebraic expression: 4y² + 3 – 3y². This involves identifying and combining like terms. Like terms are terms that have the same variables raised to the same powers. In this expression, we have:
- Like terms: 4y² and -3y² (both have the variable 'y' raised to the power of 2)
- Constant term: 3 (a term without a variable)
Simplifying the Expression: Step-by-Step Solution
To simplify the expression, we combine the like terms:
-
Identify like terms: We've already identified 4y² and -3y² as like terms.
-
Combine like terms: Add the coefficients (the numbers in front of the variables) of the like terms: 4 - 3 = 1. This means 4y² - 3y² = 1y², or simply y².
-
Rewrite the simplified expression: After combining the like terms, the expression becomes y² + 3.
Therefore, the simplified expression equivalent to 4y² + 3 – 3y² is y² + 3.
Different Approaches to Simplification
While the above method is the most straightforward, let's explore alternative approaches that reinforce the underlying concepts:
1. Using the Commutative Property
The commutative property of addition states that the order of terms doesn't affect the sum. We can rearrange the terms to group the like terms together before simplifying:
4y² + 3 – 3y² = 4y² – 3y² + 3 (Rearranging terms) = (4 - 3)y² + 3 (Combining coefficients) = y² + 3 (Simplified expression)
2. Visual Representation: Using Algebra Tiles
Algebra tiles are a visual tool that can help understand the concept of combining like terms. Each tile represents a term. For example:
- A large square could represent y².
- A small square could represent 1.
Using this representation, you would have four large squares (4y²), three small squares (3), and three negative large squares (-3y²). When you combine the positive and negative large squares, you are left with one large square (y²) and three small squares (3), visually representing y² + 3.
Common Mistakes to Avoid
Understanding common errors helps avoid pitfalls during algebraic simplification:
-
Ignoring signs: A common mistake is forgetting the sign of the coefficient. Always include the sign (+ or -) when combining like terms. For instance, not accounting for the negative sign in -3y² would lead to an incorrect result.
-
Incorrectly combining unlike terms: You cannot combine terms with different variables or the same variable raised to different powers. For example, you cannot simplify 2x² + 3x into 5x or 5x².
-
Misunderstanding exponents: Remember the rules of exponents. In this case, y² represents y multiplied by itself (y * y), and it's different from y or y³.
Expanding the Concept: More Complex Examples
Let's build upon this fundamental understanding by tackling slightly more complex examples:
Example 1: Simplify 5x² + 2x – 3x² + 7x – 4
-
Identify like terms: 5x² and -3x²; 2x and 7x; -4 (constant)
-
Combine like terms: (5 - 3)x² + (2 + 7)x – 4
-
Simplified expression: 2x² + 9x – 4
Example 2: Simplify 3a²b + 4ab² – a²b + 2ab²
-
Identify like terms: 3a²b and -a²b; 4ab² and 2ab²
-
Combine like terms: (3 - 1)a²b + (4 + 2)ab²
-
Simplified expression: 2a²b + 6ab²
These examples demonstrate that the fundamental principle of combining like terms remains consistent even when dealing with more complex expressions involving multiple variables.
Practical Applications: Where Equivalent Expressions Matter
The ability to simplify algebraic expressions is crucial in various fields:
-
Mathematics: Simplifying expressions is fundamental to solving equations, inequalities, and other mathematical problems.
-
Physics: Many physics formulas involve algebraic expressions that need to be simplified to solve for specific variables.
-
Engineering: Engineers use algebraic simplification extensively in designing and analyzing systems.
-
Computer Science: Simplifying expressions is essential in optimizing algorithms and improving program efficiency.
-
Finance: Algebraic expressions are used extensively in financial modeling and calculations.
Conclusion: Mastering Algebraic Simplification
The seemingly simple question of finding an equivalent expression for 4y² + 3 – 3y² offers a window into the broader world of algebraic manipulation. By understanding the concept of like terms, applying the commutative property, and practicing with different examples, you solidify a crucial skill applicable across various fields. Remember to carefully combine like terms, paying close attention to signs and exponents, to avoid common errors and achieve accurate simplification. The ability to confidently manipulate and simplify algebraic expressions is a cornerstone of mathematical literacy and problem-solving prowess. Through consistent practice and a solid grasp of fundamental principles, you will master this essential skill.
Latest Posts
Latest Posts
-
On The Number Line Below Length Ab
Jun 07, 2025
-
A Bicycle Tire Is 28 Inches In Diameter
Jun 07, 2025
-
Which Statement Accurately Describes The Rock Layers
Jun 07, 2025
-
Where Are The Asymptotes For The Following Function Located
Jun 07, 2025
-
Estimate The Sum Of 279 And 217
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To 4y2 3 3y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.