Which Expression Is Equivalent To 6x2-19x-55
Breaking News Today
Jun 08, 2025 · 4 min read
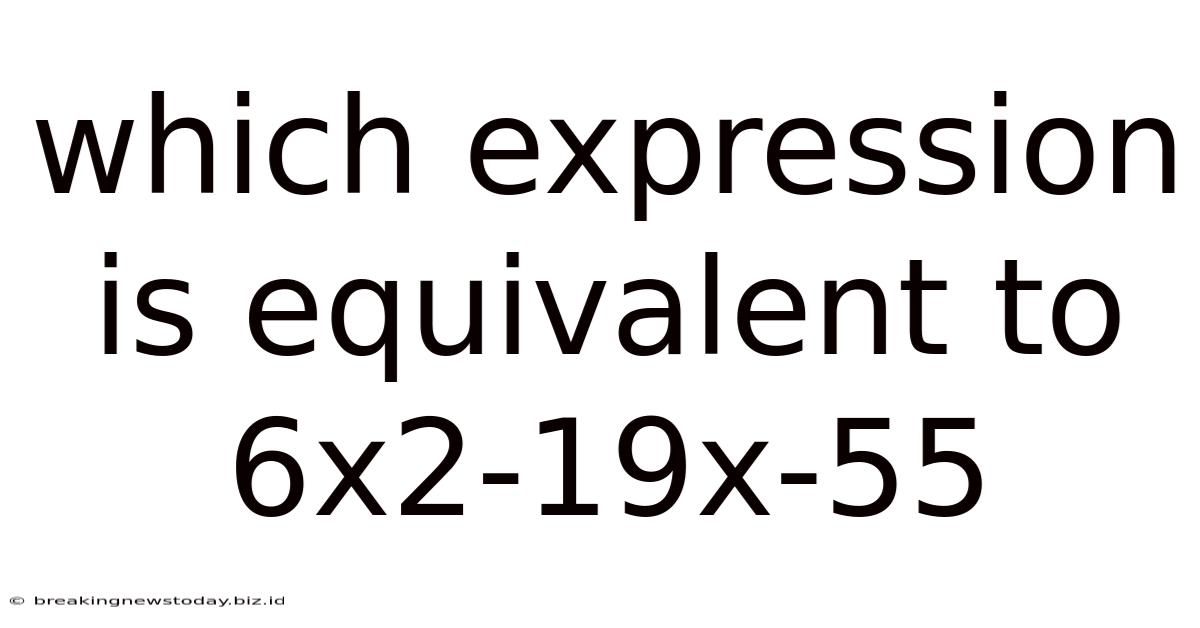
Table of Contents
Which Expression is Equivalent to 6x² - 19x - 55? A Comprehensive Guide to Factoring Quadratic Equations
Finding an equivalent expression for a quadratic equation like 6x² - 19x - 55 often involves factoring. This process breaks down the quadratic into a product of two simpler expressions, revealing the roots and providing a different, but mathematically identical, representation. This comprehensive guide will explore various methods for factoring this specific quadratic and explain the underlying mathematical principles. We'll also cover common mistakes to avoid and provide practice problems to solidify your understanding.
Understanding Quadratic Equations
Before diving into factoring 6x² - 19x - 55, let's refresh our understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is 2. The general form is:
ax² + bx + c = 0
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our target equation, 6x² - 19x - 55, fits this form, with a = 6, b = -19, and c = -55.
Methods for Factoring 6x² - 19x - 55
Several methods can be used to factor this quadratic expression. We'll explore the most common approaches:
1. The AC Method (Factoring by Grouping)
This method is particularly useful for quadratic equations where the coefficient of x² (a) is not 1. Here's how it works:
-
Find the product ac: In our case, ac = 6 * -55 = -330.
-
Find two numbers that multiply to ac and add to b: We need two numbers that multiply to -330 and add to -19. After some trial and error (or using a systematic approach), we find that -33 and 10 satisfy these conditions (-33 * 10 = -330 and -33 + 10 = -19).
-
Rewrite the middle term: Replace -19x with -33x + 10x:
6x² - 33x + 10x - 55
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
3x(2x - 11) + 5(2x - 11)
-
Factor out the common binomial: Notice that (2x - 11) is common to both terms. Factor it out:
(2x - 11)(3x + 5)
Therefore, the factored form of 6x² - 19x - 55 is (2x - 11)(3x + 5).
2. Using the Quadratic Formula
The quadratic formula provides a direct way to find the roots (solutions) of a quadratic equation. While it doesn't directly give the factored form, it can help us arrive at it. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in the values from our equation (a = 6, b = -19, c = -55):
x = [19 ± √((-19)² - 4 * 6 * -55)] / (2 * 6) x = [19 ± √(361 + 1320)] / 12 x = [19 ± √1681] / 12 x = [19 ± 41] / 12
This gives us two solutions:
x₁ = (19 + 41) / 12 = 60 / 12 = 5 x₂ = (19 - 41) / 12 = -22 / 12 = -11/6
These solutions represent the values of x that make the equation equal to zero. We can use these roots to construct the factored form:
(x - 5)(x + 11/6)
To eliminate the fraction, we multiply the entire expression by 6:
6(x - 5)(x + 11/6) = (6x - 30)(x + 11/6) = (2x - 11)(3x + 5)
This confirms the factored form we obtained using the AC method.
3. Trial and Error
For simpler quadratic equations, trial and error can be an effective method. You would try different combinations of binomial factors until you find one that multiplies to give the original quadratic. This method becomes less efficient as the coefficients become larger. For 6x² - 19x - 55, it would involve testing many combinations. While possible, the AC method or quadratic formula is generally preferred for efficiency.
Verifying the Factored Form
It's crucial to verify your factored form by expanding it back to the original quadratic expression. Let's expand (2x - 11)(3x + 5):
(2x - 11)(3x + 5) = 2x(3x) + 2x(5) - 11(3x) - 11(5) = 6x² + 10x - 33x - 55 = 6x² - 19x - 55
This confirms that our factored form is correct.
Common Mistakes to Avoid
- Incorrect signs: Pay close attention to the signs when factoring. A single incorrect sign will lead to an incorrect factorization.
- Incorrect GCF: Ensure you've factored out the greatest common factor correctly from each group when using the AC method.
- Not checking your answer: Always expand the factored form to verify it matches the original expression.
Practice Problems
Try factoring the following quadratic equations using the methods discussed above:
- x² + 5x + 6
- 2x² + 7x + 3
- 3x² - 10x + 8
- 4x² - 12x + 9
Remember to check your answers by expanding the factored forms.
Conclusion
Factoring quadratic equations is a fundamental skill in algebra. Understanding different methods like the AC method, using the quadratic formula, and even trial and error allows you to approach various quadratic expressions with confidence. Remember to always verify your results to ensure accuracy. Practice makes perfect, so keep working through problems to hone your factoring abilities. Mastering this skill will greatly assist you in solving more complex algebraic problems and advance your mathematical understanding.
Latest Posts
Latest Posts
-
The Highest Surface Wind Speeds Occur When There Is A
Jun 08, 2025
-
After The Resuscitation Event The Bls Team Conducted A Debriefing
Jun 08, 2025
-
In The Xy Plane A Circle Has Center C
Jun 08, 2025
-
65124 Rounded To The Nearest Thousand
Jun 08, 2025
-
Narration Is Similar To Other Types Of Writing Because
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To 6x2-19x-55 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.