Which Expression Is Equivalent To 8x-12y+32
Breaking News Today
Jun 04, 2025 · 5 min read
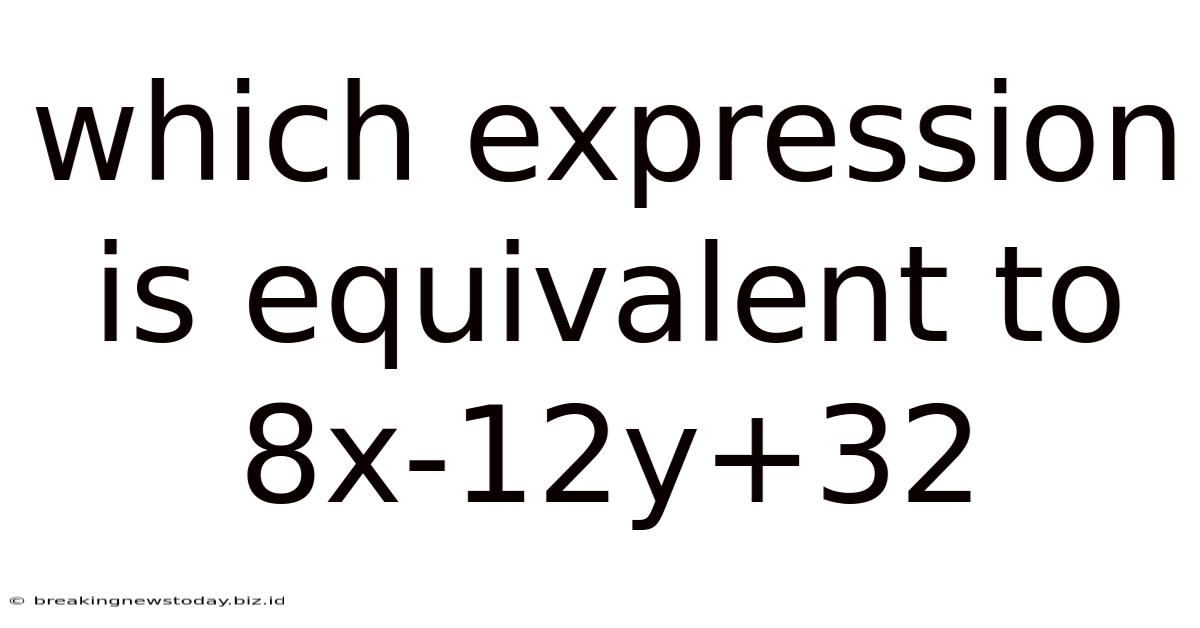
Table of Contents
Which Expression is Equivalent to 8x - 12y + 32? A Comprehensive Guide to Simplifying Algebraic Expressions
Finding equivalent expressions is a fundamental skill in algebra. This seemingly simple task—determining which expression is equivalent to 8x - 12y + 32—underpins a deeper understanding of algebraic manipulation and simplification. This comprehensive guide will not only answer the question directly but also explore the underlying principles, providing you with the tools to tackle similar problems with confidence.
Understanding Equivalent Expressions
Before diving into the specifics of 8x - 12y + 32, let's establish a clear understanding of what constitutes equivalent expressions. Two expressions are considered equivalent if they produce the same result for all possible values of their variables. This means that no matter what numbers you substitute for 'x' and 'y', the equivalent expressions will always yield the identical numerical outcome.
This equivalence is achieved through algebraic manipulation, primarily involving the properties of real numbers:
- Commutative Property: The order of addition or multiplication does not affect the result. For example, a + b = b + a and ab = ba.
- Associative Property: The grouping of terms in addition or multiplication does not affect the result. For example, (a + b) + c = a + (b + c) and (ab)c = a(bc).
- Distributive Property: Multiplication distributes over addition (and subtraction). For example, a(b + c) = ab + ac and a(b - c) = ab - ac.
These properties are the cornerstone of simplifying and manipulating algebraic expressions, allowing us to rewrite them in different but equivalent forms.
Factoring: The Key to Finding Equivalent Expressions
The most common method for finding equivalent expressions is factoring. Factoring involves expressing an expression as a product of simpler expressions. In the context of 8x - 12y + 32, we look for common factors among the terms.
Notice that each term (8x, -12y, and 32) is divisible by 4:
- 8x = 4 * 2x
- -12y = 4 * (-3y)
- 32 = 4 * 8
Using the distributive property in reverse, we can factor out the common factor of 4:
8x - 12y + 32 = 4(2x - 3y + 8)
Therefore, 4(2x - 3y + 8) is an equivalent expression to 8x - 12y + 32.
Exploring Other Potential Equivalent Expressions (Advanced Concepts)
While 4(2x - 3y + 8) is the most straightforward equivalent expression obtained through simple factoring, it's important to understand that other, more complex manipulations could potentially lead to equivalent expressions. However, these would likely involve more advanced techniques and wouldn't necessarily be considered "simpler" forms.
For instance, consider the concept of expanding expressions:
Let's say we have the expression 4(2x - 3y) + 32. Expanding this expression using the distributive property gives us:
4(2x) - 4(3y) + 32 = 8x - 12y + 32
This demonstrates that 4(2x - 3y) + 32 is also equivalent to our original expression.
Similarly, we could introduce other variables or constants, creating more complex yet equivalent expressions. The key is that these expressions, when simplified, would ultimately reduce back to 8x - 12y + 32.
This highlights the richness and flexibility of algebraic manipulation. While one equivalent expression might be preferable in certain contexts (usually the simplest factored form), many other equivalent forms are possible.
Why is Finding Equivalent Expressions Important?
The ability to find equivalent expressions is crucial for several reasons:
-
Simplification: Equivalent expressions allow us to simplify complex expressions into more manageable forms. This makes calculations easier and helps in understanding the underlying relationships between variables.
-
Problem Solving: Many mathematical problems require manipulating expressions to isolate variables or solve equations. Finding equivalent expressions is essential for these manipulations.
-
Proofs and Theorems: In more advanced mathematics, proving theorems often involves transforming expressions into equivalent forms to demonstrate relationships and equalities.
-
Computer Programming: Computer programs often rely on algebraic manipulation to optimize calculations and enhance efficiency.
Practical Application: Solving Equations
Let's see how finding equivalent expressions can be applied practically in solving equations. Suppose we have the equation:
8x - 12y + 32 = 0
We can use the equivalent expression we found earlier to simplify this equation:
4(2x - 3y + 8) = 0
Dividing both sides by 4, we get:
2x - 3y + 8 = 0
This simplified equation is much easier to work with when solving for 'x' or 'y' (depending on the context of the problem).
Common Mistakes to Avoid
When working with equivalent expressions, be mindful of these common mistakes:
-
Incorrect application of the distributive property: Remember to distribute the factor to every term inside the parentheses.
-
Errors in signs: Pay close attention to positive and negative signs when factoring or expanding expressions. A simple sign error can lead to an incorrect equivalent expression.
-
Confusing factoring with division: Factoring involves finding common factors and expressing the expression as a product. Dividing by a common factor produces a different result and does not yield an equivalent expression in the same sense.
Practice Problems
To solidify your understanding, try finding equivalent expressions for the following:
- 6a + 9b - 15
- 10x - 25y + 5z
- -4p + 8q - 12r + 16
Remember to use the distributive property and look for common factors among the terms. Check your answers by expanding your factored expressions to verify they return to the original expressions.
Conclusion: Mastering Equivalent Expressions
Finding equivalent expressions is a foundational skill in algebra. Through understanding and applying the properties of real numbers, particularly the distributive property, we can simplify complex expressions and solve equations effectively. Mastering this skill will significantly enhance your ability to manipulate algebraic expressions and will be invaluable as you progress in your mathematical journey. The ability to efficiently identify and manipulate equivalent expressions lays the groundwork for more advanced algebraic concepts and problem-solving techniques. Consistent practice and attention to detail are key to achieving proficiency in this crucial area of algebra. Remember to always check your work and verify that your equivalent expression produces the same result as the original expression for all possible values of the variables involved.
Latest Posts
Latest Posts
-
All Of The Following Are Examples Of Self Discipline Except
Jun 06, 2025
-
All Cultures Have Developed A Unique Interdependent Relationship With Their
Jun 06, 2025
-
Costs For Fuel Oil And Tires Are Examples Of
Jun 06, 2025
-
Cones And Polyhedrons Both Have Only One Base
Jun 06, 2025
-
Which Of The Following Best Describes Perpendicular Lines
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To 8x-12y+32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.