Which Expressions Are Equivalent To 4d+6+2d
Breaking News Today
Jun 06, 2025 · 5 min read
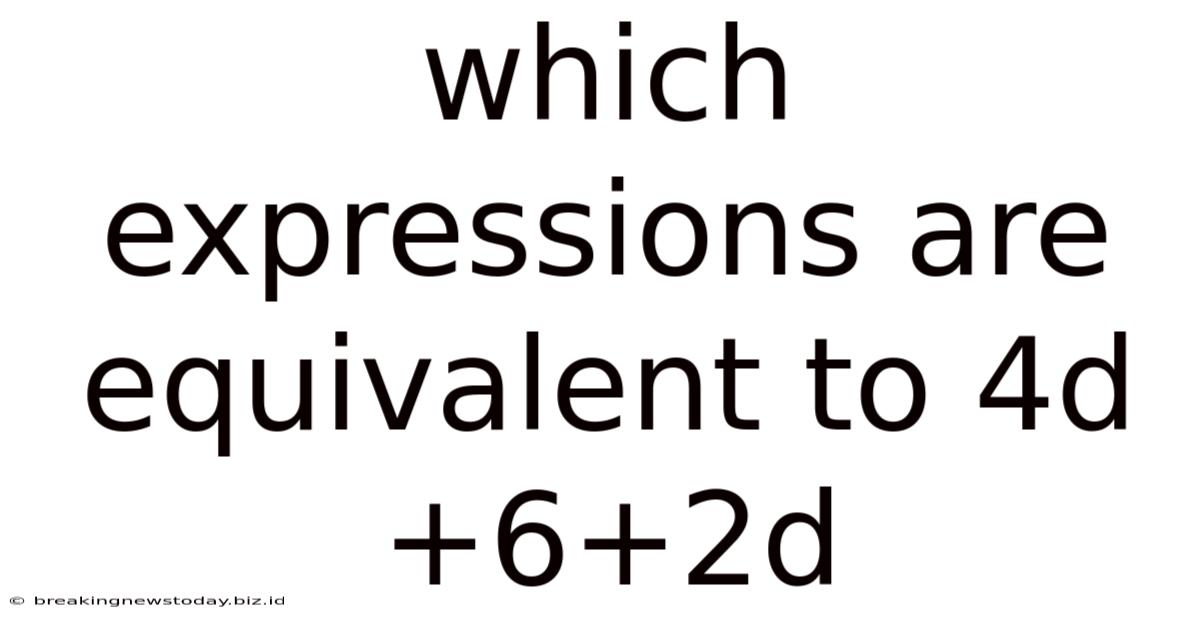
Table of Contents
Which Expressions Are Equivalent to 4d + 6 + 2d? A Comprehensive Guide
Understanding algebraic expressions and their equivalencies is fundamental to success in algebra and beyond. This article delves deep into the expression 4d + 6 + 2d, exploring various equivalent expressions and the underlying principles of simplification and manipulation. We will cover different methods, provide numerous examples, and even touch upon the practical applications of these concepts.
Understanding the Expression 4d + 6 + 2d
Before we jump into finding equivalent expressions, let's analyze the given expression: 4d + 6 + 2d. This is a simple algebraic expression containing:
- Variables: The letter 'd' represents a variable, meaning it can hold different numerical values.
- Coefficients: The numbers 4 and 2 are coefficients, multiplying the variable 'd'.
- Constant: The number 6 is a constant; its value remains unchanged.
The expression represents a combination of a variable term (terms with 'd') and a constant term. Our goal is to find other ways to write this expression while maintaining its mathematical value.
Simplifying the Expression: The Foundation of Equivalence
The most straightforward way to find equivalent expressions is to simplify the original expression. This involves combining like terms, which are terms that contain the same variable raised to the same power. In our case, the like terms are 4d and 2d.
Step 1: Combine like terms
4d + 2d = 6d
Step 2: Rewrite the expression
The simplified expression becomes: 6d + 6
Therefore, 6d + 6 is a simplified, and thus equivalent, expression to 4d + 6 + 2d. This is the most basic and often the most useful equivalent expression.
Generating More Equivalent Expressions: The Art of Manipulation
While simplification provides one equivalent, we can generate numerous others through algebraic manipulation. These manipulations involve applying the properties of equality – adding, subtracting, multiplying, or dividing both sides of an equation by the same non-zero value – to create new, but equivalent, expressions. However, since we're dealing with an expression rather than an equation, we'll focus on transformations that don't alter the expression's inherent value.
Introducing Parentheses: Grouping for Clarity and Complexity
Parentheses can be strategically used to group terms without changing the value. However, remember the order of operations (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right).
Here are some examples of equivalent expressions using parentheses:
- (4d + 2d) + 6: This groups the like terms before simplification.
- 4d + (6 + 2d): This groups the constant and one variable term.
- (4d + 6 + 2d): While seemingly redundant, this demonstrates that the entire original expression itself is equivalent.
These examples highlight how parentheses can be used to structure the expression differently, creating alternative forms without affecting its mathematical value.
Using the Distributive Property: A Powerful Tool
The distributive property (a(b + c) = ab + ac) allows us to expand or factor expressions, leading to new equivalent forms. While it's not directly applicable to our simplified form (6d + 6), we can apply it to the original expression if we manipulate it slightly.
Let's factor out a 2 from the variable terms:
2(2d + d) + 6
This, after simplification within the parentheses becomes:
2(3d) + 6 = 6d + 6 – again, our simplified form.
While this example didn't create a vastly different expression, the distributive property is crucial when dealing with more complex expressions.
Adding and Subtracting Zero: A Clever Trick
Adding or subtracting zero doesn't alter the expression's value. This might seem trivial, but it's a powerful technique for generating equivalent expressions. For example:
- 6d + 6 + 0: This is clearly equivalent.
- 6d + 6 + 3d - 3d: This adds and subtracts the same variable term, leaving the value unchanged. The advantage here is that the expression has become slightly more complex.
- 6d + 6 + 5 - 5: Adding and subtracting a constant also maintains equivalence.
This method offers a way to create more complex-looking equivalent expressions while maintaining their mathematical integrity.
Multiplying and Dividing by One: Maintaining the Balance
Similar to adding zero, multiplying or dividing by one doesn't alter the expression's value. This provides another way to generate numerous equivalent expressions:
- (6d + 6) * 1: Multiplication by one.
- (6d + 6) / 1: Division by one.
- (6d + 6) * (x/x): Multiplying by a fraction equal to one (where 'x' is any non-zero number).
While these examples might appear trivial, the principle is essential for understanding more complex algebraic manipulations.
Beyond Simplification: The Importance of Equivalent Expressions
Understanding that several expressions can be equivalent to a single expression is crucial for:
- Problem Solving: Different forms of an expression might be more suitable for solving specific problems.
- Equation Solving: Manipulating expressions into equivalent forms simplifies equation-solving techniques.
- Mathematical Reasoning: The ability to recognize equivalent expressions underpins a deeper understanding of algebraic concepts.
- Advanced Algebra: Techniques for generating equivalent expressions are fundamental in more advanced algebraic topics.
Practical Applications and Real-World Examples
Equivalent expressions are not just abstract concepts. They are vital tools in numerous real-world scenarios:
- Calculating Areas and Volumes: Formulas for areas or volumes can often be expressed in equivalent forms, simplifying calculations based on the available data.
- Financial Modeling: In finance, expressions representing profits, losses, or investments might be manipulated into equivalent forms to facilitate comparisons or analysis.
- Engineering and Physics: Equivalent expressions are essential in simplifying equations describing physical phenomena.
- Computer Programming: Efficient algorithms often involve manipulating expressions to optimize performance.
Conclusion: Mastering Equivalent Expressions
Mastering the art of finding equivalent expressions is a cornerstone of algebraic proficiency. This skill goes beyond simple simplification. It encompasses a deeper understanding of algebraic properties, allowing for manipulation and transformation to suit the context of a given problem. The techniques discussed – simplification, using parentheses, the distributive property, adding/subtracting zero, and multiplying/dividing by one – provide a robust toolkit for generating numerous equivalent expressions for any given algebraic expression, including the expression 4d + 6 + 2d. The ability to recognize and generate equivalent expressions is an invaluable tool for problem-solving and a testament to a strong grasp of algebraic principles. Remember to practice consistently to build your proficiency in these essential algebraic techniques.
Latest Posts
Latest Posts
-
What Are The Missing Angle Measures In Parallelogram Rstu
Jun 07, 2025
-
At Which Location Would An Objects Weight Be The Greatest
Jun 07, 2025
-
0 291 Rounded To The Nearest Hundredth
Jun 07, 2025
-
Cold Food Can Be Held Intentionally Without Temperature Control For
Jun 07, 2025
-
In Cell E15 Enter A Formula To Find The Lowest
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Which Expressions Are Equivalent To 4d+6+2d . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.