Which Graph Represents The Inequality 3y 5x 6
Breaking News Today
Jun 06, 2025 · 5 min read
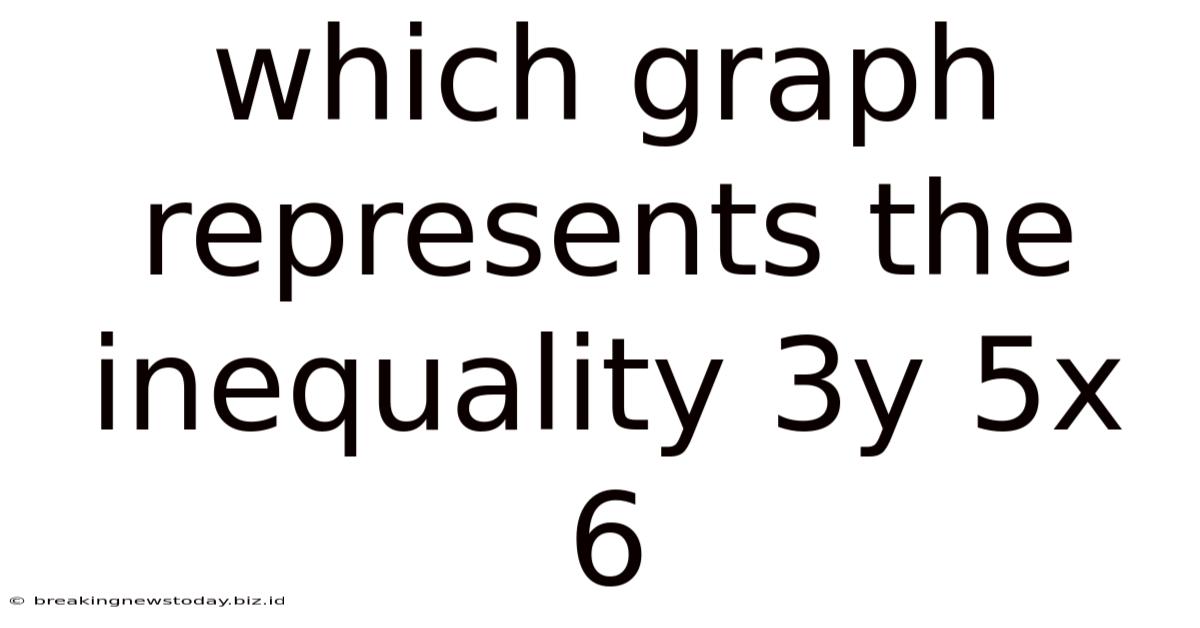
Table of Contents
Which Graph Represents the Inequality 3y ≤ 5x + 6? A Comprehensive Guide
Understanding how to represent inequalities graphically is a crucial skill in algebra. This guide will walk you through the process of identifying the correct graph for the inequality 3y ≤ 5x + 6, explaining the steps involved and providing a clear understanding of the underlying concepts. We'll cover graphing linear inequalities, interpreting the inequality symbol, and handling boundary lines. By the end, you'll be able to confidently graph similar inequalities and understand their visual representations.
Understanding Linear Inequalities
Before diving into the specific inequality, let's establish a foundational understanding of linear inequalities. A linear inequality is a mathematical statement that compares two expressions using inequality symbols: < (less than), > (greater than), ≤ (less than or equal to), or ≥ (greater than or equal to). Unlike equations, which have a single solution, inequalities typically have a range of solutions. These solutions can be represented graphically as a shaded region on a coordinate plane.
A linear inequality involves a linear expression, meaning the variables have an exponent of 1. The general form of a linear inequality in two variables (x and y) is:
Ax + By ≤ C or Ax + By < C or Ax + By ≥ C or Ax + By > C
where A, B, and C are constants.
Steps to Graphing 3y ≤ 5x + 6
To graph the inequality 3y ≤ 5x + 6, we'll follow these systematic steps:
Step 1: Rewrite the Inequality in Slope-Intercept Form
The slope-intercept form of a linear equation is y = mx + b, where 'm' is the slope and 'b' is the y-intercept. While we're dealing with an inequality, rewriting it in this form makes graphing much easier.
Let's manipulate 3y ≤ 5x + 6:
- Divide by 3:
y ≤ (5/3)x + 2
Now we have the inequality in slope-intercept form. The slope (m) is 5/3, and the y-intercept (b) is 2.
Step 2: Graph the Boundary Line
The boundary line represents the equation y = (5/3)x + 2. This line separates the coordinate plane into two regions. Because our inequality includes "≤" (less than or equal to), the boundary line itself is included in the solution set. Therefore, we graph it as a solid line.
To graph the line:
- Plot the y-intercept: The y-intercept is (0, 2). Plot this point on the y-axis.
- Use the slope to find another point: The slope is 5/3, which means for every 3 units you move to the right on the x-axis, you move 5 units up on the y-axis. Starting from the y-intercept (0, 2), move 3 units to the right and 5 units up. This gives you the point (3, 7).
- Draw the line: Draw a solid straight line through the points (0, 2) and (3, 7). Extend the line in both directions across the coordinate plane.
Step 3: Choose a Test Point
To determine which region of the coordinate plane satisfies the inequality, choose a test point that is not on the boundary line. The origin (0, 0) is often the easiest point to use, unless the boundary line passes through the origin.
Step 4: Test the Inequality
Substitute the coordinates of your test point (0, 0) into the inequality y ≤ (5/3)x + 2:
0 ≤ (5/3)(0) + 2
0 ≤ 2
This statement is true.
Step 5: Shade the Solution Region
Since the test point (0, 0) satisfies the inequality, the region containing (0, 0) is the solution region. Shade this region on the graph. This shaded region represents all the points (x, y) that satisfy the inequality 3y ≤ 5x + 6.
Interpreting the Graph
The graph should show a solid line representing y = (5/3)x + 2, with the region below the line shaded. Any point within the shaded region, including points on the solid line itself, represents a solution to the inequality 3y ≤ 5x + 6. Points above the line are not solutions.
Common Mistakes to Avoid
- Incorrect line type: Remember to use a solid line for inequalities with "≤" or "≥" and a dashed line for inequalities with "<" or ">".
- Shading the wrong region: Always test a point not on the line to determine which side to shade.
- Misinterpreting the slope and y-intercept: Double-check your calculations when rewriting the inequality into slope-intercept form.
Advanced Concepts and Extensions
This foundational understanding allows you to explore more complex scenarios:
- Systems of Inequalities: Graphing multiple inequalities simultaneously can help solve real-world problems with multiple constraints. The solution region would be the area where all shaded regions overlap.
- Nonlinear Inequalities: Inequalities involving quadratic or other non-linear expressions require different graphing techniques but follow similar principles of boundary lines and test points.
- Applications in Real-World Problems: Linear inequalities are used extensively in optimization problems, resource allocation, and constraint modeling across various fields.
Conclusion
Graphing linear inequalities is a fundamental skill in algebra with wide-ranging applications. By carefully following the steps outlined in this guide, you can confidently represent linear inequalities graphically, understanding their meaning and implications. Remember to practice consistently to build your proficiency and explore more advanced topics. Through mastering this fundamental skill, you’ll be well-equipped to tackle more challenging mathematical concepts and real-world applications. Remember to always check your work and ensure your graph accurately reflects the given inequality. Good luck, and happy graphing!
Latest Posts
Latest Posts
-
Select The Definite Article That Corresponds To Each Noun
Jun 06, 2025
-
Which Statement Best Explains How The Excerpt Exemplifies Elizabethan Drama
Jun 06, 2025
-
The Upper Half Of An Oblong Shape Is The
Jun 06, 2025
-
6 1 Reteach To Build Understanding Answer Key
Jun 06, 2025
-
What Is The Solubility Of Kcl At 5 C
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Which Graph Represents The Inequality 3y 5x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.