Which Graph Represents Y 1 2 X 2
Breaking News Today
Jun 06, 2025 · 5 min read
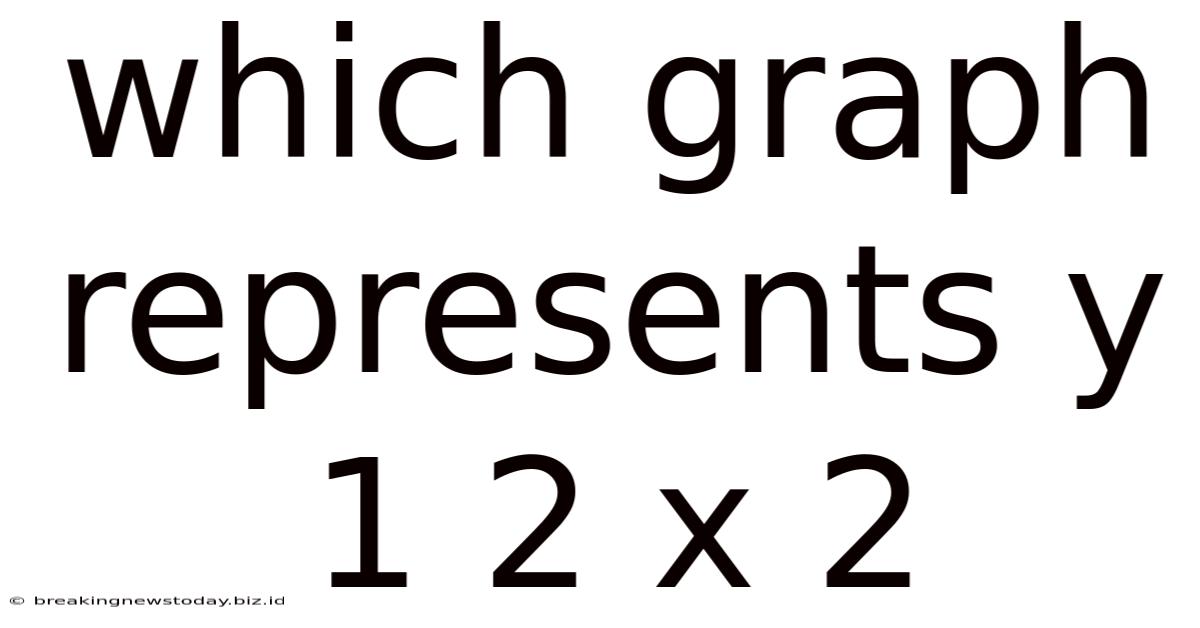
Table of Contents
Which Graph Represents y = 1/2x²? A Comprehensive Guide
Understanding how to visually represent mathematical functions is crucial in various fields, from engineering and physics to economics and data science. This article delves into the specifics of the quadratic function y = 1/2x², exploring its properties, its graphical representation, and how it compares to other quadratic functions. We'll also touch upon practical applications and how to effectively communicate this information visually.
Understanding the Equation y = 1/2x²
The equation y = 1/2x² represents a parabola, a specific type of curve. Let's break down the components:
-
x²: This term indicates that the function is quadratic, meaning the highest power of x is 2. Quadratic functions always produce parabolic curves.
-
1/2: This is the coefficient of the x² term. It's also known as the vertical scaling factor. This factor determines how "wide" or "narrow" the parabola will be. A coefficient greater than 1 will make the parabola narrower, while a coefficient between 0 and 1 will make it wider. In this case, the 1/2 coefficient stretches the parabola vertically.
-
y: This represents the dependent variable, whose value depends on the value of x.
Key Characteristics of the Parabola y = 1/2x²
Before visualizing the graph, let's identify some key features of this parabola:
-
Vertex: The vertex is the lowest (or highest, for a parabola that opens downwards) point on the parabola. For y = 1/2x², the vertex is at the origin (0,0). This is because when x = 0, y = 0.
-
Axis of Symmetry: The parabola is symmetrical about a vertical line passing through its vertex. The axis of symmetry for y = 1/2x² is the y-axis (x = 0). Points equidistant from the y-axis will have the same y-value.
-
Concavity: The parabola opens upwards because the coefficient of the x² term (1/2) is positive. If the coefficient were negative, the parabola would open downwards.
-
Shape: As mentioned earlier, the 1/2 coefficient makes the parabola wider than the standard parabola y = x². The parabola y = x² is considered the "parent" function for all quadratic functions of the form y = ax².
-
x-intercept and y-intercept: The x-intercept is where the graph intersects the x-axis (where y = 0). In this case, the only x-intercept is at (0, 0). The y-intercept is where the graph intersects the y-axis (where x = 0), also at (0, 0).
Graphing y = 1/2x²
To accurately graph y = 1/2x², you can use several methods:
-
Plotting Points: Choose several x-values, substitute them into the equation to calculate the corresponding y-values, and plot these points on a Cartesian coordinate system. Connect the points to form a smooth curve. For example:
- If x = -2, y = 1/2(-2)² = 2
- If x = -1, y = 1/2(-1)² = 0.5
- If x = 0, y = 1/2(0)² = 0
- If x = 1, y = 1/2(1)² = 0.5
- If x = 2, y = 1/2(2)² = 2
-
Using Graphing Software or Calculators: Many graphing calculators and software programs (like Desmos, GeoGebra, etc.) can directly plot this function. Simply input the equation, and the program will generate the graph. This is often the most efficient and accurate method, especially for more complex functions.
-
Understanding Transformations: You can visualize the graph by understanding how it relates to the parent function y = x². The 1/2 coefficient represents a vertical compression (or stretching, depending on the value). This means the parabola y = 1/2x² is a wider version of y = x².
Comparing y = 1/2x² to Other Quadratic Functions
Let's compare y = 1/2x² to other parabolas to highlight the effect of the coefficient:
-
y = x²: This is the standard parabola, narrower than y = 1/2x².
-
y = 2x²: This parabola is narrower than both y = x² and y = 1/2x².
-
y = -1/2x²: This parabola opens downwards, unlike y = 1/2x², which opens upwards. The shape is identical to y = 1/2x², but reflected across the x-axis.
-
y = 1/2x² + 2: This parabola is identical in shape to y = 1/2x², but shifted vertically upward by 2 units. The vertex is at (0, 2).
-
y = 1/2(x - 1)²: This parabola is identical in shape to y = 1/2x², but shifted horizontally to the right by 1 unit. The vertex is at (1, 0).
Practical Applications of y = 1/2x²
The parabola represented by y = 1/2x², and quadratic functions in general, have numerous applications in various fields:
-
Physics: Describing projectile motion (e.g., the trajectory of a ball thrown upwards).
-
Engineering: Designing parabolic antennas and reflectors, as these shapes efficiently focus energy (light or radio waves).
-
Architecture: Creating parabolic arches for structural support.
-
Economics: Modeling cost functions and revenue curves.
-
Computer Graphics: Generating curves and shapes for animations and visual effects.
Communicating the Graph Effectively
When presenting the graph of y = 1/2x², ensure clarity and accuracy:
-
Label Axes: Clearly label the x-axis and y-axis with appropriate units.
-
Scale: Choose a scale that accurately represents the data and allows the parabola's shape to be clearly seen.
-
Title: Provide a descriptive title, such as "Graph of y = 1/2x²".
-
Key Features: Highlight the vertex, axis of symmetry, and any intercepts. You might even add these features as annotations on the graph itself.
Conclusion
The graph of y = 1/2x² is a specific type of parabola with a vertex at the origin, opening upwards, and wider than the standard parabola y = x². Understanding its characteristics and how it relates to other quadratic functions is essential for interpreting and applying mathematical models in various real-world scenarios. By accurately graphing and effectively communicating this information, you can ensure clear understanding and effective application in any field. Remember to use appropriate tools and techniques to create visually appealing and informative representations of the function. The combination of theoretical understanding and skillful visual representation is key to mastering quadratic functions and their applications.
Latest Posts
Latest Posts
-
How Many Atoms Are Present In 179 0 G Of Iridium
Jun 06, 2025
-
Match Each Property Of A Liquid To What It Indicates
Jun 06, 2025
-
Which Delivery System Requires Friction To Release The Performance Ingredients
Jun 06, 2025
-
Unit 8 Quadratic Equations Homework 1 Answer Key
Jun 06, 2025
-
Which Of The Following Has Uniform Stress
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Which Graph Represents Y 1 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.