Which Is Equivalent To 80 1/4x
Breaking News Today
Jun 08, 2025 · 5 min read
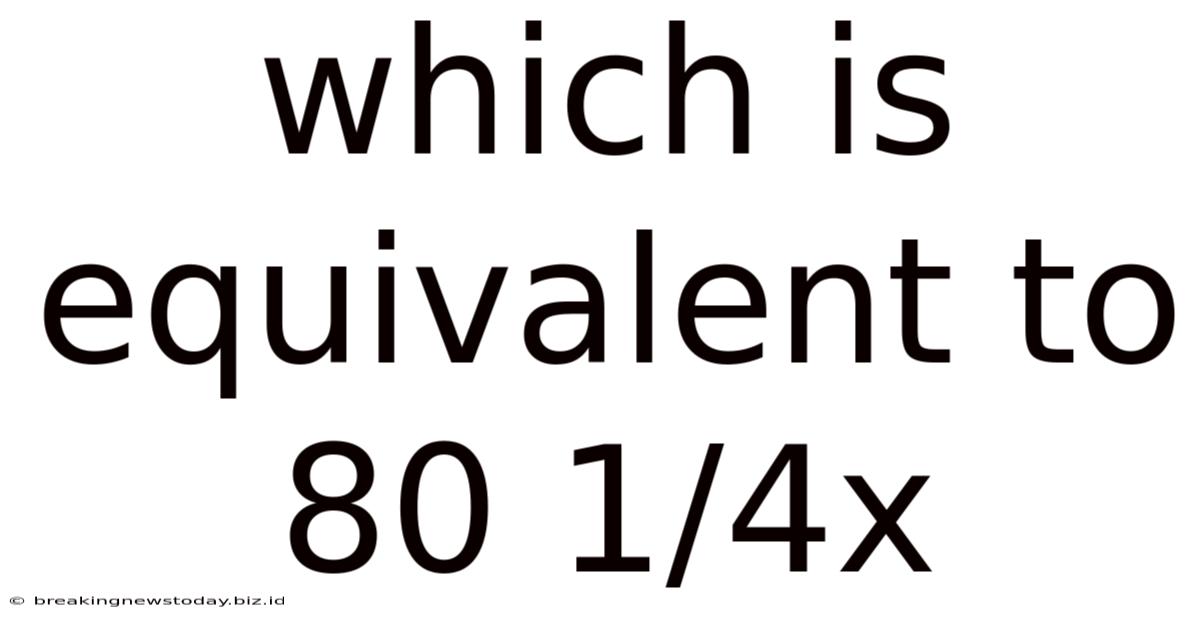
Table of Contents
Decoding the Mystery: What's Equivalent to 80 ¼ x?
This seemingly simple question, "What's equivalent to 80 ¼ x?", opens a door to a fascinating world of mathematical equivalence and its practical applications. While the immediate answer might seem straightforward – it's simply 80.25x – the true depth lies in understanding why this is the case and how this principle applies across various fields. This article delves into the intricacies of fractional equivalents, exploring their representation, manipulation, and significance in diverse contexts, ultimately providing a comprehensive understanding of the equivalence of 80 ¼ x.
Understanding Fractional Equivalents
The core concept here rests on our understanding of fractions and their decimal counterparts. A fraction represents a part of a whole. In the expression 80 ¼ x, ¼ represents one-quarter, or 0.25 in decimal form. Therefore, 80 ¼ x is essentially 80 + ¼ x, which translates directly to 80 + 0.25x. Combining these terms gives us the equivalent expression: 80.25x.
This simple conversion highlights the fundamental principle of equivalence in mathematics: different expressions can represent the same value. This principle holds true regardless of whether we're dealing with simple algebraic expressions like this one or more complex mathematical equations.
Practical Applications: Beyond the Basics
The seemingly simple conversion from 80 ¼ x to 80.25x has profound implications across numerous fields. Let's explore a few:
1. Engineering and Construction
In engineering and construction, precision is paramount. Dealing with measurements and calculations involving fractions is commonplace. Converting fractions to decimals allows for easier calculations using digital tools and ensures consistent precision.
Imagine calculating the amount of material needed for a project. If you require 80 ¼ lengths of a particular pipe, expressing this as 80.25 lengths simplifies calculations when using computerized inventory management systems or when calculating total costs based on unit prices. The precision avoids potential errors that could arise from working directly with fractions.
2. Finance and Accounting
Financial calculations often involve fractions, especially when dealing with interest rates, stock prices, or unit costs. Converting fractions to decimals streamlines calculations and improves accuracy, making financial modeling and forecasting more efficient.
Consider calculating compound interest. An annual interest rate of 80 ¼ percent is easily converted to 80.25 percent for simpler computational purposes in spreadsheet software or financial calculators. This ensures accurate calculations of investment returns or loan payments.
3. Data Analysis and Statistics
In data analysis and statistics, dealing with fractional data points is very common. Converting fractions to decimals allows for smoother integration into statistical software packages and simplifies data manipulation for analysis.
For example, if you are analyzing survey data and have responses with fractional values (e.g., 80 ¼ hours of work per week), converting these fractions to decimals simplifies data processing for generating statistical summaries like mean, median, and standard deviation.
4. Software Development and Programming
In programming, precision in numerical calculations is crucial. Many programming languages handle decimal numbers more efficiently than fractions, leading to faster and more optimized code.
Converting 80 ¼ to 80.25 enhances the efficiency of numerical calculations in algorithms, particularly in situations demanding high-speed data processing. This ensures programs run smoothly and provide accurate results.
Beyond the Numerical: Understanding Context
While the numerical conversion is straightforward, the significance of the expression 80 ¼ x depends heavily on its context. The "x" variable represents an unknown quantity. The value of the entire expression – 80.25x – is directly proportional to the value of "x."
This proportionality is crucial in various applications. For example:
-
Scaling: If 'x' represents a unit of measurement (e.g., meters, kilograms, or dollars), then 80.25x indicates a scaled quantity. Doubling the value of 'x' will double the value of the entire expression.
-
Variables in Equations: In algebraic equations, 80.25x might represent a component of a larger equation. Understanding the equivalence with 80 ¼ x is vital for simplifying and solving the equation.
-
Real-World Quantities: In real-world scenarios, 'x' could represent any quantifiable element. Accurate conversion to decimal form ensures clarity and precision in calculations relating to that element.
Expanding the Scope: Working with More Complex Fractions
The principle of converting fractions to decimals extends beyond simple fractions like ¼. Understanding how to handle more complex fractions is essential for broader mathematical proficiency.
For instance, consider the expression 80 3/8 x. To convert this to a decimal equivalent, we first convert the fraction 3/8 to its decimal form (3 ÷ 8 = 0.375). Therefore, 80 3/8 x is equivalent to 80.375x. This process involves dividing the numerator by the denominator and then adding the result to the whole number.
Similarly, any fractional component within a mathematical expression can be converted to its decimal form using this principle. This simplifies calculations and improves the precision of results, irrespective of the complexity of the fraction.
Advanced Considerations: Rounding and Precision
In practical applications, rounding off decimal equivalents might be necessary. The level of precision required depends entirely on the context of the problem.
For example, in financial calculations, high precision is generally needed. Rounding to several decimal places might be required to avoid significant errors in final results. However, in less sensitive applications, rounding to fewer decimal places might suffice.
The choice to round and the number of decimal places retained should always be made judiciously, considering the potential impact on the final results. Improper rounding can lead to significant errors, especially in scenarios requiring high levels of accuracy.
Conclusion: The Importance of Equivalent Expressions
Understanding the equivalence between 80 ¼ x and 80.25x is more than just a simple mathematical conversion. It represents a fundamental concept with far-reaching applications across various fields. The ability to seamlessly translate between fractional and decimal representations enhances calculation efficiency, improves precision, and ensures the accuracy of results in diverse contexts. Whether it's in engineering, finance, data analysis, or software development, mastering this conversion remains a cornerstone of numerical proficiency. This skill facilitates clear communication, efficient problem-solving, and reliable results in a world increasingly reliant on precise numerical computations. The simple act of converting 80 ¼ x to 80.25x unlocks a gateway to a deeper understanding of mathematical equivalence and its practical significance.
Latest Posts
Latest Posts
-
Event 2 Has A Causal Relationship With Event 1 When
Jun 08, 2025
-
Farming Requires Space So It Primarily Contributes To
Jun 08, 2025
-
If Two Lemons Cost 15 Cents
Jun 08, 2025
-
Which Sentences Contain Pronoun Shifts Check All That Apply
Jun 08, 2025
-
A Non Moving Pickup Or Sedan
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Which Is Equivalent To 80 1/4x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.