Which Is The Correct Graph Of The Inequality Y 2x+1
Breaking News Today
Jun 06, 2025 · 5 min read
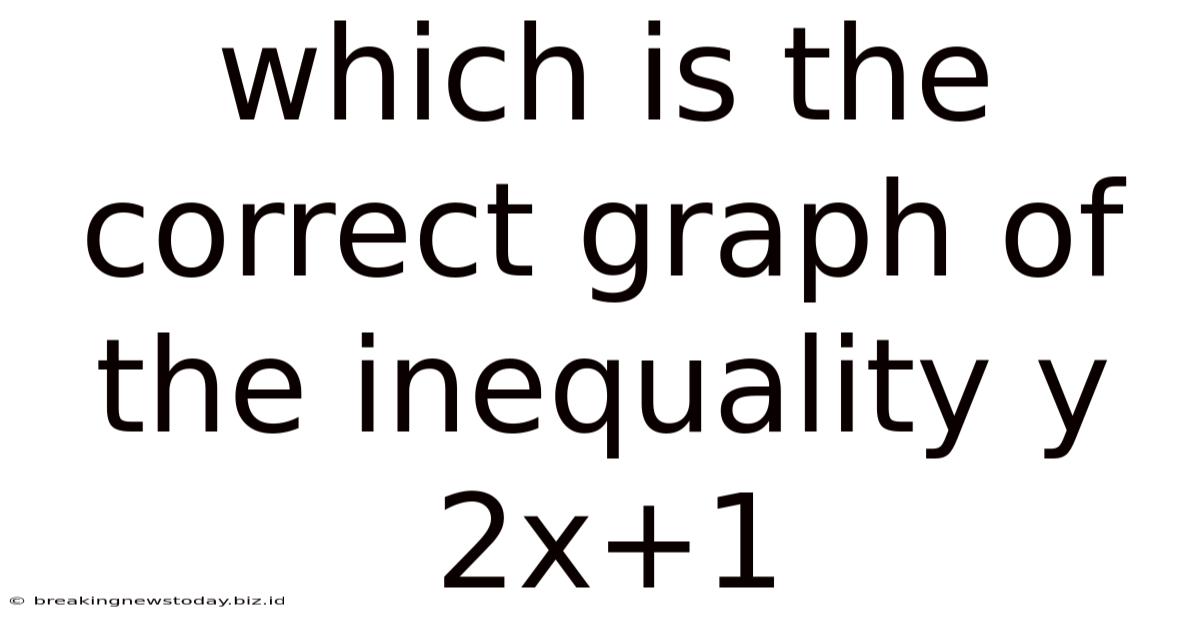
Table of Contents
Which is the Correct Graph of the Inequality y ≥ 2x + 1? A Comprehensive Guide
Understanding how to graph linear inequalities is crucial for success in algebra and beyond. This guide will walk you through the process of graphing the inequality y ≥ 2x + 1, explaining the steps involved and clarifying common misconceptions. We'll delve into the intricacies of shading, boundary lines, and how to interpret the solution set. By the end, you'll be confident in graphing similar inequalities and understanding what the graph represents.
Understanding Linear Inequalities
Before we tackle the specific inequality y ≥ 2x + 1, let's review the fundamental concepts of linear inequalities. A linear inequality is a mathematical statement that compares two expressions using inequality symbols such as:
- ≥: greater than or equal to
- >: greater than
- ≤: less than or equal to
- <: less than
Unlike linear equations, which have a single solution, linear inequalities have an infinite number of solutions. These solutions are typically represented graphically as a shaded region on a coordinate plane.
Graphing the Inequality: A Step-by-Step Guide
To graph y ≥ 2x + 1, we follow these steps:
Step 1: Graph the Boundary Line
First, we treat the inequality as an equation: y = 2x + 1. This equation represents a straight line. We can graph this line using two methods:
-
Using the slope-intercept form: The equation is already in slope-intercept form (y = mx + b), where 'm' is the slope (2 in this case) and 'b' is the y-intercept (1). Plot the y-intercept (0, 1) on the y-axis. From this point, use the slope to find another point. A slope of 2 means for every 1 unit increase in x, y increases by 2 units. So, from (0, 1), move one unit right and two units up to reach the point (1, 3). Draw a line through these two points.
-
Using the x and y-intercepts: To find the x-intercept, set y = 0 and solve for x: 0 = 2x + 1 => x = -1/2. The x-intercept is (-1/2, 0). We already know the y-intercept is (0, 1). Plot these points and draw a line through them.
Crucial Note: Because the inequality includes "≥" (greater than or equal to), the boundary line should be solid. This signifies that the points on the line are included in the solution set. If the inequality were y > 2x + 1 or y < 2x + 1, the boundary line would be dashed to indicate that the points on the line are not part of the solution.
Step 2: Determine the Shaded Region
Now, we need to determine which side of the line represents the solution set. The inequality y ≥ 2x + 1 indicates that we are looking for all points where the y-coordinate is greater than or equal to the expression 2x + 1.
To find the shaded region, we can use a test point. A convenient test point is the origin (0, 0). Substitute the coordinates of the origin into the inequality:
0 ≥ 2(0) + 1 0 ≥ 1
This statement is false. Since the test point (0, 0) does not satisfy the inequality, we shade the region that does not contain the origin. This means we shade the region above the line.
Step 3: Interpreting the Graph
The shaded region represents the solution set of the inequality y ≥ 2x + 1. Any point within this shaded region (including the points on the solid line) will satisfy the inequality. Any point outside the shaded region will not satisfy the inequality.
Common Mistakes to Avoid
- Incorrect Boundary Line: Failing to draw a solid line for "≥" or "≤" inequalities, or drawing a solid line for ">" or "<" inequalities.
- Incorrect Shading: Shading the wrong region due to an incorrect test point or misunderstanding of the inequality symbol.
- Ignoring the Equality Part: Forgetting that the points on the line are included in the solution set when using "≥" or "≤".
- Misinterpreting the Slope: Incorrectly using the slope to plot points, leading to an incorrectly drawn line.
Practical Applications and Extensions
Understanding linear inequalities has widespread applications in various fields:
-
Resource Allocation: In business, linear inequalities can model constraints in resource allocation problems, helping determine the optimal combination of resources to maximize profit or minimize costs. For example, if
xrepresents the number of units of product A andyrepresents the number of units of product B, an inequality likey ≥ 2x + 1could represent a minimum production requirement. -
Optimization Problems: Linear programming, a powerful technique used in operations research, relies heavily on linear inequalities to define constraints and find optimal solutions.
-
Economics: In economics, linear inequalities can be used to model budget constraints or production possibilities.
Advanced Concepts: Systems of Linear Inequalities
The concepts we’ve discussed extend to systems of linear inequalities, which involve multiple inequalities. Graphing a system of inequalities involves graphing each inequality individually and then identifying the region where all the inequalities are satisfied simultaneously. This region is often referred to as the "feasible region" and is crucial in optimization problems.
Conclusion: Mastering Linear Inequality Graphs
Graphing linear inequalities like y ≥ 2x + 1 is a fundamental skill in algebra. By carefully following the steps outlined above – graphing the boundary line correctly, choosing an appropriate test point to determine the shaded region, and understanding the meaning of the inequality symbols – you can confidently graph any linear inequality and interpret its solution set. Remember to practice regularly to solidify your understanding and build your problem-solving skills. This knowledge forms a solid foundation for tackling more complex mathematical concepts and real-world applications.
Latest Posts
Latest Posts
-
Which Statement About Credit For A Clep Exam Is True
Jun 07, 2025
-
Will The Product Help Me Live An Opulent Lifestyle
Jun 07, 2025
-
Which Transformation Maps The Pre Image To The Image
Jun 07, 2025
-
Drop Cup And Pint Are Measurements In Which System
Jun 07, 2025
-
Which Formula Stands For Boric Acid
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Which Is The Correct Graph Of The Inequality Y 2x+1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.